(学习笔记)十大经典算法——K-means聚类算法
概述
聚类算法是在无监督的情况下将对象自动分组的一种分析方法,典型的聚类算法分为三个阶段:特征选择和特征提取,数据对象间相似度计算,根据相似度将数据对象分组。聚类算法的目标是将数据集合分成若干簇,使得同一簇内的数据点相似度尽可能大,而不同簇间的数据点相似度尽可能小。可分为层次聚类算法和划分聚类算法。
常见的聚类算法有k-means,STING,CLIQUE等。本文所记录的K-means算法是由J.B.MacQueen在1967年提出的,也有一种说法是该算法由Steinhaus1955年、Lloyd1957年、Ball&Hall1965年、McQueen1967年分别在各自领域独自提出的。是数据挖掘中的一种重要的分析方法,是无监督学习算法,属于一种划分聚类算法,广泛应用于机器学习等领域,十大经典数据挖掘算法之一。
优点
运算简单、效果好、容易实现,适于处理大规模数据,可伸缩性强,时间复杂度接近线性。
缺点
算法中聚类数目K值难以确定,初始聚类中心如何选取,离群点的检测与取出,距离和相似性度量等,对噪声数据和离群点数据较为敏感,对于大数据量算法的开销较大。
应用
广泛应用于文档聚类、市场细分、图像分割、特征学习等。
原理
MacQueen的思想为:给定n个数据点{x1,x2,xn},找到K个聚类中心{a1,a2,ak},使得每个数据点与它最近的聚类中心得距离平方和最小,并将这个距离平方和称之为目标函数,为 W n = ∑ i = 1 n min 1 ≤ j ≤ k ∣ x i − a j ∣ 2 W_n=\sum_{i=1}^{n}{\min_{1\le j\le k}{|x_i-a_j|}^2} Wn=∑i=1nmin1≤j≤k∣xi−aj∣2 ,后来随着研究的深入,该算法诸多问题便显露出来,主要有需要预先确定K值,会受到初始聚类中心影响,难以处理分类属性数据以及容易收敛于局部最优解等。用欧式距离(Wn)作为衡量数据对象间相似度的标准,相似度与数据对象间的距离成反比,相似度越大,距离越小。
算法步骤:
输入:K(簇的数目),D(包含n个对象的数据集)。
输出:K个簇的集合。
步骤:
- 从D中任意选取K个对象作为初始簇中心;
- repeat,循环步骤3-5;
- 根据簇中对象的均值,将每个对象指派到最相似的簇;
- 更新簇均值,即计算每个蔟中对象的均值, x i ˉ = ∑ x ∈ D i x / ∣ D i ∣ \bar{x_i}=\sum_{x\in D_i}{x/|D_i|} xiˉ=∑x∈Dix/∣Di∣ 此处Di为簇内数据集合;
- until目标函数不再发生变化,即 W n = ∑ i = 1 k ∑ x ∈ D i ∣ x − x i ˉ ∣ 2 W_n=\sum_{i=1}^{k}\sum_{x\in D_i}{|x-\bar{x_i}|}^2 Wn=∑i=1k∑x∈Di∣x−xiˉ∣2 不再发生明显变化。
步骤5返回步骤3循环执行,当目标函数不再发生变化时算法结束。

该图片截取自引文[2]
发展方向:
提升K-means算法处理海量或多维数据集的能力。如何将算法更好地用于处理指数级数据的聚类,也是需要研究的方向。
降低K-means算法的时间复杂度。如何能更好更快地提升聚类能力,需要做更进一步的优化。
优化
算法优化主要从以下几个方面进行,几十年来改进方法层出不群,本文只挑几个比较典型容易理解的改进方法作为特例。
聚类收敛条件: 针对于会陷入局部最优解,1995年Chinrungrueng等人提出了改进算法,在原有的算法中加入了两种新的机制分别为:允许算法在自适应过程中摆脱目标函数Wn的干扰;采用反馈方式,根据当前聚类质量动态的调整算法的收敛速度。后来学界中采用类内紧密型和类间分散性的比值来作为收敛函数,这样当收敛函数收敛到极小值时,类内紧密型和类间分散性都可以达到较优值。
K值的选取: 研究发现K值的选取在 [ 2 , N ] [2,\sqrt N] [2,N] ,N为数据空间中所有数据点的个数。解决方案有基于聚类有效函数的解决方法、基于遗传算法的解决方法、以及其他解决方案。最有代表性的选取方法是令K逐渐增加,直到K=N,在此过程中目标函数Wn回单调减少,而当K增加到一定数值时减少速度会减慢,直到K=N时为零 ,此时意味着各点自成一组。由此递减曲线出现的拐点可作为最优的K值。
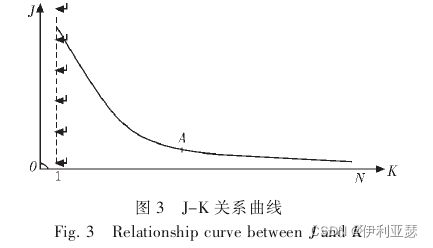
该图片截取自引文[7]
初始聚类中心的选择: 在算法中,初始聚类中心是随机选取的,因此可能造成在同一类别的样本被强行当做两个类的初始聚类中心,使聚类结果最终只能收敛于局部最优解,因此算法的聚类效果很大程度上依赖于初始聚类中心的选择。针对该问题学界就基于密度、基于优化算法的解决方案以及其他解决方案。
处理分类属性数据: 传统的算法只适用于处理数值属性的数据,而对于分类属性和混合属性数据集则不太适用。基于此Huang提出了适用于纯分类属性数据集的K-modes算法和适用于混合属性数据集的K-prototypes算法。后来,Chaturvedi等提出面向分类数据集的K-modes-CGC算法。蒋盛益等人认为K-modes算法采用modes来表示累的对应“中心”,难以反映类中对象的取值情况,会导致距离计算不够准确,从而影响聚类质量,基于此提出了k-summary算法。
离群点去除: 传统去除方法主要是通过计算欧氏距离,去除离其他点距离之和最远的 λ \lambda λ%(人为设定)个点。还有一种基于密度的离群点的检测算法就是首先根据LOF算法计算每一个数据对象的离群因子,离群因子越大说明该数据对象偏离中心的程度越大,越有可能是离群点。选出最小的前a*n(a由人为设定)个数据对象作为候选聚类中心样本,再使用最大最小法选出K个初始聚类中心,进行K-means迭代输出聚类结果。最大最小法即为选取所有数据点到聚类中心的欧式距离的最小值,然后在这些最小值中选取最大值作为聚类中心点。
其他方面改进: 最近几年出现了遗传算法、粒子群算法、萤火虫算法、蚁群算法等与传统的K-means算法相结合的改进算法,这几类算法的共同点是具有一定的全局优化能力,理论上可以在一定时间内找到最优解或近似最优解。
算法
算法代码python和matlab均可实现,笔者没有代码基础也不会写,只能参考其他博主代码。
参考文献
[1] 董文静. K-means算法综述 [J]. 信息与电脑(理论版), 2021, 33(11): 76-8.
[2] 杨俊闯, 赵超. K-Means聚类算法研究综述 [J]. 计算机工程与应用, 2019, 55(23): 7-14+63.
[3] 丛思安, 王星星. K-means算法研究综述 [J]. 电子技术与软件工程, 2018, (17): 155-6.
[4] 吴进宝. K-means算法研究综述 [J]. 电子技术与软件工程, 2014, (18): 207.
[5] 李卫军. K-means聚类算法的研究综述 [J]. 现代计算机(专业版), 2014, (23): 31-2+6.
[6] 周爱武, 陈宝楼, 王琰. K-Means算法的研究与改进 [J]. 计算机技术与发展, 2012, 22(10): 101-4.
[7] 王千, 王成, 冯振元, et al. K-means聚类算法研究综述 [J]. 电子设计工程, 2012, 20(07): 21-4.
[8] 吴夙慧, 成颖, 郑彦宁, et al. K-means算法研究综述 [J]. 现代图书情报技术, 2011, (05): 28-35.