论文《Session-based Recommendation with Graph Neural Networks》阅读

论文概况

本文是2019年AAAI上的一篇论文，聚焦于使用图神经网络解决序列化推荐问题，提出了SRGNN（Session-based Recommendation with Graph Neural Networks）模型。

Introduction

作者提出了几个问题

• 一般在一段会话中不会包含很多的用户行为，而传统的推荐方法依赖于足够的用户-项目交互，这导致这些方法效果不佳。同时，一些方法将RNN的隐向量作为用户兴趣表征，然而在推荐系统中，会话大多数是匿名且碎片化的（数量很多但容量很小）
• 以往的研究表明，会话内物品的转换模式是非常重要的，但现有方法之研究了单向转换，而没有考虑到上下文之间的转换，距离较远的物品之间的相互作用。

对于上述问题，作者提出了SRGNN模型：（1）将离散的会话序列转化为图结构信息来捕获完整的物品转化模式。（2）使用最后一个物品的向量作为用户的兴趣进行会话嵌入

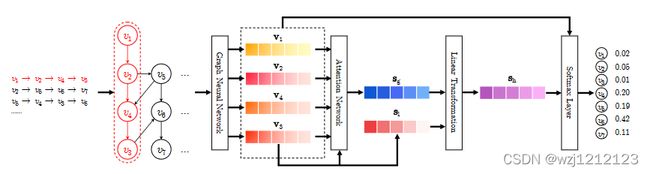
Method

A.Constructing Session Graphs

一个会话构建一个会话图，会话图中边的权重直接取决于该点所连接的点的数量，一个点的所有边权重和为1。根据会话图可以得到出度矩阵和入度矩阵。

B.Learning Item Embeddings on Session Graphs

下面根据会话图进行物品向量计算，SRGNN认为一个结点的向量与邻接节点向量和自己本身向量有关。首先根据各个节点的向量与节点之间的邻接关系进行聚合。
$${\mathbf{a}}_{s,i}^t={\mathbf{A}}_{s,i:}{\left[{\mathbf{v}}_1^{t-1},\dots ,{\mathbf{v}}_n^{t-1}\right]}^{\top }\mathbf{H}+\mathbf{b}\text{\hspace{1em}(1)}$$
之后计算重置门和更新门，利用循环门控单元来更新节点向量。
$${\mathbf{z}}_{s,i}^t=\sigma \left({\mathbf{W}}_z{\mathbf{a}}_{s,i}^t+{\mathbf{U}}_z{\mathbf{v}}_i^{t-1}\right)\text{\hspace{1em}(2)}$$
$${\mathbf{r}}_{s,i}^t=\sigma \left({\mathbf{W}}_r{\mathbf{a}}_{s,i}^t+{\mathbf{U}}_r{\mathbf{v}}_i^{t-1}\right)\text{\hspace{1em}(3)}$$
$${\mathbf{v}}_i^t=\tanh \left({\mathbf{W}}_o{\mathbf{a}}_{s,i}^t+{\mathbf{U}}_o\left({\mathbf{r}}_{s,i}^t\odot {\mathbf{v}}_i^{t-1}\right)\right)\text{\hspace{1em}(4)}$$
$${\mathbf{v}}_i^t=\left(1-{\mathbf{z}}_{s,i}^t\right)\odot {\mathbf{v}}_i^{t-1}+{\mathbf{z}}_{s,i}^t\odot {\mathbf{v}}_i^t\text{\hspace{1em}(5)}$$

C.Generating Session Embeddings

利用注意力机制将最后一个物品当作用户当前兴趣，生成整个会话的会话嵌入。
$${\alpha }_i={\mathbf{q}}^{\top }\sigma \left({\mathbf{W}}_1{\mathbf{v}}_n+{\mathbf{W}}_2{\mathbf{v}}_i+\mathbf{c}\right)\text{\hspace{1em}(6)}$$
$${\mathbf{s}}_{\mathrm{g}}=\sum _{i=1}^n{\alpha }_i{\mathbf{v}}_i\text{\hspace{1em}(7)}$$
将得到的长期兴趣与当前兴趣拼接再降维。
$${\mathrm{s}}_{\mathrm{h}}={\mathrm{W}}_3\left[{\mathrm{s}}_{\mathrm{l}};{\mathrm{s}}_{\mathrm{g}}\right]\text{\hspace{1em}(8)}$$

D.Making Recommendation and Model Training

将得到的会话嵌入与物品向量做乘积，再通过softmax得到推荐结果
$${\hat{\mathbf{z}}}_i={\mathbf{s}}_{\mathrm{h}}^{\top }{\mathbf{v}}_i\text{\hspace{1em}(9)}$$
$$\hat{\mathbf{y}}=\mathrm{softmax}(\hat{\mathbf{z}})\text{\hspace{1em}(10)}$$
使用交叉熵定义损失函数
$$\hat{\mathbf{y}}=\mathrm{softmax}(\hat{\mathbf{z}})\mathcal{L}(\hat{\mathbf{y}})=-\sum _{i=1}^m{\mathbf{y}}_i\log \left({\hat{\mathbf{y}}}_i\right)+\left(1-{\mathbf{y}}_i\right)\log \left(1-{\hat{\mathbf{y}}}_i\right)\text{\hspace{1em}(11)}$$

总结

SRGNN弥补了传统方法的不足之处，将GNN引入会话推荐，许多更为有效的模型都是在SRGNN基础上改进而来的。但SRGNN没有解决GNN本身的缺陷，比如过渡平滑问题。