实时高清渲染:全局光照(Global Illumination)[2]---漫反射/高光全局光照
目录
漫反射全局光照:
表面的预计算光照:
定向表面预光照:
预计算转移(PRT):
存储格式:
动态漫反射全局光照:
RSM:
LPV:
基本步骤:
步骤1简述:
步骤2简述:
步骤3简述:
步骤4简述:
基于体素的方法:
VXGI:
屏幕空间方法:
高光全局光照:
IBL:
split sum approximation:
预滤波环境贴图:
预计算BRDF:
基于体素的方法:
平面反射:
屏幕空间的方法:
SSR:
学习资料:
全局光照[1]导航:
实时高清渲染:全局光照(Global Illumination)[1]_This is MX的博客-CSDN博客_实时全局光照![]() https://blog.csdn.net/m0_56399931/article/details/123302771
https://blog.csdn.net/m0_56399931/article/details/123302771
前记:前面opengl的文章内容可能得晚些更新了,因为有些效果在bgfx上面实现了,不适合放带代码了-------------------------------------------------------------------------------------------------------------博主:mx
漫反射全局光照:
表面的预计算光照:
预先计算的辐照度值通常与漫反射颜色或反照率映射相乘,存储在一个单独的纹理集。虽然从理论上讲,出射度(辐照度时间漫反射颜色)可以预先计算并存储在一组纹理中,但在大多数情况下,许多实际考虑排除了这种选择。颜色映射通常是相当高的频率,它们利用各种各样的平铺,并且它们的部分经常在模型中重复使用,所有这些都是为了保持合理的内存使用。辐照度值通常要低得多,而且不容易重复使用。将光照和表面颜色分开会消耗更少的内存。
除了最严格的硬件平台外,现在很少使用预先计算的辐照度。根据定义,辐照度是针对给定法线方向计算的,因此我们不能使用法线映射来提供高频细节。这也意味着辐照度只能为平面预先计算。如果我们需要在动态几何上使用烘焙照明,我们需要其他方法来存储它。这些限制促使人们寻找使用定向组件存储预计算光照的方法。
定向表面预光照:
最常用的方法是存储完整的球面辐照度信息,例如使用球面谐波。该方案首先由Good和Taylor在加速光子映射的背景下提出,并由Shopf等人在实时环境中使用。在这两种情况下,定向辐照被存储在纹理中。如果使用9个球面谐波系数(三阶SH),质量很好,但存储和带宽成本较高。使用4个系数(二阶SH)成本更低,但很多细微之处会丢失,光照对比度更低,法线贴图也不太明显。Chen使用了Halo方法的一种变体,这种方法是为了以更低的成本获得三级SH的质量而开发的。他从球面信号中提取出最主要的光,并分别以颜色和方向的形式存储。剩余部分用二阶SH编码。这将系数的数量从27减少到18,质量损失很小。Hu描述了如何进一步压缩这些数据。Chen和Tatarchuk提供了他们在生产中使用的基于gpu的烘烤管道的进一步信息。Habel等人提出的h基是另一种解决方案。由于它只编码半球面信号,较少的系数就可以提供与球面谐波相同的精度。仅用6个系数就可以获得与三阶SH相当的质量。因为基只定义在一个半球上,我们需要在这个表面上的一些局部坐标系来正确地定位它。通常,由uu、参数化产生的切线帧用于此目的。如果将h基分量存储在纹理中,其分辨率应该足够高,以适应底层切线空间的变化。如果多个具有显著不同切线空间的三角形覆盖同一像素,重建信号将不精确。
球面谐波和h偏移的一个问题是它们都表现出ringing现象。虽然预过滤可以减轻这种效果,但它也可以平滑照明,这可能并不总是理想的。此外,即使是成本较低的变体,在存储和计算方面也有相对较高的成本。在更严格的情况下,如在低端平台或在虚拟现实渲染时,这种费用可能是令人望而却步的。成本是简单的替代方案仍然流行的原因。《半衰期2》使用自定义的半球形基础,存储三个颜色值,每个样本总共9个系数。环境/高光/方向(AHD)为基础的布局也是一个流行的选择,尽管它很简单。它已经被用于《使命召唤》系列和《最后生还者》等游戏中。参见图11.23。Crytek在《孤岛惊魂》中使用了这种变体。Crytek表示法由切线空间的平均光方向、平均光色和标量方向因子组成。最后一个值用于混合环境和方向组件,它们都使用相同的颜色。这将每个样本的存储系数减少到6个:三个值用于颜色,两个值用于方向,一个用于方向因子。Unity引擎也在其中一个模式中使用类似的方法。这种类型的表示是非线性的,这意味着,技术上,线性插值单个组件,无论是在像素还是顶点之间,都不是数学正确的。
如果我们需要关于任意方向照明的信息,而不仅仅是在表面上的一个半球内(例如,为动态几何提供间接照明),我们可以使用编码完整球面信号的方法。球面谐波在这里是很自然的。当内存不太受关注时,三阶SH(每个颜色通道9个系数)是最受欢迎的选择;否则,使用二阶(每个颜色通道4个系数,这匹配RGBA纹理中的组件数量,所以一个地图可以存储一个颜色通道的系数)。球面高斯也适用于全球面,因为波瓣可以分布在整个球面上,也可以只分布在法线周围的半球上。环境立方体贴图也是一个可行的选择。
预计算转移(PRT):
如果我们假设场景的几何形状没有变化,只改变了灯光,我们就可以预先计算光线如何与模型交互。 物体间的效果,如相互反射或次表面散射,可以预先分析到一定程度,并将结果存储起来,而无需对实际radiance值进行操作。 将入射光线转化为整个场景中radiance分布的描述的函数称为传递函数。 预先计算传递这个的解决方案称为预先计算传递或预计算radiance传递(PRT)方法。
PRT通常采用球谐函数来存储数据,球面谐波(Spherical Harmonics,简称SH)基函数是一组定义在球面上基函数。每个SH基函数由伴随勒让德多项式给出。
SH基函数具备一个的良好性质:正交完备性,不同的基函数之间相互正交,即有:
任何一个关于三维方向ω的函数f(ω)都可以转换成球面函数,该函数在SH基函数Bi(ω)下的权重计算(即投影)公式为:
投影之后,再用ci权重带入如下公式
可以对原始函数f(ω)进行复原,这个过程我们称之为重建。
我们来看反射方程:
我们把L(i)展开,记为:
把V(i)ρ(i,o)max(0,n⋅i)展开记为:
带回反射方程,得到:
再根据正交完备性,上述式子可以简化为:
这下我们轻而易举的知道,如果我们能够计算出li和ti,那么反射方程结果就是这两个乘积的和。
对于l和t的计算:
l的计算如下:
t的计算如下:
对于diffuse的BRDF,其本身与ωo无关,因此ωo无论如何变化,在预计算阶段我们都可以直接忽略。但如果是glossy材质,fr是会随着观察视角ωo的变化而变化的!为此,对于glossy材质的BRDF,我们写成如下形式:
即对于glossy材质,我们需要增加一个变量ωo进行打表。遍历ωo的离散取值,为每一个不同的ωo生成一个light transport向量t(ωo),因此glossy材质的tt是一个矩阵,矩阵规模为m×n,其中m是SH基函数个数,n是ωo离散化个数。对于glossy材质,计算最终的光照辐射率时是l向量和t矩阵的矩阵向量乘。
存储格式:
光照贴图是存储预计算光照最常见的方法之一。 存储特定类型的数据时也称为irradiance贴图,光照贴图被用来统称所有这些数据。 在运行时,GPU的内置纹理机制将会被使用。 通常是GPU中的值都是双线性过滤的,对于某些表示可能不是完全正确的。 例如,当使用AHD表示时,滤波后的D(方向)分量在插值后将不再是单位长度,因此需要进行重新归一化。 使用插值还意味着A(环境值)和H(高光值)并不完全是我们在采样点直接计算的结果。 也就是说,结果通常看起来是可以接受的,即使表示是非线性的。
在大多数情况下,光照贴图不能使用mipmapping,因为光贴图的分辨率比典型的反照率贴图或法线贴图小。 即使在高质量的应用中,一个光贴图的纹素至少可以覆盖大约20× 20厘米的面积,通常还会更多。 使用这种尺寸的像素,额外的mip级别几乎是不需要的。
为了在纹理中存储光照信息,物体需要提供一个独特的参数。当将漫反射颜色纹理映射到一个模型上时,通常网格的不同部分使用相同的纹理区域是很好的,特别是当一个模型的纹理具有一般的重复模式时。光照贴图重用是非常困难的,光照对于网格上的每个点都是独特的,所以每个三角形都需要在光照地图上占据自己独特的区域。创建参数化的过程从将网格分割成更小的块开始, 这既可以使用一些启发式自动完成,也可以使用工具手动完成。通常情况下,已经存在于其他纹理映射中的分割被使用。接下来,对每个chunk进行独立参数化,确保其各部分在纹理空间中不重叠,纹理空间中生成的元素称为图表(charts)或壳(shells), 最后,所有图表都打包到一个共同的纹理中,如下图:
光线被baking到一个场景中,光照贴图应用到表面上。 光照贴图使用一种独特的参数化, 场景被划分为多个元素,这些元素被压平并打包成一个共同的纹理。 例如,左下角的剖面对应于地面,显示了立方体的两个阴影。
必须小心确保图表不仅不重叠,而且它们的过滤足迹(filtering footprints)必须保持分离。当渲染一个给定的图表时,所有可以访问的像素(双线性滤波访问四个相邻的像素)都应该被标记为使用过的,这样就不会有其他图表与它们重叠,否则,图表之间可能会出现bleeding现象,其中一个图表的光照可能会在另一个图表上可见。尽管为光照贴图系统提供一个用户控制的“gutter”量用于灯光地图图表之间的间距是相当普遍的,但这种分离是不必要的。使用一组特殊的规则,可以在光照贴图空间中对图表进行栅格化,从而自动确定图表的正确过滤足迹。
看上图:为了准确地确定一个图表的过滤足迹,我们需要找到渲染期间可以访问的所有纹素。 如果一个图表与四个相邻像素中心之间的正方形相交,那么所有这些像素都将用于双线性滤波。 纹素网格用实线标记,纹素中心用蓝点,图表用粗实线进行栅格化(左)。 我们首先将图表栅格化为移动了半像素大小的网格,并以虚线(中间)标记。 任何接触标记单元格的纹素都被认为占用(右)。
Greger等人提出了irradiance volume,通过irradiance环境贴图的稀疏空间采样表示五维(三个空间和两个方向)irradiance函数。 也就是说,在空间中有一个三维网格,在每个网格点上都有一个irradiance环境贴图。 动态对象从最近的贴图中插值irradiance值。 Greger等人使用两级自适应网格进行空间采样,但也可以使用其他体积数据结构,如八叉树。
存储的样本点irradiance函数的最常见表示包括:
- 球谐(SH)的二阶和三阶,前者更常见,因为一个颜色通道所需的四个系数方便地打包到四个纹理的通道。
- 球形的高斯函数(Spherical Gaussians)。
- 环境立方体或环境六面体(dice)。
irradiance volume也可以为静态表面提供光照, 这样做的好处是不必为光照贴图提供单独的参数化, 这种技术也不会产生裂缝。 静态和动态物体都可以使用相同的表示,使两种几何类型之间的光照一致。 在延迟着色(第20.1节)中,体积表示很方便使用,其中所有光照都可以在一次pass中执行, 其主要缺点是内存消耗比较大。 光照贴图所使用的内存大小与分辨率的平方成正比; 对于一个规则的体积结构,它与立方体一起增长。 由于这个原因,网格体积表示使用了相当低的分辨率。 自适应、分层形式的光照Volumes具有更好的特性,但它们仍然比光照贴图存储更多的数据, 它们也比有规则间隔的网格慢,因为额外的在着色器代码中创建加载依赖,这可能导致更慢的执行。
Unity引擎使用一个四面体网格来插值一组光照探针。
从一个四面体网格中采样的光照质量高度依赖于网格的结构,而不仅仅是probes的总体密度。 如果它们不均匀分布,产生的网格可能包含产生视觉artifacts的细长四面体。 如果用手放置probes,问题可以很容易地纠正,但这仍然是一个手动过程。 四面体的结构与场景的几何结构没有关系,所以如果处理不当,灯光将会在墙壁上插入并产生bleading artifacts,就像irradiance volume一样。 在手动放置probes的情况下,可以要求用户插入额外的probes以防止这种情况发生。 当使用自动放置probes时,可以在probes或四面体上添加某种形式的可见性信息,以将其影响限制在相关区域。
对静态和动态物体使用不同的光照存储方法是一种常见的做法。 例如,静态网格可以使用光照贴图,而动态对象可以从体积结构中获得光照信息。 虽然很受欢迎,但这种方案可以在不同类型的几何形状之间创建不一致的外观。 其中的一些差异可以通过regularization来消除,在regularization中,光照信息在表示中被平均。
动态漫反射全局光照:
尽管预计算光照可以产生非常好的效果,但它的主要优点也是它的主要缺点——它需要预计算, 这种离线流程可能会很长。 在典型的游戏关卡中,光照baking需要花费数小时的时间。 因为光照计算需要很长时间,美工通常被迫同时处理多个关卡,以避免等待baked完成时的停工时间。 这反过来又会导致用于渲染的资源负载过大,并导致bakiing时间更长。 这种循环会严重影响生产力并导致挫败感。 在某些情况下,甚至不可能预先计算光照,因为几何图形在运行时发生变化或在某种程度上由用户创建。
Tabellion和Lamorlette表明,在许多情况下,一次bounces就足以产生令人信服的结果。 这是一种离线方法,但它启发了Dachsbacher和Stamminger的一种方法,即反射阴影贴图(RSM)。
类似于常规阴影贴图,反射阴影贴图是从光线的角度渲染的。 除了深度之外,它们还存储了其他有关可见表面的信息,如反照率、法线和直接光照(通量)。 当执行最后的着色时,RSM的像素被当作点光源来提供间接照明的单一bounce。 因为一个典型的RSM包含成百上千个像素,所以使用重要性驱动的启发式只选择其中的一个子集。 Dachsbacher和Stamminger后来展示了如何通过反射过程来优化该方法, 即不是从RSM中为每个着色点选择相关的像素,而是基于整个RSM和屏幕空间中的splatted创建一些灯。
该方法的主要缺点是它不能为间接照明提供遮挡, 虽然这是一个近似,但结果看起来是可信的,并且在许多应用程序中是可接受的。
为了达到高质量的效果,并在光传输时保持时间稳定,需要创建大量的间接光。 如果创建的太少,它们往往会在RSM重新生成时迅速改变它们的位置,并导致闪烁现象。 另一方面,从性能的角度来看,过多的间接光源是一个挑战。 Xu描述了该方法是如何在《神秘海域4》中执行的。 为了保持在性能限制范围内,他在每个像素上使用少量的光,但是在几个帧上循环使用不同的光集,并暂时过滤结果,如图:
人们提出了不同的方法来解决间接遮挡的不足。 Laine等人使用双抛物面阴影贴图作为间接光源,但将它们增量地添加到场景中,因此在任何一帧中只有少量的阴影贴图被渲染。 Ritschel等人使用简化的、基于点的场景表示来渲染大量不完美的阴影贴图。 当直接使用时,这样的贴图很小,包含很多缺陷,但经过简单的过滤后,提供了足够的保真度,为间接照明提供适当的遮挡效果。
RSM:
这里讲一下RSM。
基本思想:
在第一个Pass,RSM算法需要记录哪些场景面元被直接光照照亮,将这些被直接光照照亮的面元几何信息和着色信息存储记录下来;所以第一个pass会从光源视角渲染整个场景
在第二个Pass,根据前面得到的直接光照照亮面元的信息,计算这些面元对其他场景物体的光照。
这里计算其实是rsm比较难想的一个地方,后面会专门出一期讲各种全局光照算法的文章,到时候再细讲。
LPV:
基本步骤:
- (1)直接光照的信息生成;
- (2)将直接光照得到的虚拟光源注入到三维体素网格中;
- (3)体素网格之间的辐射率扩散、传播;
- (4)根据传播得到的辐射率进行间接光照的计算。
步骤1简述:
在步骤(1)中,LPV算法从光源的角度渲染整个场景,然后将深度信息、顶点位置、法线向量和反射通量保存到贴图纹理当中。
步骤2简述:
在步骤(2)时,创建一个三维的体素网格(3D纹理),然后根据贴图的信息,将有几何体的贴图像素当作一个虚拟光源,根据贴图上存储的顶点位置找到其对应的体素格子,将反射通量注入保存到这个体素格子中,从而完成虚拟光源注入的过程。
每个体素网格的中心可以看成是一个点光源。但值得注意的是,格子中心的点光源并不是向所有方向均匀辐射的!因为在注入阶段,格子中心仅仅在某些方向被注入了虚拟光源。因此,为了描述格子中心向不同方向的辐射情况,LPV采用了球面谐波函数来描述其球面方向上的辐射率分布情况。
LPV论文的作者采用了前两阶(也就是前四个)球面谐波函数来存储格子中心的辐射率分布。
步骤3简述:
步骤(3)的体素格子之间的辐射率传播采用迭代扩散的方式进行。在每一次迭代过程中,每个体素格子向与其直接相邻的格子传播辐射率(下图所示,三维情况是6个相邻格子)。依次迭代下去,直到一定的迭代次数,论文实践表明4次的迭代能够取得不错的效果。
步骤4简述:
最后的步骤(4)其实不言自明。在计算过程的时候,找到着色点对应的体素格子,从中取出球面谐波的权重系数,还原出给定方向上的辐射率,完成间接计算的过程。
基于体素的方法:
VXGI:
场景体素化:
基于GPU的三维体素化大致思想就是:首先计算出需要体素化模型的AABB包围盒,然后将模型投影到AABB包围盒的某个平面上,经过渲染管线的光栅化插值操作,我们可以在片元着色器得到每个像素点对应的世界空间的顶点坐标,根据这个顶点坐标标记三维空间数组(这个三维空间数组就是根据体素划分的空间序列)的相应位置,最后在CPU端读出这个三维空间数组,若当前的数组位置有标记,则将该数组位置对应的立方体作为一个体素。可以看到,整个流程思路非常清晰,但是还需要借助一些手段修正算法存在的缺陷,修补方法这里就不多讲了。
直接光照pass:
生成了3D体素纹理之后,紧接着的步骤是直接光照的Pass。直接光照Pass可以直接借用RSM机制来实现,即从光的视角来渲染整个场景,将直接光照的数据存储到贴图中,然后再将贴图里面的直接光照数据注入到场景体素化的3D纹理当中。然后再为这些3D纹理生成Mipmap,如下图所示(Clipmap本质上就是在Mipmap的基础上加了个裁剪范围,使得显存只需要加载每个Mipmap层次的一部分,这里不细说)
间接光照pass:
间接光照Pass是从摄像机的角度渲染整个场景,并根据上面的Mipmap结构对场景发射射线进行追踪来计算间接光照部分。这里发射追踪的射线是具有一定角度的圆锥体。但圆锥体也并不是真正意义上的圆锥体,而是由不同level的体素拼接而成的类锥体的形状,如下图所示,从近到远,体素的大小逐渐增大。
VXGI可以实现非常惊艳的全局光照效果,但是它的缺点也显而易见:3D纹理太过耗费显存,体素化的精度决定了光照精度,而且也存在一些漏光的artifact现象。
屏幕空间方法:
漫反射的屏幕空间方法主要有ssao,ssdo,基于raymarching的ssgi吧
ssao和ssdo的区别主要是ssdo对于每一个采样点p,对比该采样点的深度与该采样点对应到的深度贴图上的深度,如果采样点被遮挡了(深度值大于贴图上的深度值),那么就计算遮挡位置的直接光照信息作为p点的间接光照(例如A点对应的橙色点),而ssao这一部分仅仅计算遮挡值。
SSDO当然也不是物理准确的,上图的最右边图片所示,A点对应的z1点并不会对p点产生间接弹射的贡献,但是他缺取用了。并且,采样的半球半径限制了弹射范围,只有在半球半径范围内的点才会被考虑进来,因此不会渲染超过一定范围内的间接弹射效果。最后需要注意的就是,SSDO是基于屏幕空间的,因此它所有的间接光照信息都来源于当前摄像机能够看到的,对于那些看不到的面元,自然也就不会贡献间接光照的效果。
高光全局光照:
IBL:
这里只讲述ibl的镜面ibl反射项
split sum approximation:
我们将反射方程分割成这样
预滤波环境贴图:
split sum之后的方程左边称为预滤波环境贴图。它类似于辐照度图,是预先计算的环境卷积贴图,但这次考虑了粗糙度。因为随着粗糙度的增加,参与环境贴图卷积的采样向量会更分散,导致反射更模糊,所以对于卷积的每个粗糙度级别,我们将按顺序把模糊后的结果存储在预滤波贴图的 mipmap 中。例如,预过滤的环境贴图在其 5 个 mipmap 级别中存储 5 个不同粗糙度值的预卷积结果,如下图所示:
表面越粗糙则反射得越模糊得现象其实涉及到一个反射波瓣的问题,所以的反射波瓣就是反射光线的分布范围。如下图5所示,对于一个光滑的完美镜面,其反射波瓣就是反射向量,越粗糙则反射波瓣越大,且基本上都是以反射向量为中心。
所以我们需要做重要性采样。 为了加速蒙特卡洛积分方法的收敛速度,Epic Games公司提出使用超均匀分布序列(Low-discrepancy Sequence)——Hammersley序列。相对于普通的伪随机数,Hammersley序列的随机数分布更加均匀,如下图6所示,将其应用到蒙特卡洛采样能够提升收敛速度。
然后我们需要将这个二维的序列转换成我们对半球方向的三维采样,同样我们利用球面坐标和笛卡尔坐标之间的关系,首先将Hammersley序列xi=(u,v)T∈HN映射到(ϕ,θ),然后转换成笛卡尔坐标下的向量形式。一个均匀映射和一个余弦映射公式如下:
我们将结合之前PBR提到的法线分布函数,法线分布函数给定一个法线向量,它返回微平面法线与给定法线朝向一致的分布概率。Trowbridge-Reitz GGX法线分布函数的数学定义为:
我们将法线分布函数与余弦映射结合起来做重要性采样:
然后根据上面的知识我们就能够计算预滤波环境贴图,后面就不多讲了。
预计算BRDF:
这部分实际上就比较简单,我们把各种情况的BRDF存到一张纹理上,这个纹理通常被称作lut。这张纹理的u坐标为粗糙度,v为cos(n*l),我们输入这两个值就能够获得对应的brdf结果。
但是原始的brdf函数积分基于三个变量,cos(n*1),粗糙度,F0(菲涅尔方程输入的基础值),我们需要简化一下这个方程:
将Fresnel-Schlick 近似公式替换右边的F,可以得到:
在简单拆分一下:
这样我们就能够构建基于n⋅ωo和粗糙度roughness的二维查找表了,在实现中,我们通常渲染屏幕空间大小的四边形,遍历n⋅ωo和粗糙度的所有取值,计算上述公式的两项积分的结果,存储为纹理的像素值vec2(左边积分结果,右边积分结果)。
基于预滤波环境贴图和预计算的BRDF,我们很容易得到IBL的高光反射项了。
基于体素的方法:
我们考虑VXGI的高光反射项,在VXGI的慢反射项中我们需要对各个方向都做体素追踪,但是对于高光反射项我们只需要对反射方向做体素追踪,然后在这个方向上做光照计算就可以。
平面反射:
平面反射最主要的是做在平面的对称另一侧做一个虚拟相机,然后渲染一次场景,把结果作为一张render texture,然后我们可以把这张render texture作为全局光照的高光反射项,通过矩阵变换来求出着色点需要采样的位置。做这个方法需要做一个合适的裁剪面,因为在反射面的远侧(即后面)的物体不应该被反射,这个平面的近平面应该与平面重合。
屏幕空间的方法:
SSR:
基本思想:
ssr的基本思想比较简单,根据gbuffer里面存储的数据,取每个fragment然后计算出reflect方向,然后以这个fragment位置和reflect做ray的origin和dir,做raymarching,如果打到物体则做光照计算作为间接光照。
着重讲一下raymarching部分,每一次光线步进,我们都会做一次相交判断。相交判断的逻辑为:将当前的步进点pp的深度值与pp点对应的深度贴图上的深度值进行大小判断,如果pp点的深度值大于深度图贴图上的深度值,那么就说明当前步进的点落到某个场景表面之下,这时就发生了相交。最为Naive的光线步进就是Linear Ray-marching,也就是每次步进一小段固定的距离。
问题:
光线步进是在三维世界空间做的,所以每一次都要把步进的点投影到屏幕上。但是在三维空间做固定长度的光线步进,投影到屏幕上步进的间隔并非均匀的。这就会出现两个问题,遗漏采样和重复采样。看下面这个图:
左图越红代表重复采样的次数越多,右图表示均匀采样。
解决方法:
可以把处理全部都转化到屏幕空间中,即对于线段起始点 Q0 和结束点 Q1 ( Q0,Q1 是世界空间的点),首先将其转换到屏幕空间中得到点 H0,H1 (屏幕空间中的点是二维点只有 x,y 分量)。如此一来对于点 Q0,Q1 就可以借助DDA画线算法的思想来进行采样(原本的画点操作就变成了采样操作)。这样的好处就在于绝不会重复采样,也保证会连续采样。
注意:由于在屏幕空间进行Ray Marching丢了 Z 值信息,无法进行深度比较,因此还需要单独保存当在屏幕空间从 H0 变化到 H1 的 Z 值。
学习资料:
核心:《Real-Time Rendering》 Chapter 11 Global Illumination
1.理论 - LearnOpenGL CN
2.【《Real-Time Rendering 3rd》 提炼总结】(八) 第九章 · 全局光照:光线追踪、路径追踪与GI技术进化编年史 - 知乎
3.蒙特卡洛积分 - 知乎
4.从NDC(归一化的设备坐标)坐标转换到世界坐标的数学原理 - 爱码网
5.法线贴图 - LearnOpenGL CN
6.11.5 漫反射全局光照 - 知乎
7.高质量实时渲染:实时环境光 | YangWC's Blog
8.Global Illumination_Screen-Space Ray Tracing(SSR)_沉默的舞台剧的博客-CSDN博客
![实时高清渲染:全局光照(Global Illumination)[2]---漫反射/高光全局光照_第1张图片](http://img.e-com-net.com/image/info8/acb4e9434d0b4248ac6db41a754a063e.jpg)
![实时高清渲染:全局光照(Global Illumination)[2]---漫反射/高光全局光照_第2张图片](http://img.e-com-net.com/image/info8/54d0ff823b474e4895a6907743808d44.jpg)

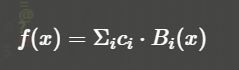



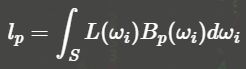


![实时高清渲染:全局光照(Global Illumination)[2]---漫反射/高光全局光照_第3张图片](http://img.e-com-net.com/image/info8/5c4ba81401a44d408e80cad42d05eb97.jpg)
![实时高清渲染:全局光照(Global Illumination)[2]---漫反射/高光全局光照_第4张图片](http://img.e-com-net.com/image/info8/e472e9ee8eed49ba9e9a5152ab3be896.jpg)
![实时高清渲染:全局光照(Global Illumination)[2]---漫反射/高光全局光照_第5张图片](http://img.e-com-net.com/image/info8/c6163f5e3d0b4ffe87bb33387852d28f.jpg)
![实时高清渲染:全局光照(Global Illumination)[2]---漫反射/高光全局光照_第6张图片](http://img.e-com-net.com/image/info8/2a8d6d1278f449d4a09c0c700b1e10fc.jpg)
![实时高清渲染:全局光照(Global Illumination)[2]---漫反射/高光全局光照_第7张图片](http://img.e-com-net.com/image/info8/23e8d54e8b964b3d946294afee6d9afb.jpg)
![实时高清渲染:全局光照(Global Illumination)[2]---漫反射/高光全局光照_第8张图片](http://img.e-com-net.com/image/info8/14157dc2b2874fa7ac88d6b26115f880.jpg)
![实时高清渲染:全局光照(Global Illumination)[2]---漫反射/高光全局光照_第9张图片](http://img.e-com-net.com/image/info8/8dc2ae6f22754354a11b2681b3f70d2c.jpg)
![实时高清渲染:全局光照(Global Illumination)[2]---漫反射/高光全局光照_第10张图片](http://img.e-com-net.com/image/info8/23b4f87f2af44b60ac4632a7264e488d.jpg)
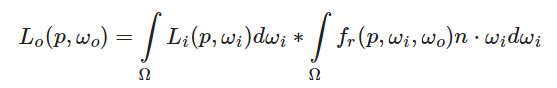
![实时高清渲染:全局光照(Global Illumination)[2]---漫反射/高光全局光照_第11张图片](http://img.e-com-net.com/image/info8/39aee4d6a7544e689aad88c89dd82f9d.jpg)
![实时高清渲染:全局光照(Global Illumination)[2]---漫反射/高光全局光照_第12张图片](http://img.e-com-net.com/image/info8/e7746aae2f5945e9b5724a3298619095.jpg)
![实时高清渲染:全局光照(Global Illumination)[2]---漫反射/高光全局光照_第13张图片](http://img.e-com-net.com/image/info8/6802356d190d4385bdc939eae209ae2b.jpg)
![实时高清渲染:全局光照(Global Illumination)[2]---漫反射/高光全局光照_第14张图片](http://img.e-com-net.com/image/info8/cbc0ee6f7edd4cbc80a27361a0374b76.jpg)

![实时高清渲染:全局光照(Global Illumination)[2]---漫反射/高光全局光照_第15张图片](http://img.e-com-net.com/image/info8/9ca16aee206c4f75ab7ee8b01db3900a.jpg)
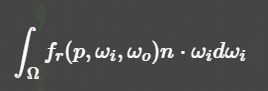
![实时高清渲染:全局光照(Global Illumination)[2]---漫反射/高光全局光照_第16张图片](http://img.e-com-net.com/image/info8/5376f6b856c04e058c5a268a92d3b07e.jpg)
![实时高清渲染:全局光照(Global Illumination)[2]---漫反射/高光全局光照_第17张图片](http://img.e-com-net.com/image/info8/cced1c6a13054b62a135b7660d373bd7.jpg)
![实时高清渲染:全局光照(Global Illumination)[2]---漫反射/高光全局光照_第18张图片](http://img.e-com-net.com/image/info8/43f20d0820bd417485f615b3351e9948.jpg)
![实时高清渲染:全局光照(Global Illumination)[2]---漫反射/高光全局光照_第19张图片](http://img.e-com-net.com/image/info8/4c473f2f64104107b8e1a0143127fcd9.jpg)
![实时高清渲染:全局光照(Global Illumination)[2]---漫反射/高光全局光照_第20张图片](http://img.e-com-net.com/image/info8/3f38dbf8632945749f5aa8ea349ba5c9.jpg)