计算机视觉之正负样本不均衡问题

Anchor-based的目标检测器通过Anchor来得到一系列密集的候选框，然后按照一定阈值将候选框分成真样本（前景）和负样本（背景），最后按照一定的采样策略来进行训练。目标检测中广泛采用的采样策略是随机采样（正样本和负样本按照一定比例随机采样），然而随机采样并不能保证能够选取得到更有价值的样本（使检测器更鲁棒）。
在探索更有效的采样策略的过程中，产生了两类方法：
Hard Sampling：从所有候选样本中选择子集来训练模型。（包含hard negative mining、OHEM、IoU-balanced Sampling等等）
Soft Sampling：为所有候选样本安排不同的权重值。包括（Focal Loss、GHM、PISA等）
1、Focal Loss

在Focal Loss for Dense Object Detection 文章中提出的RetinaNet是最近很流行的Anchor-free检测器的标配，Focal loss的提出引起了Soft Sampling研究的热潮，后面对Focal loss的分析写的很出彩。
Motivation
作者提出前景和背景类别的极度不平衡是造成单阶段检测器精度差的主要原因。
类别不平衡会产生两个问题：
①、大量容易负样本(不提供有用的学习信息)会导致训练过程无效。
②、大量容易负样本产生的loss会压倒少量正样本的loss（即容易负样本的梯度占主导），导致模型性能衰退。

Cross Entropy

首先定义二分类的cross entropy(CE)loss为：

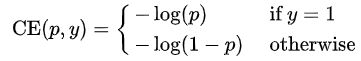
上式的y∈{±1}特指gt的类别，p∈[0,1]是模型估计的标签为y=1的概率。为了方便起见，定义pt为：

并且重写cross entropy（CE）loss为CE（p，y）=CE（pt）=-log（pt）
预测值和标签相近，loss就低，预测值和标签远离，loss就高。
Balanced Cross Entropy
处理类别不平衡的一般方法为引入权重因子α∈[0,1]，类别为1的权重值为α，类别为-1的权重值为1-α。为了方便起见，如定义pt一样的方式定义αt，α-balanced CE loss为：

Focal Loss Definition

虽然α能够平衡正样本和负样本的重要性，但是不能平衡容易样本和困难样本的重要性。因此，作者修改了loss函数来降低容易样本的权重值，使得训练过程更加关注hard negative example（即预测值背离标签的样本）。
形式上，在cross entropy loss前面添加一个调制因子(1-pt)的γ次方，且γ≥0，定义focal loss为：
focal loss有两个性质：
①、当样本错误分类时，pt偏小，调制因子接近于1并且loss不受影响的。当pt->1时，调制因子趋向于0，对于容易分类样本来说，等同于loss的权重值降低。
②、聚焦参数γ平滑地调整容易样本降低权重值的速率。当γ=0时，FL等同于CE，随着γ的增加，调制因子的影响会同步的增加。
实际使用中，使用的是α-balanced辩题的focal Loss：

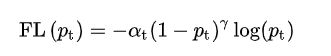
focal loss在实际使用中还有两个重要的小细节：
①一张图片中的focal loss是对~100k的Anchor求focalloss的和得到的，然后通过一个gt box的Anchor数量进行归一化。因为大量的Anchors是容易负样本，在focal loss下得到loss值非常小，如果用所有Anchors的数量进行归一化，会导致归一化后的loss值非常小。
②当只使用α时，将α偏向于样本少的类别，当同事使用α和γ时，α和γ需要向相反的方向变化（实验中最佳的参数设置为α= 0.25和γ=2）

Analysis of the Focal Loss

为了更好的理解focal loss，作者仔细分析了loss的经验分布。采用默认的ResNet101,600输入，γ=2的模型。作者将这个模型使用到大量的随机图片上，并且采样得到_{10的7次方个负样本和}10的5次方个正样本的预测概率。然后，将正负样本分开，计算出这些样本的FL并且归一化loss使得和为1。得到归一化的loss后，就能够从小到大排序loss并且绘制出cumulative distribution function (CDF)。

正样本在不同 γ下的CDF基本相同。举个例子，大约有20%的最难正样本占据了大约一半的正样本loss，随着γ的增加，更多的loss集中在20%的最难正样本上，但是影响很小。
而负样本在不同γ下的CDF表现完全不同。当γ=0时。正样本和负样本的CDFs非常相似。然而，随着γ的增加,更多的loss集中在20%的最难正样本上，但是影响很小。
从以上分析可以看出，FL可以有效的降低容易样本的影响，将所有的注意力集中在苦难样本上。

focal loss具体形式并不是关键。作者提出了另外一种focal loss的形式能够取得可比较的结果。

作者首先考虑与上文有所不同的CE和FL的形式。定义数值 xt如下：
xt=yx
y∈{±1}特指gt类别。定义
（pt与之前的定义的pt是一致的）。当xt>0时，样本被正确的分类，这种情况下pt>.5
使用xt就能够定义一个focal loss的替换形式。
FL有两个参数γ和β，能够用来控制loss曲线的陡度（steepness）和位移（shift）和FL一样，FL能够降低容易样本的权值。采用和上述FL一样的设置，模型能够实现相当的精度。

蓝色线表示AP大于33.5的有效设置。如图所示，容易样本（xt>0）的loss下降。更一般的，任何和FL，FL有相似性质的函数同样有效。

CE，FL和FL的导数为：

所有loss函数，随着预测置信度的增加梯度趋向于-1或者0.然而，当xt>0时，FL和FL*梯度非常小。

2、GHM

由Focal Loss附录的图可以看出，当梯度绝对值越大时，loss值也越大（即梯度和苦难样本存在某种关系），这一点可能启发了GHM的工作。为了降低复杂度，使用了unint region approximation。

Motivation

目标检测器中存在着两个问题：正负样本的不平衡和难易样本的不平衡。
Focal Loss虽然部分解决了这两个问题，但是Focal Loss采用了2个超参数，需要大量实验进行调参。

如果从整体来看，大量负样本通常是容易样本，大量正样本是苦难样本，因此，两种不平衡可以粗略的归结为属性不平衡（或者说类别不平衡）。

作者指出类别的不平衡可以归结为难度的不平衡，难度的不平衡可以归结为梯度范数分布的不平衡。

可以通过梯度范数分布来表示不同属性的不平衡，为了方便起见， 将关于梯度范数的样本密度称为梯度密度。梯度范数非常小的样本占据着相当大的密度。虽然容易样本对于全局梯度的贡献少于困难样本，但是大量容易样本总的贡献压倒了少量困难样本总的贡献，另外，作者还发现梯度范数非常大的样本密度大于介于中间的样本的密度。作者认为这些非常困难的样本可以当做异常呀昂本，因为当模型稳定时，这些异常样本仍然存在。这些异常样本可能影响模型的稳定性，因为异常样本的梯度可能和其他样本的梯度有巨大差异，如果收敛模型被迫去学习如何地对这些异常样本进行分类，那么会导致其他样本分类精度的衰退。

通过上述分析，作者提出一个梯度协调机制（ gradient harmonizing mechanicam 简写为GHM）来有效训练检测器，该梯度协调机制可以在训练过程中调整不同样本的梯度贡献。GHM首先对梯度密度相似的样本的数量进行统计，然后根据梯度密度在每个样本的梯度上附加一个协调参数。利用GHM进行训练时，容易样本产生大量累积梯度可以很大程度上降低权值，另外异常值也可以相对降低权值，最终导致每种样本的贡献会趋于平衡，训练过程会更加有效和稳定。

实际中，梯度的修改可以通过重新设计损失函数来等效的实现，我们将GHM嵌入到分类损失中，该分类损失被称为GHM-C loss，这种损失函数不需要超参数进行调整。由于梯度密度是一个统计变量，取决于小批量的样本分布，所以GHM-C是一种动态loss，可以适应每个批次的数据分布变化以及模型的更新。
为了显示出GHM的通用性，在回归分支中利用它来构成GHM-R loss。

首先定义二分类的cross entropy（CE）loss 为：

其中p∈[0,1]是模型预测出来的概率，而p*∈{0,1}为gt的类标签
设x为模型的直接输出，于是可将p定义为票= sigmoid（x），对x求梯度：

g的定义如下：

g等于x的梯度范数，g值表示样本的属性并且隐含着样本对全局梯度的影响。

Gradient Density

梯度密度函数的定义如下：

其中gk是第k个样本的梯度范数，那么δ∈（x，y）和l∈（g）定义为：

g 的梯度密度是以 g 为中心∈ 为宽范围内的样本数量通过有效范围的宽度进行归一化得到的。

接着定义梯度密度协调参数为：
N是样本总数。为了更好的理解梯度密度协调参数，可以将βi改写成

分母
是对梯度位于 gi范围的部分样本进行归一化。如果所有样本的梯度是统一分布的，那么对于任意gi 都有GD（gi）=N ，并且每个样本都有相同的βi=1 ，这意味着没有任何改变。如果样本具有大的梯度密度，那么归一化后会导致权值下降。
通过将 βi作为loss的权值嵌入到分类loss中，梯度密度协调的分类loss定义如下：
从图中可以看到，Focal Loss和GHM-C有相似的趋势，这说明超参数最优的Focal Loss与梯度均匀协调的GHM曲线相似。另外，GHM-C比起Focal Loss多了一个优点：降低异常样本的权值。

GHM-R Loss

3.PISA

PISA跳出了Focal Loss的思路，认为应当从mAP这个指标出发，来设计采样策略。

Motivation

虽然随机采样和hard sampling简单且广泛采用，但不一定是训练有效探测器的最佳采样策略。一个开放的问题是：用来训练目标探测器的最重要的样本是什么？

作者揭示了设计采样策略时需要考虑两个重要方向：

①.样本不应该被认为是独立的和同等重要的。基于区域的目标检测是从大量候选框中选取一小部分边界框，以覆盖图像中的所有目标。因此，不同样本的选择是相互竞争的，而不是独立的。一般来说，检测器更可取的做法是在确保所有感兴趣的目标都被充分覆盖时，在每个目标周围的边界框产生高分，而不是对所有正样本产生高分。作者研究表明关注那些与gt目标有最高IOU的样本是实现这一目标的有效方法。

②目标的分类和定位是有联系的。准确定位目标周围的样本非常重要，这一观察具有深刻的意义，即目标的分类和定位密切相关。具体地，定位好的样本需要具有高置信度好的分类。
受上述研究的启发，作者提出了Prime Sample Attention(PISA)，这是一种简单而有效的方法，用于对区域进行采样和学习目标检测器，作者将那些起着更重要作用的样本作为主要样本。 具体而言，定义IoU分层局部排序(IoU Hierarchical Local Rank简写为IoU-HLR)来对每个小批量中的样本进行排序。 该排序策略将每个目标周围的最高IoU的样本放置在排序列表的顶部，并通过简单的权值重标定方案将训练过程的重点引导到排序列表的顶部。 作者还设计了分类感知的回归损失来共同优化分类和回归分支。 具体地，这个loss将抑制掉那些回归loss大的样本，从而加强了对主要样本的注意。
Prime Samples

引入Prime Samples的概念，指那些对目标检测性能有重大影响的样本。具体地，作者通过回顾mAP指标来研究不同样本的重要性，研究显示每个样本的重要性取决于它和gt的IoU。因此，作者提出一种新颖的IoU-HLR排序策略，作为一种评估重要性的定量方式。

A Revisit to mAP

给定一个带标注gt的图片，当边界框满足以下两个条件时，标记为正样本。

1.边界框和最近的gt的IoU大于阈值 Θ 时

2.如果gt没有IoU大于阈值的边界框，则选择IoU最大的边界框

剩余没有标记的边界框作为负样本。

mAP指标揭露了对于目标检测器来说更重要样本的2个准则：

1.在所有和gt目标重合的边界框中，IoU最高的边界框时最重要的，因为它的IoU值直接影响召回率。

2.所有不同目标的最高IoU边界框中,具有更高的IoU的边界框更加重要,因为它是随着 θ 增加最后一个低于阈值 θ 的边界框,从而对整体精度有很大的影响。

IoU Hierarchical Local Rank (IoU-HLR)
基于上述分析，作者提出了IoU-HLR来对小批量边界框样本的重要性进行排序。这个排序是以层次的方式计算的，它既反映了局部的IoU关系(每个ground truth目标周围)，也反映了全局的IoU关系(覆盖整个图像或小批图像)。值得注意的是，不同于回归前的边界框坐标，IoU-HLR是根据样本的最终定位位置来计算的，因为mAP是根据回归后的样本位置来计算的。

我们首先将所有的样本根据它们最近的gt目标分成不同的组。接下来，我们根据每个组的IoU和gt按降序排列样本，得到IoU-LR。随后，我们使用相同的IoU-LR采样，并按降序排序。具体来说，所有top1的IoU-LR样本都被收集和排序，然后是top2、top3等等。这两个排序阶段导致了一个批次的所有样本之间的线性顺序，即IoU-HLR。

IoU-HLR遵循上述两个准则。首先，它将那些局部排序较高的样本放在前面，这些样本对于每一个单独的gt目标来说是最重要的。其次，在每个局部组内，根据IoU对样本进行重新排序，这符合第二个准则。值得注意的是，那些排在列表前面的样本，通常能够确保高精度，因为它们直接影响召回率和精确度，尤其是当IoU阈值较高时;在实现高检测性能时，列表后面的样本就不重要了。
在相同的情况下(如总损失减少10%)，增加IoU-HLR下top5和top25的样本的得分，并分别用虚线和点线绘制PR曲线。结果表明，只关注最重要的样本比平等关注更多的样本要好。
图中绘制出了random、hard、prime samples的分布。可以观察到，prime samples往往同时有高IoU和低分类loss，而hard samples往往有更高的分类loss并沿IoU轴分布范围更广。表明这两个采样策略具有本质上不同的特性。

Learn Detectors via Prime Sample Attention

作者提出Prime Sample Attention，一种简单且有效的采样策略，该采样策略将更多的注意力集中到主要样本上。PISA由两个组件组成：基于重要性的样本权值重标定(Importance- based Sample Reweighting简写为ISR)和分类感知的回归损失(Classification Aware Regression Loss简写为CARL)。PISA在训练过程中更关注主要样本，而不是平等对待所有样本。首先，主要样本的loss权值大于其他样本，因此分类器倾向于对这些样本预测更高的分数。其次，构造一个联合目标对分类和回归进行学习，从而提高主要样本的分数。

Importance-based Sample Reweighting
IoU-HLR作为重要性的衡量指标，首先将排序转化为线性映射的真实值。根据线性映射的定义，IoU-HLR在每个类中分别进行计算。对于类 [公式] ，假设总共有 nj个样本，通过IoU-HLR表示为
，其中
，然后使用一个线性函数转换 ri为 ui ， ui 表示为类j的第i个样本的重要程度
采用指数的形式来进一步将样本重要性 ui转换为loss权值 wi 。 γ 表明对重要样本给予多大的优先权的程度因子，β 是决定最小样本权值的偏差。

通过提出的权值重标定策略，可以将交叉熵重写成：
n和 m是正样本和所有样本的总数， si和si^ 表示第i个样本的预测分数和分类目标。值得注意的是，简单的添加loss权值将会改变总的loss值并且改变正样本和负样本的比例，因此，为了保持正样本总的loss值不改变，作者将 wi 归一化为 wi’
Classification-Aware Regression Loss

受到分类和定位是相关的，由此受到启发，作者提出了另一种方法来关注主要样本。作者提出使用分类感知的回归损失(CARL)来联合优化分类和回归两个分支。CARL可以提升主要样本的分数，同时抑制其他样本的分数。回归质量决定了样本的重要性，我们期望分类器对重要样本输出更高的分数。两个分支的优化应该是相互关联的，而不是相互独立的。

作者的解决方法是让回归损失能够感知到分类分数，这样梯度就可以从回归分支传递到分类分支。公式如下：
pi表示相应类别的预测分数，di表示输出的回归偏移量。利用一个指数函数将 pi转化为vi ，随后根据所有样本的平均值对它进行缩放。为了保持损失规模不变，对具有分类感知的 ci 进行归一化。 L 是常用的smooth L1 loss。

Lreg 关于ci’ 的梯度与原回归损失L(di,di^) 成正比。 Lreg关于pi 的梯度与L(di,di^{)正相关。即回归损失越大的样本分类得分的梯度越大，说明对分类得分的抑制作用越强。从另一个角度看，L(di,di}) 反映了样本i的定位质量，因此可以认为是一个IoU的估计，进一步可以看作是一个IoU-HLR的估计。可以近似认为，排序靠前的样本有较低的回归损失，于是分类得分的梯度较小。对于CARL来说，分类分支受到回归损失的监督。 不重要样本的得分被极大的抑制掉，而对重要样本的关注得到加强。

总结
Focal Loss认为正负样本的不平衡，本质上是因为难易样本的不平衡，于是通过修改交叉熵，使得训练过程更加关注那些困难样本，而GHM在Focal Loss的基础上继续研究，发现难易样本的不平衡本质上是因为梯度范数分布的不平衡，和Focal Loss的最大区别是GHM认为最困难的那些样本应当认为是异常样本，让检测器强行去拟合异常样本对训练过程是没有帮助的。PISA则是跳出了Focal Loss的思路，认为采样策略应当从mAP这个指标出发，通过IoU Hierarchical Local Rank (IoU-HLR)，对样本进行排序并权值重标定，从而使得recall和precision都能够提升。

我认为PISA的方法有一个问题，就是只考虑了IoU的排序，但是没有考虑到即使是相同IoU的样本的重要程度也是不相同的，比如有两个相同IoU的样本，一个位于目标的内部(如下图1)，另一个没有在目标的内部(如下图2)，显然第一个样本应当比第二个样本重要，如果后面要对PISA方法进行改进的话，可能需要引入一个有效主要样本的概念。
参考：https://zhuanlan.zhihu.com/p/63954517