Python--时间序列一本通----实例大舞台，有码你就来
开局附后面例子的数据源：https://github.com/keefecn/python_practice_of_data_analysis_and_mining/blob/master/chapter5/demo/data/arima_data.xls
概述
常用按时间序列排序的一组随机变量X1,X2,…,Xt（例如1月2月…）来表示一个随机事件的时间序列，简记为{Xt}；用x1,x2,…,xt或{xt，t=1,2,…n}来表示该随机序列的n个有序观察值，成为序列长度为n的观察值序列。
应用时间序列分析的目的就是给定一个已被观测了的时间序列，预测该序列的未来值。
时间序列算法
常用的时间序列模型
| 模型名称 | 描述 |
|---|---|
| 平滑法 | 平滑法常用于趋势分析和预测，利用修匀技术，削弱短期随机波动对序列的影响，使序列平滑化。根据所用平滑技术的不同，可具体分为’移动平均’法和’指数平滑法’ |
| 趋势拟合法 | 趋势拟合法把时间作为自变量，响应的序列观察值作为因变量，建立回归模型，根据序列的特征，可具体分为线性拟合和曲线拟合 |
| 组合模型 | 时间序列的变化主要受长期趋势（T）、季节变动（S）、周期变动（C）、不规则变动（ε） 这四个因素的影响。根据时间序列的特点，可以构建加法模型和乘法模型：加法模型：xt=Tt+St+Ct+εt 乘法模型：xt=TtStCt*εt |
| AR模型 |  以前p期的序列值Yt-1，Yt-2,…,Yt-p为自变量、随机变量的取值Yt为因变量建立线性回归模型 |
| MA模型 |  随机变量的取值Y与以前各期的序列值无关，建立Y与前q期的随机扰动εt-1，εt-2,…,εt-q的线性回归模型 |
| ARMA模型 |  随机变量的取值与前p期的序列值和前q期的随机扰动都有关 |
| ARIMA模型 | 许多非平稳序列差分后悔显示出平稳序列的性质，称这个非平稳序列为差分平稳序列。 对差分平稳序列可以使用ARIMA进行拟合 |
| ARCH模型 | ARCH模型能准确地模拟时间序列变量的波动性的变化，适用于序列具有异方差性并且异方差函数短期自相关 |
| GARCH模型及衍生模型 | GARCH模型成为广义ARCH模型，是ARCH模型的拓展。相比ARCH更能反映实际序列中的长期记忆性、信息的非对称性 |
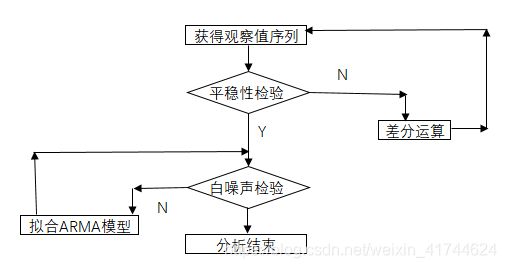
时间序列的预处理
拿到一个观察值序列后，首先要对它的纯随机性和平稳性进行检验，这两个重要的检验成为序列的预处理。
- 纯随机序列：白噪声序列，序列的各项之间没有任何相关关系，序列在进行完全无序的随机波动，可以终止对该序列的分析。 白噪声序列是没有信息可提取的平稳序列
- 平稳非白噪声序列：它的均值和方差为常数，通常是建立一个线性模型拟合该序列，ARMA模型是常用的平稳序列拟合模型
- 非平稳序列：由于均值和方差不稳定，处理方法一般是转换为平稳序列，然后再应用平稳时间序列分析法（ARMA）。如果一个时间序列经差分运算后平稳，则为差分平稳序列，使用（ARIMA）
平稳性检验
(1)平稳时间序列的定义
知识：
对于随机变量X，可以计算均值（数学期望）μ、方差σ²；
对于两个随机变量X、Y，可以计算X、Y的协方差COV（X,Y）=【(X-μx)(Y-μy)】和相关系数ρ(X,Y)=COV（X,Y）/σxσy，他们度量了两个事件之间的相互影响程度
对于时间序列{Xt，t∈T}在某一常数附近波动且波动范围有限，即有常数均值和常数方差，则可以定义时间序列{Xt}的自协方差函数COV（t,s）和自相关系数ρ(t,s)，t\s∈T，它们衡量同一时间在两个不同时间（t和s）之间的相关程度
结论：
如果时间序列{Xt，t∈T}在某一常数附近波动且波动范围有限，即有常数均值和常数方差，并且延迟k期的序列变量的自协方差和自相关系数是相等的，或者说延迟k期的序列变量之间影响程度是一样的，则称{Xt，t∈T}为平稳序列
(2)平稳时间序列的检验
- 根据时序图和自相关图的特征做出判断的图检验
- 根据构造检验统计量进行检验的方法（单位根检验）
时序图检验
根据平稳时间序列的均值和方差都是常数的性质，平稳序列的时序图显示该序列值始终都在一个常数附近波动，而且波动的范围有界；如果有明显趋势或者周期，通常不是平稳的
自相关图检验
平稳序列具有短期相关性，表明通常只有近期的序列值对现时值的影响比较明显，间隔远的过去值影响较小。随之延迟期数k的增加，平稳序列的自相关系数ρk会比较快的衰减趋于0，并在0附近随机波动，而非平稳的序列自相关系数衰减慢
(3)单位根的检验
检验序列中是否存在单位根，如果存在就是非平稳时间序列
纯随机性检验
如果是纯随机序列，它的序列值之间应该没有任何关系，满足相关系数等于0，这是理论上才会出现的理想状态，平常只是很接近0
纯随机性检验也叫白噪声检验，一般是构造检验统计量来检验序列的纯随机性，常用的检验统计量有：Q统计量、LB统计量
有样本各延迟期数的自相关系数可以计算得到检验统计量，然后算出对应的P值，如P值大于显著性水平α。则表示该序列不能拒绝纯随机原假设，可以停止分析
平稳时间序列分析
AR模型
以前p期的序列值Yt-1，Yt-2,…,Yt-p为自变量、认为主要受过去p期的序列值影响。误差项是当期的随机干扰εt（为零均值白噪声序列）
平稳AR模型的性质：
| 统计量 | 性质 |
|---|---|
| 均值 | 常数均值 |
| 方差 | 常数方差 |
| 自相关系数（ACF） | 拖尾 |
| 偏自相关系数（PACF） | p阶拖尾 |
MA模型
随机变量的取值Y与以前各期的序列值无关，建立Y与前q期的随机扰动εt-1，εt-2,…,εt-q的线性回归模型，误差项是当期的随机干扰εt（为零均值白噪声序列），μ是序列的均值。认为Yt主要受过去q期的误差项影响
平稳MA模型的性质：
| 统计量 | 性质 |
|---|---|
| 均值 | 常数均值 |
| 方差 | 常数方差 |
| 自相关系数（ACF） | q阶拖尾 |
| 偏自相关系数（PACF） | 拖尾 |
ARMA模型
随机变量的取值与前p期的序列值和前q期的随机扰动都有关，q为0是AR模型，p为0是MA模型
平稳ARMA模型的性质：
| 统计量 | 性质 |
|---|---|
| 均值 | 常数均值 |
| 方差 | 常数方差 |
| 自相关系数（ACF） | 拖尾 |
| 偏自相关系数（PACF） | 拖尾 |
平稳时间序列建模
- 计算ACF和PACF。先计算非平稳白噪声序列的自相关系数（ACF）和偏相关系数（PACF）
- ARMA模型识别定阶。由AR、MA和ARMA的自相关系数和偏自相关系数性质，选取合适的模型
- 估计模型中未知参数的值并进行参数检验
- 模型检验
- 模型优化（不通过则重新识别定阶）
- 模型应用：短期预测
非平稳时间序列分析
非平稳时间序列分析可以分为确定性因素分解的时序分析和随机时序分析两类
- 确定因素分解：把变化归结为四个因素（长期趋势、季节变动、循环变动、随机波动），其中长期趋势和季节变动的规律性信息通常比较容易提取，而由随机因素导致的波动则非常难确定和分析，浪费随机信息会导致模型精度不理想。
- 随机时序分析：为了弥补确定因素分析不足，有ARIMA模型、残差自回归模型、季节模型、异方差模型等
举例:ARIMA非平稳时间序列建模
导入数据
import pandas as pd
data = pd.read_excel('路径/arima_data.xls',index_col=u'日期')
forecastnum = 5
检验模型序列的平稳性–差分前
时序图：
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus'] = False
data.plot()
plt.show()
不在常数附近波动，呈现趋势，不平稳
自相关图：
# 自相关图
import statsmodels.api as sm
sm.graphics.tsa.plot_acf(data).show()
没有较快的趋于0，而是呈现缓慢的波动，不平稳
平稳性检测：
# 平稳性检测
statsmodels.tsa.stattools import adfuller as ADF
print(u'原始序列的ADF检测结果： ',ADF(data[u'销量']))
返回值依次为adf、pvalue、usedlag、nobs、critical values、from
P-value不接近0,大于显著性水平α，所以接受0假设，即存在单根
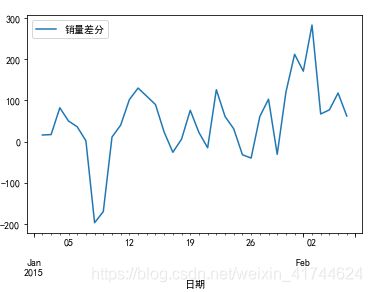
检验模型序列的平稳性–差分后
差分：
D_data = data.diff().dropna()
D_data.columns = [u'销量差分']
时序图：
D_data.plot()
plt.show()
在常数附近波动，范围有界，平稳
自相关图：
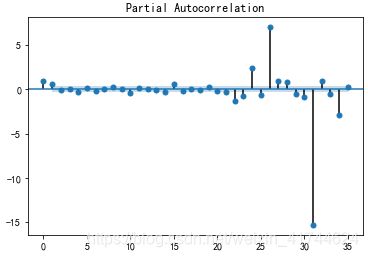
sm.graphics.tsa.plot_acf(D_data).show()
迅速接近于0并波动，平稳
偏相关图：
sm.graphics.tsa.plot_pacf(D_data).show
偏相关图同理
平稳性检测：
print(u'差分序列的ADF检验结果为：',ADF(D_data[u'销量差分']))
P值小于显著性水平α，拒绝原假设，不存在单根，平稳
返回值依次为adf、pvalue、usedlag、nobs、critical values、from
白噪声检验（纯随机性检验）
from statsmodels.stats.diagnostic import acorr_ljungbox
print(u'差分序列的白噪声检验结果为： ' ,acorr_ljungbox(D_data,lags=1))
stat=11.3 P值=0.007 所以差分后是平稳非白噪声序列
定阶
采用相对最优模型识别：当p和q均小于等于3的所有组合BIC信息量最小的模型阶数：
from statsmodels.tsa.arima_model import ARIMA
# 定阶
pmax = int(len(D_data)/10)
qmax = int(len(D_data)/10)
bic_matrix = []
for p in range(pmax+1):
tmp = []
for q in range(qmax+1):
try:
tmp.append(ARIMA(data,(p,1,q)).fit().bic)
except:
tmp.append(None)
bic_matrix.append(tmp)
bic_matrix = pd.DataFrame(bic_matrix)
p,q = bic_matrix.stack().idxmin()
print (u'BIC最小的p值和q值为： %s、 %s' %(p,q))
定阶完毕：
用AR（1）模型拟合一阶差分后的序列，即对原序列建立ARIMA（0,1,1）模型。模型非唯一，检验ARIMA（1,1,0）和ARIMA（1,1,1）这两个模型都可以通过检验
建模
model = ARIMA(data,(p,1,q)).fit()
model.summary2()
魔性的参数检验和估计如下图：
应用ARIMA（0,1,1）对data中的数据做其之后五天的预测：
model.forecast(5)
