【数学建模笔记 24】数学建模的时间序列模型

24. 时间序列模型

定义

时间序列是按时间顺序排列的、随时间变化且相互关联的数据序列。分析时间序列的方法构成数据分析的一个重要领域，即时间序列分析。

一个时间序列往往是以下几类变化形式的叠加。

• 长期趋势变动 $T_t$：朝一定方向的变化趋势；
• 季节变动 $S_t$；
• 循环变动 $C_t$：周期一年以上，由非季节因素引起的涨落起伏波形相似的波动；
• 不规则变动 $R_t$。

常见的确定性时间序列模型有

• 加法模型 $y_t=T_t+S_t+C_t+R_t$​；
• 乘法模型 $y_t=T_t\cdot S_t\cdot C_t\cdot R_t$​；
• 混合模型。

其中 $y_t$ 是目标的观测记录，$E(R_t)=0,E(R_t^2)={\sigma }^2$。

移动平均法

当时间序列由于受周期变动和不规则变动的影响，起伏较大，不易显示出发展趋势时，可用移动平均法消除这些因素的影响。

简单移动平均法

设观测序列为 $y_1,\dots ,y_T$，取移动平均项数 $N<T$，一次简单移动平均值计算公式为
$$M_t^{(1)}=\frac{1}{N}(y_t+y_{t-1}+\cdots +y_{t-N+1})$$

$$=M_{t-1}^{(1)}+\frac{1}{N}(y_t-t_{t-N}).$$

令 ${\hat{y}}_{t+1}=M_t^{(1)}$，得到预测模型，并有误差
$$S=\sqrt{\frac{{\sum }_{t=N+1}^T({\hat{y}}_t-y_t{)}^2}{T-N}}.$$

加权移动平均法

设时间序列为 $y_1,\dots ,y_t,\dots$，加权移动平均公式为
$$M_{tw}=\frac{w_1{y}_t+w_2{y}_2+\cdots +w_N{y}_{t-n+1}}{w_1+w_2+\cdots +w_N},t\ge N,$$
其中 $M_{tw}$ 为 $t$ 期加权移动平均数，$w_i$ 为 $y_{t-i+1}$ 的权数，得预测公式
$${\hat{y}}_{t+1}=M_{tw}.$$

趋势移动平均法

一次移动得平均数为
$$M_t^{(1)}=\frac{1}{N}(y_t+y_{t-1}+\cdots +y_{t-N+1}),$$
在一次移动平均的基础上再进行一次移动平均，就是二次移动平均，计算公式为
$$M_t^{(2)}=\frac{1}{N}(M_t^{(1)}+\cdots +M_{t-N+1}^{(1)})$$

$$=M_{t-1}^{(2)}+\frac{1}{N}(M_t^{(1)}-M_{t-N}^{(1)}).$$

设时间序列某时期开始具有直线趋势，则设
$${\hat{y}}_{t+T}=a_t+b_{t}T,T=1,2,\dots$$
则有
$$a_t=y_t,y_{t-1}=y_t-b_t,y_{t-2}=y_t-2b_t,$$

$$\dots$$

$$y_{t-N+1}=y_t-(N-1)b_t.$$

故
$$M_t^{(1)}=\frac{N{y}_t-[1+\cdots +(N-1)b_t]}{N}$$

$$=y_t-\frac{N-1}{2}{b}_t.$$

即
$$y_t-M_t^{(1)}=\frac{N-1}{2}{b}_t,$$
同理有
$$y_{t-1}-M_{t-1}^{(1)}=\frac{N-1}{2}{b}_{t-1},$$
故
$$y_t-y_{t-1}=M_t^{(1)}-M_{t-1}^{(1)}=b_t,$$
同理有
$$M_t^{(1)}-M_t^{(2)}=\frac{N-1}{2}{b}_t,$$
于是有
$$\{\begin{array}{rl}& a_t=2M_t^{(1)}-M_t^{(2)},\\ & b_t=\frac{2}{N-1}(M_t^{(1)}-M_t^{(2)}).\end{array}$$
一次移动平均实际上认为最近 N 期数据对未来影响相同，而 N 期以前的数据对未来没有影响。高阶移动平均则认为两端项权数小，中间项权数大，是对称的。

指数平滑法

一般说来，历史数据对未来的影响是递减的，指数平滑法可满足这一要求。

一次指数平滑法

设时间序列 $y_1,y_2,\dots ,y_t$，$\alpha$ 为加权系数，一次指数平滑公式为
$$S_t^{(1)}=\alpha y_t+(1-\alpha )S_{t-1}^{(1)}$$

$$=S_{t-1}^{(1)}+\alpha (y_t-S_{t-1}^{(1)}).$$

将式展开，有
$$S_t^{(1)}=\alpha y_t+(1-\alpha )[\alpha y_{t-1}+(1-\alpha )S_{t-2}^{(1)}]$$

$$=\cdots =\alpha \sum _{j=0}^{\infty }(1-\alpha {)}^j{y}_{t-j}.$$

表明 $S_t^{(1)}$ 是全部历史数据的加权平均，系数分别为 $\alpha ,\alpha (1-\alpha ),\alpha (1-\alpha {)}^2,\dots$，符合指数规律。

有预测模型
$${\hat{y}}_{t+1}=S_t^{(1)}=\alpha y_t+(1-\alpha ){\hat{y}}_t.$$

二次指数平滑法

一次指数平滑法存在明显的滞后偏差，可以再作二次指数平滑，有
$$S_t^{(1)}=\alpha y_t+(1-\alpha )S_{t-1}^{(1)},$$

$$S_t^{(2)}=\alpha S_t^{(1)}+(1-\alpha )S_{t-1}^{(2)}.$$

设时间序列从某时期开始具有直线趋势，可得
$${\hat{y}}_{t+T}=a_t+b_{t}T,T=1,2,\dots$$

$$\{\begin{array}{rl}& a_t=2S_t^{(1)}-S_t^{(2)},\\ & b_t=\frac{\alpha }{1-\alpha }(S_t^{(1)}-S_t^{(2)}).\end{array}$$

三次指数平滑法

时间序列变动表现为二次曲线趋势时，需要用三次指数平滑法，即
$$S_t^{(1)}=\alpha y_t+(1-\alpha )S_{t-1}^{(1)},$$

$$S_t^{(2)}=\alpha S_t^{(1)}+(1-\alpha )S_{t-1}^{(2)}.$$

$$S_t^{(3)}=\alpha S_t^{(2)}+(1-\alpha )S_{t-1}^{(3)}.$$

预测模型为
$${\hat{y}}_{t+T}=a_t+b_{t}T+C_t{T}^2,T=1,2,\dots$$

$$\{\begin{array}{rl}& a_t=3S_t^{(1)}-3S_t^{(2)}+S_t^{(3)},\\ & b_t=\frac{\alpha }{2(1-\alpha {)}^2}[(6-5\alpha )S_t^{(1)}\\ & -2(5-4\alpha )S_t^{(2)}+(4-3\alpha )S_t^{(3)}],\\ & c_t=\frac{{\alpha }^2}{2(1-\alpha {)}^2}[S_t^{(1)}-2S_t^{(2)}+S_t^{(3)}].\end{array}$$

差分指数平滑法

当时间序列变动具有直线趋势时，用一次指数平滑法会出现滞后偏差。可以先对源数据进行差分，构成一个平稳的新序列 (消除直线趋势)，再使用指数平滑法预测，再与变量当前实际值迭加作为预测值。
$$\nabla y_t=y_t-y_{t-1},$$

$$\nabla {\hat{y}}_{t+1}=\alpha \nabla y_t+(1-\alpha )\nabla {\hat{y}}_t,$$

$${\hat{y}}_{t+1}=\nabla {\hat{y}}_{t+1}+y_t.$$

同样的，当时间序列呈现二次曲线增长时，可用二阶差分指数平滑模型预测
$$\nabla y_t=y_t-y_{t-1},$$

$${\nabla }^2{y}_t=\nabla y_t-\nabla y_{t-1}$$

$${\nabla }^2{\hat{y}}_{t+1}=\alpha {\nabla }^2{y}_t+(1-\alpha ){\nabla }^2{\hat{y}}_t,$$

$${\hat{y}}_{t+1}={\nabla }^2{\hat{y}}_{t+1}+\nabla y_t+y_t.$$

自适应滤波法

基本预测公式为
$${\hat{y}}_{t+1}=w_1{y}_t+w_2{y}_{t-1}+\cdots +w_N{y}_{t-N+1}$$

$$=\sum _{i=1}^N{w}_i{y}_{t-i+1}.$$

调整权数的公式为
$$w_i=w_i+2k\cdot e_{i+1}{y}_{t-i+1}.$$
其中 $k$ 为学习常数，$e_{i+1}$ 为第 $t+1$ 期预测误差。

步骤：

1. 设定初始权数、学习常数和开始时期 $t$；
2. 根据预测公式计算 $t+1$ 期的预测值 ${\hat{y}}_{t+1}$；
3. 计算预测误差 $e_{t+1}=y_{t+1}-{\hat{y}}_{t+1}$；
4. 根据调整公式更新权数；
5. $t$ 进 1，回到步骤 2，直到 $t$ 超出序列的最后一个时期，迭代结果。

季节性时间序列预测

使用季节系数法，步骤如下：

1. 计算每年所有季度的算数平均值
   $$\overline{a}=\frac{1}{k}\sum _{i=1}^m\sum _{j=1}^n{a}_{ij},k=mn,$$
   其中 $i,j$ 分别表示年份、季度的序号；

2. 计算同季度的算数平均值
   $${\overline{a}}_{\cdot j}=\frac{1}{m}\sum _{i=1}^m{a}_{ij},j=1,2,\dots ,n,$$

3. 计算季度系数 $b_j={\overline{a}}_{\cdot j}/\overline{a}$​；

4. 预测下一年的年加权平均
   $${\overline{y}}_{m+1}=\frac{{\sum }_{i=1}^m{w}_i{y}_i}{n{\sum }_{i=1}^n{w}_i},$$

5. 得到各季度的预测值
   $$y_{m+1,j}=b_j{\overline{y}}_{m+1}.$$

ARMA 时间序列

设随机序列 $\{X_t,t=0,\pm 1,\pm 2,\dots \}$ 满足

• $E(X_t)=\mu =\text{常数}$​，
• ${\gamma }_{t+k,t}={\gamma }_k$ 与 $t$​ 无关，

则称 $X_t$ 为平稳序列。

ARMA 序列，即自回归移动平均序列，由两部分组成：

• AR 序列

$$X_t={\varphi }_1{X}_{t-1}+{\varphi }_2{X}_{t-2}+\cdots +{\varphi }_p{X}_{t-p}+{\epsilon }_t,$$

其中 ${\epsilon }_t$ 是均值为 0，方差为 ${\sigma }_{\epsilon }^2$ 的平稳白噪声，称 $X_t$ 是阶数为 $p$ 的自回归序列，记 $AR(p)$。

• MA 序列

$$X_t={\epsilon }_t-{\theta }_1{\epsilon }_{t-1}-{\theta }_2{\epsilon }_{t-2}-\cdots -{\theta }_q{\epsilon }_{t-q},$$

其中 ${\epsilon }_t$ 是均值为 0，方差为 ${\sigma }_{\epsilon }^2$ 的平稳白噪声，称 $X_t$ 是阶数为 $q$ 的移动平均序列，记 $MA(q)$。

于是有
$$X_t-{\varphi }_1{X}_{t-1}+{\varphi }_2{X}_{t-2}+\cdots +{\varphi }_p{X}_{t-p}$$

$$={\epsilon }_t-{\theta }_1{\epsilon }_{t-1}-{\theta }_2{\epsilon }_{t-2}-\cdots -{\theta }_q{\epsilon }_{t-q},$$

其中 ${\epsilon }_t$ 是均值为 0，方差为 ${\sigma }_{\epsilon }^2$ 的平稳白噪声，称 $X_t$ 是阶数为 $p,q$ 的自回归移动平均序列，记 $ARMA(p,q)$。

模型构建

AIC 准则：选 $p,q$ 使得
$$\min AIC=n\ln {\hat{\sigma }}_{\epsilon }^2+2(p+q+1),$$
其中 $n$ 是样本容量，${\hat{\sigma }}_{\epsilon }^2$ 是 ${\sigma }_{\epsilon }^2$ 的估计值。​

参数估计

可以使用矩估计、最小二乘估计、最大似然估计等方法。

模型预测

记 $X_{k+m}$ 的估计量为 ${\hat{X}}_k(m)$，对于 AR 序列
$$\{\begin{array}{rl}& {\hat{X}}_k(1)={\varphi }_1{X}_k+{\varphi }_2{X}_{k-1}+\cdots +{\varphi }_p{X}_{k-p+1},\\ & {\hat{X}}_k(2)={\varphi }_1{\hat{X}}_k(1)+{\varphi }_2{X}_k+\cdots +{\varphi }_p{X}_{k-p+2},\\ & \dots \\ & {\hat{X}}_k(m)={\varphi }_1{\hat{X}}_k(m-1)+{\varphi }_2{\hat{X}}_k(m-2)+\cdots +{\varphi }_p\hat{X}(m-p),m>p.\end{array}$$
对于 MA 序列，有
$$\{\begin{array}{rl}& {\hat{X}}_{k+1}(1)={\theta }_1{\hat{X}}_k(1)+{\hat{X}}_k(2)-{\theta }_1{X}_{k+1},\\ & {\hat{X}}_{k+1}(2)={\theta }_2{\hat{X}}_k(1)+{\hat{X}}_k(3)-{\theta }_2{X}_{k+1},\\ & \dots \\ & {\hat{X}}_{k+1}(q)={\theta }_q{\hat{X}}_k(1)+{\hat{X}}_k(q)-{\theta }_q{X}_{k+1}.\end{array}$$
令 ${\hat{X}}_k^{(q)}=({\hat{X}}_k(1),\dots ,{\hat{X}}_k(q){)}^T$，得
$${\hat{X}}_{k+1}^{(q)}=\left(\begin{array}{cccccc}{\theta }_1& 1& 0& \dots & 0& \\ {\theta }_2& 0& 1& \dots & 0& \\ ⋮& ⋮& \ddots & ⋮& ⋮& \\ {\theta }_{q-1}& 0& 0& \dots & 1& \\ {\theta }_q& 0& 0& \dots & 0& \end{array}\right){\hat{X}}_k^{(q)}-\left(\begin{array}{c}{\theta }_1\\ {\theta }_2\\ ⋮\\ {\theta }_q\end{array}\right)X_{k+1.}$$
可取初值 ${\hat{X}}_{k_0}^{(q)}=0$​，当 $n$​ 充分大后，初始误差的影响逐渐消失。

因此对于 ARMA 序列，令
$${\varphi }_j^{\ast }=\{\begin{array}{rl}& {\varphi }_j,j=1,2,\dots ,p,\\ & 0,j>p.\end{array}$$
有递推式
$${\hat{X}}_{k+1}^{(q)}=\left(\begin{array}{cccccc}-G_1& 1& 0& \dots & 0& \\ -G_2& 0& 1& \dots & 0& \\ ⋮& ⋮& \ddots & ⋮& ⋮& \\ -G_{q-1}& 0& 0& \dots & 1& \\ -G_q+{\varphi }_q^{\ast }& {\varphi }_{q-1}^{\ast }& {\varphi }_{q-2}^{\ast }& \dots & {\varphi }_1^{\ast }& \end{array}\right){\hat{X}}_k^{(q)}$$

$$+\left(\begin{array}{c}{G}_1\\ G_2\\ ⋮\\ G_q\end{array}\right)X_{k+1}+\left(\begin{array}{c}0\\ 0\\ ⋮\\ {\sum }_{j=q+1}^p{\varphi }_j^{\ast }{X}_{k+q+1-j}\end{array}\right).$$

其中 $G_j$ 满足 $X_t={\sum }_{j=0}^{\infty }{G}_j{\epsilon }_{t-j}$，可令初值 ${\hat{X}}_{k_0}^{(q)}=0$。

ARIMA 模型

对差分运算后得到的平稳序列用 ARMA 模型拟合，称 $ARIMA(p,d,q)$ 模型，其中 $p,d,q$ 分别表示 $AR$ 的项数、差分阶数、$MA$ 的项数。

Python 代码

二次指数平滑法

对某厂钢产量作预测，数据如下

t	钢产量	一次平滑	二次平滑	预测值
1	2031	2031	2031
2	2234	2091.9	2049.27	2031
3	2566	2234.13	2104.728	2152.8
4	2820	2409.891	2196.277	2418.99
5	3006	2588.724	2314.011	2715.054
6	3093	2740.007	2441.81	2981.171
7	3277	2901.105	2579.598	3166.002
8	3514	3084.973	2731.211	3360.4
9	3770	3290.481	2898.992	3590.348
10	4107	3535.437	3089.925	3849.752
11				4171.882
12				4362.815

输出如下：

#! /usr/bin/env python
# -*- coding: utf-8 -*-
# @ author: Koorye
# @ date:
# @ function: ARIMA 模型

# %%

import numpy as np
import pandas as pd

# %%

# 源数据
df = pd.DataFrame({
    't': [i for i in range(1, 11)],
    'production': [2031, 2234, 2566, 2820, 3006,
                   3093, 3277, 3514, 3770, 4107],
})

# 设 alpha=.3，计算一次、二次指数平滑
alpha = .3
s1, s2 = [int(df['production'][0])],\
    [int(df['production'][0])]

for i in range(1, len(df['t'])):
	s1.append(alpha*df['production'][i] + (1-alpha)*s1[i-1])
	s2.append(alpha*s1[i] + (1-alpha)*s2[i-1])
df['s1'] = s1
df['s2'] = s2

# %%

# 计算过去年的预测值，以及未来年的线性表达式
predict_list = [None]
for i in range(len(df['t'])-1):
	a = 2*df['s1'][i] - df['s2'][i]
	b = (alpha / (1-alpha)) * (df['s1'][i] - df['s2'][i])
	predict_list.append(a + b)

t = 10
a = 2*df['s1'][t-1] - df['s2'][t-1]
b = (alpha / (1-alpha)) * (df['s1'][t-1] - df['s2'][t-1])
df['predict'] = predict_list
print('at =', a)
print('bt =', b)

# %%

# 计算未来年的预测值
pred_df = df.copy()
for i in range(5):
	pred_df = pd.concat([pred_df, pd.DataFrame({
		't': [10+i+1],
		'predict': a + b*i,
	})])
pred_df

# %%

# 画图
import matplotlib.pyplot as plt

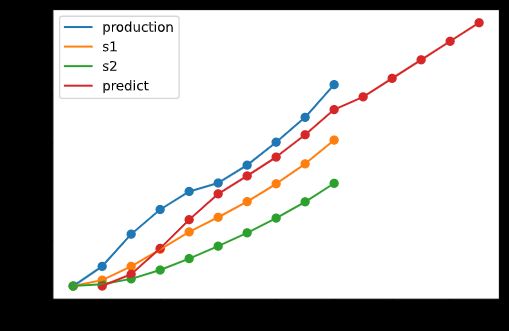
plt.plot(pred_df['t'], pred_df['production'],label='production')
plt.scatter(pred_df['t'], pred_df['production'])
plt.plot(pred_df['t'], pred_df['s1'],label='s1')
plt.scatter(pred_df['t'], pred_df['s1'])
plt.plot(pred_df['t'], pred_df['s2'],label='s2')
plt.scatter(pred_df['t'], pred_df['s2'])
plt.plot(pred_df['t'], pred_df['predict'],label='predict')
plt.scatter(pred_df['t'], pred_df['predict'])
plt.legend()

输出如下：

t	production	s1	s2	predict
0	1	2031.0	2031.000000	2031.000000	NaN
1	2	2234.0	2091.900000	2049.270000	2031.000000
2	3	2566.0	2234.130000	2104.728000	2152.800000
3	4	2820.0	2409.891000	2196.276900	2418.990000
4	5	3006.0	2588.723700	2314.010940	2715.054000
5	6	3093.0	2740.006590	2441.809635	2981.170500
6	7	3277.0	2901.104613	2579.598128	3166.002240
7	8	3514.0	3084.973229	2731.210659	3360.399591
8	9	3770.0	3290.481260	2898.991839	3590.348330
9	10	4107.0	3535.436882	3089.925352	3849.751862
0	11	NaN	NaN	NaN	3980.948412
0	12	NaN	NaN	NaN	4171.881925
0	13	NaN	NaN	NaN	4362.815438
0	14	NaN	NaN	NaN	4553.748951
0	15	NaN	NaN	NaN	4744.682464

ARMA 模型

根据 1971~1990 年的太阳黑子数量预测 1991~2000 年的太阳黑子数量，代码如下：

#! /usr/bin/env python
# -*- coding: utf-8 -*-
# @ author: Koorye
# @ date: 2021-7-29
# @ function: ARMA 模型

# %%

import numpy as np
import pandas as pd
import statsmodels.api as sm
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf
import matplotlib.pyplot as plt

# %%

# 源数据
df = pd.DataFrame({
    'year': [i for i in range(1971, 1991)],
    'num': [66.6, 68.9, 38, 34.5, 15.5,
            12.6, 27.5, 92.5, 155.4, 154.6,
            140.4, 115.9, 66.6, 45.9, 17.9,
            3.4, 29.4, 100.2, 157.6, 142.6],
})

# %%

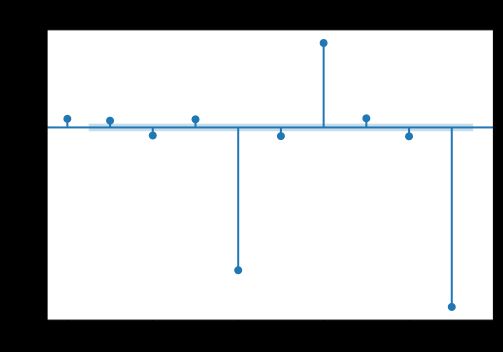
# 画 acf 图
plot_acf(df['num'])

# %%

# 画 pacf 图
plot_pacf(df['num'], lags=9)

# %%

# 建立模型，参考 acf、pacf 代入 p、q，观察 aic
str_list = []
for p in range(1, 6):
    for q in range(1, 3):
        model = sm.tsa.ARMA(df['num'], (p, q)).fit()
        str_list.append('p = {}, q = {}, aic = {}'.format(p, q, model.aic))

for each in str_list:
	print(each)

# %%

# 发现 p=2,q=2 时 aic 最小，取 p=2,q=2
model = sm.tsa.ARMA(df['num'], (2, 2)).fit()
model.summary()

# %%

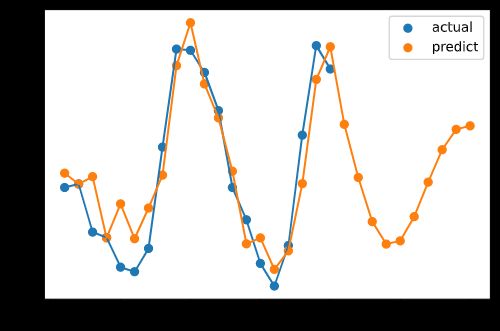
# 预测和画图
plt.plot(df['year'], df['num'])
plt.scatter(df['year'], df['num'], label='actual')
year_list = [i for i in range(1971, 2001)]
plt.plot(year_list, model.predict(0, len(year_list)-1))
plt.scatter(year_list, model.predict(0, len(year_list)-1), label='predict')
plt.legend()

输出如下：

p = 1, q = 1, aic = 194.84701061998135
p = 1, q = 2, aic = 194.31427174057512
p = 2, q = 1, aic = 188.97865479513626
p = 2, q = 2, aic = 188.92457119015984
p = 3, q = 1, aic = 191.31192040477467
p = 3, q = 2, aic = 192.40349950348713
p = 4, q = 1, aic = 193.19411553305596
p = 4, q = 2, aic = 193.1505615705116
p = 5, q = 1, aic = 194.3858472180579
p = 5, q = 2, aic = 194.78028983920348

Dep. Variable:	num	No. Observations:	20
Model:	ARMA(2, 2)	Log Likelihood	-88.462
Method:	css-mle	S.D. of innovations	17.694
Date:	Thu, 29 Jul 2021	AIC	188.925
Time:	22:06:42	BIC	194.899
Sample:	0	HQIC	190.091

	coef	std err	z	P>|z|	[0.025	0.975]
const	75.7977	3.130	24.217	0.000	69.663	81.932
ar.L1.num	1.5399	0.106	14.571	0.000	1.333	1.747
ar.L2.num	-0.8567	0.104	-8.245	0.000	-1.060	-0.653
ma.L1.num	-0.5612	0.339	-1.658	0.097	-1.225	0.102
ma.L2.num	-0.4386	0.291	-1.509	0.131	-1.008	0.131

	Real	Imaginary	Modulus	Frequency
AR.1	0.8987	-0.5996j	1.0804	-0.0936
AR.2	0.8987	+0.5996j	1.0804	0.0936
MA.1	1.0001	+0.0000j	1.0001	0.0000
MA.2	-2.2796	+0.0000j	2.2796	0.5000

ARIMA 模型

对 austa 数据集使用 ARIMA 模型作预测，代码如下：

#! /usr/bin/env python
# -*- coding: utf-8 -*-
# @ author: Koorye
# @ date:
# @ function: ARIMA 模型

# %%

import numpy as np
import pandas as pd
from statsmodels.tsa.arima_model import ARIMA
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf
import matplotlib.pyplot as plt

# %%

# 源数据
df = pd.DataFrame({
    'year': [i for i in range(1980, 2011)],
    'val': [0.82989428, 0.85951092, 0.87668916, 0.86670716, 0.932052,
            1.04826364, 1.3111932, 1.63756228, 2.0641074, 1.91268276,
            2.03544572, 2.17721128, 2.38968344, 2.75059208, 3.0906664,
            3.42664028, 3.83064908, 3.97190864, 3.83160036, 4.143101,
            4.566551, 4.47541, 4.462796, 4.384829, 4.796861,
            5.046211, 5.098759, 5.196519, 5.166843, 5.174744,
            5.440894],
})

# %%

# 作一阶差分
df['val_diff1'] = df['val'].diff()
plt.plot(df['year'], df['val'])
plt.plot(df['year'], df['val_diff1'])

# %%

# ACF 图
plot_acf(df['val_diff1'][1:])

# %%

# PACF 图
plot_pacf(df['val_diff1'][1:], lags=14)

# %%

# 参考 ACF 和 PCAF 代入 p,q
str_list = []
for p in range(1, 4):
    for q in range(0, 4):
        model = ARIMA(df['val'], order=(p, 1, q))
        res = model.fit(disp=0)
        str_list.append('p = {}, q = {}, aic = {}'.format(p, q, res.aic))
for each in str_list:
    print(each)

# %%

# p=2,q=0 使 aic 最小
model = ARIMA(df['val'], order=(2, 1, 0))
res = model.fit(disp=0)
res.summary()

# %%

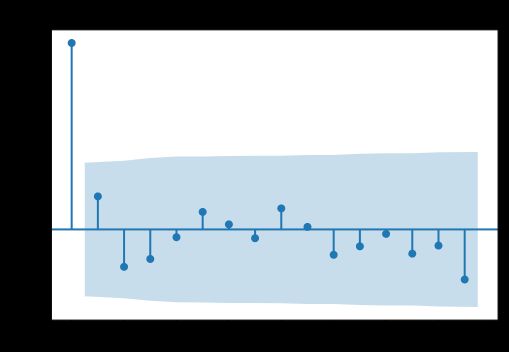
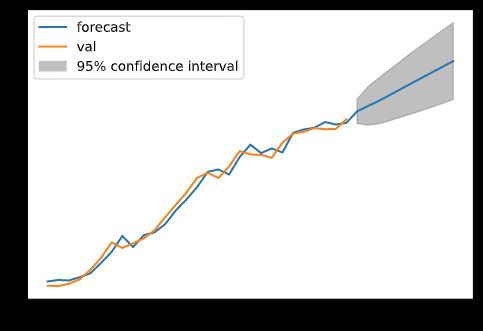
# 作预测图
res.plot_predict(end=40)

输出如下：

p = 1, q = 0, aic = -13.718554829816128
p = 1, q = 1, aic = -12.644935232547795
p = 1, q = 2, aic = -13.023448862467816
p = 1, q = 3, aic = -11.034475643866699
p = 2, q = 0, aic = -13.534487801792835
p = 2, q = 1, aic = -11.848263794395535
p = 2, q = 2, aic = -11.032058544143538
p = 2, q = 3, aic = -9.036565460115241
p = 3, q = 0, aic = -11.784035132385696
p = 3, q = 1, aic = -9.84986571141387
p = 3, q = 2, aic = -8.617052624191913
p = 3, q = 3, aic = -5.945170779675806