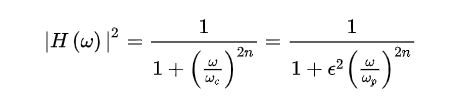基于matlab的巴特沃思数字滤波器设计,基于Matlab巴特沃斯低通滤波器的设计
基于Matlab巴特沃斯低通滤波器的设计
谢继杨
(成都理工大学工程技术学院,四川乐山,614000)
摘要:现如今已经有相当成熟的技术去模拟滤波器,人们为了更加深入的理解巴特沃斯滤波器,于是巴特沃斯模拟滤波器便基于matlab来编程。同时几种模拟滤波器将被我们用于比较。
关键词:MATLAB;巴特沃斯低通滤波器;相关滤波器的比较
Design of Butterworth low pass filter based onMatlab
ZuozheXiejiyang
(TheEngineering&TechnicalCollege of Chengdu University of technology,Leshan,Sichuan614000)
Abstract:Nowadays, there are quite mature technologies to simulate filters. In order to have a deeper understanding ofbutterworthfilters,butterworthanalog filters are programmed based on MATLAB. At the same time several analog filters will be used for comparison.
Keywords:MATLAB;Butterworth low pass filter;Comparison of correlation filters
1.引言:
MATLAB属于科学计算软件的一种,在工程应用领域用于分析设计和复杂计算,方便的使用,简洁的输入,高效的运算,丰富的内容是它的代名词,并且编写后可作函数文件的方式储存,调用相当简单。滤波器这种电子装置可以在有用频率信号通过的同时衰减无用频率。在频率高于一个确定数值的电路中,滤波器便起到了抑制作用。所以,巴特沃斯滤波器能使用matlab来高速便捷的编程模拟。
2正文:
2.1巴特沃斯滤波器的原理
在现代各式各样的滤波器设计方法中,巴特沃斯型滤波器是最为为人知晓的,之所以被推广应用的原因,是因为它很容易就被设计,性能优点比起缺点更为明显,元件Q值在滤波器中属于低水平,因此很好制造还能达到设计标准。其最为明显的地方当属于在通频带那最为平滑的频率响应曲线。
要想实现改变截止频率,就必须先将还没设计的滤波器截止频率比上基准滤波器的截止频率,使用计算出的比值M去比上这当中所有的元件值。其中M的计算公式为;M=还未设计滤波器的截止频率/基准滤波器的截止频率。
关于变换特征阻抗,要将待设计的滤波器的特征阻抗去除以基准滤波器的特征阻抗,得到比值K,接下来用K去与该滤波器中的所有的电容元件值相比以及与基准滤波器中所有的电感元件值相乘,便可实现。
2.2巴特沃斯滤波器的优点
在通频带内最大程度的平坦,不起伏,在阻频带则慢慢下降至零是频率响应的特点。从一个边界角频率开始角频率逐渐增加振幅随之减少并趋向负无穷则是在振幅的对数对角频率的波特图特点。
每种滤波器在高阶与低阶呈现的振幅对角频率不同,巴特沃斯滤波器不一样的地方便是阶数、振幅对角频率保持了同样形状,只是在阻频带振幅衰减速度与阶数成正比。最为直观的表现为一阶巴特沃斯滤波器的衰减率六分贝每倍频,二阶巴特沃斯滤波器衰减率十二分贝每倍频,三阶巴特沃斯的衰减率十八分贝每倍频,特别指出在一阶时每十倍频是二十分贝。
类比于切比雪夫滤波器,巴特沃斯滤波器有高通,低通,带通,带阻等多种滤波器分类设计。平稳的幅频特点,较为漫长的过渡带,让它在通频带中容易在过渡带失真,在仿真时第一周期往往会出现失真,随之往后的幅频特性越来越好。
2.3多种滤波器的比较
Bessel滤波器在线性过滤器中具有最为平坦的群延迟以及最为平坦的幅度和相位响应。因此在音频天桥系统中使用最为常用。每到模拟Bessel滤波器时恒定的群延迟便出现在通频带内并几乎将其横跨,所以过滤的信号波形在通频带上被保留。几乎呈线性的相位响应则属于用户常常关注的区域——带通。所以Bessel滤波器用于减少非线性相位失真在所有IIR滤波器中这一固有特点。
切比雪夫这一滤波器的特点是频率响应幅度等波纹波动,发生在通带或阻带上,等波纹这一振幅特点在通带上。被称为切比雪夫Ⅰ型的滤波器则是在阻带内单调的;被称为切比雪夫Ⅱ型的滤波器则在通带才是单调的,在阻带内却是等波纹的。所以如何选用切比雪夫滤波器得看实际情况采取合适的型号针对性选用。
椭圆滤波器滤波器也就是常说的Cauer滤波器,在阶数相同的情况下通带和阻带波动最小,而且在通带和阻带波动相同,这也正是它被区别于巴特沃斯滤波器和切比雪夫滤波器的特点。如果从传递函数的角度出发,常数除以多项式是巴特沃斯和切比雪夫滤波器的特点,表现为衰减为无限大当处于无限大阻带时。而Cauer滤波器既有零点也有极点,产生等波纹时极点与零点在通带内,有限的传输零点在阻带内时产生了让过渡区减少的情况,所以方便获得的衰减曲线非常陡峭,这便形成了Cauer最大优势,不过有利还是会存在弊端,如此陡峭的衰减曲线正是通过通带和阻带的不稳定来换取的。而且由于传输函数较之巴特沃斯和切比雪夫滤波器更为繁琐,如果使用传统设计思路,设计程序,过程计算极为复杂。
巴特沃斯、切比雪夫、贝塞尔和椭圆滤波器比较
3实例
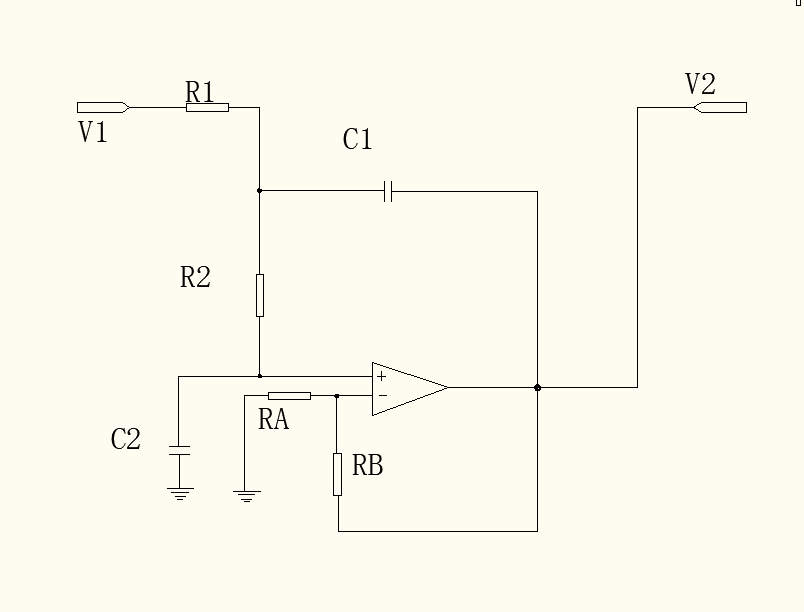
首先将巴特沃斯滤波器在matlab上模拟如下:
图3.1.1二阶有源电路图
一、巴特沃斯低通滤波器可用公式表示为:
图3.1.2
![]() =滤波器的阶数
=滤波器的阶数
![]() =截止频率=振幅下降为-3分贝时的频率
=截止频率=振幅下降为-3分贝时的频率
![]() =通频带边缘频率
=通频带边缘频率
二、为一个巴特沃斯低通滤波器设计技术标准:
通带截至频率fp=2.6kHz,
阻带截至频率fs=3.6kHz,
通带最大衰减2dB,
阻带最小衰减31dB。
三、在MATLAB中程序编写如下:
wp= 2*pi*2600;
ws= 2*pi*3600;
Rp= 2;
As = 31;
[N,wc] =buttord(wp,ws,Rp,As,'s');
[B, A] =butter(N,wc,'s');
fk=0:800/512:8000;
wk= 2*pi*fk;
HK =freqs(B,A,wk);
x =fk/1000;
y = 20*log10(abs(HK));
figure
plot(fk/1000, 20*log10(abs(HK)));
gridon,xlabel('频率(kHz)'),ylabel('幅度(dB)')
title('巴特沃斯模拟滤波器')
axis([0,4,-35,5])
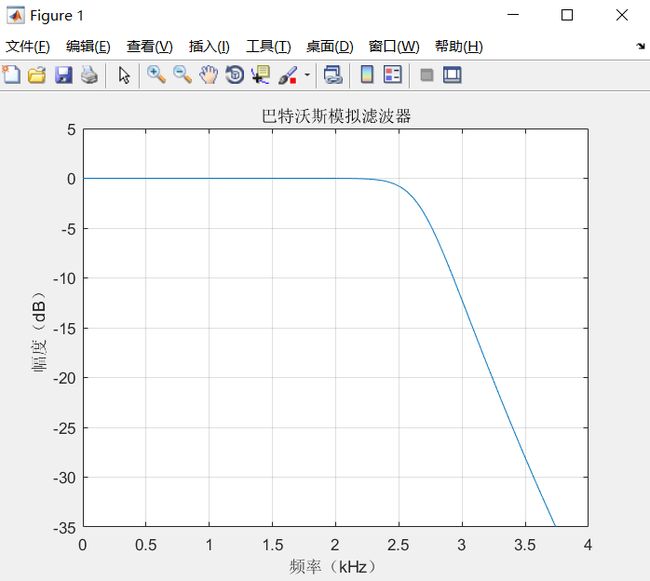
四、运行于MATLAB的结果
图3.1.4响应特性对于巴特沃斯低通滤波器的显示
验证结果
经仿真得到结果:
巴特沃斯滤波器随着频率升高幅度单调变化,图像平顺,波纹稳定不起伏。完全符合巴特沃斯滤波器特点,实例仿真成功。
4总结
Matlab的运用大大简化了设计过程,降低了设计成本,不仅按照要求设计出了满足指标的巴特沃斯滤波器,还通过波特图显示出了其幅频曲线,严谨的事实依据为其验证提高了可靠性,体现了科学性,推动了巴特沃斯滤波器的各项研究进程,为以后深入研究打下了牢固基础。
参考文献:
[1]吴忻生,唐萍,秦瀚.数字滤波技术在称重系统信号采集中的应用[J].传感器与微系统,2010,29(09):131-134.
[2]张小虹.数字信号处理[M].北京:机械工业出版社,2008.