拉格朗日乘子法
- 周志华《机器学习》
- 如何理解拉格朗日乘子法?
1. 介绍
拉格朗日乘子法 (Lagrange multipliers)是一种寻找多元函数在一组约束下的极值的方法。通过引入拉格朗日乘子,可将有 d d d 个变量与 k k k 个约束条件的最优化问题转化为具有 d + k d + k d+k 个变量的无约束优化问题求解。
2. 相关知识
2.1 与原点的最短距离
假如有方程 x 2 y = 3 x^2y=3 x2y=3,它的图像如下(左一)所示。现在我们想求其上点与原点的最短距离(中图)。这里介绍一种解题思路。首先,与原点距离为 a a a 的点全部在半径为 a a a 的圆上(右一):
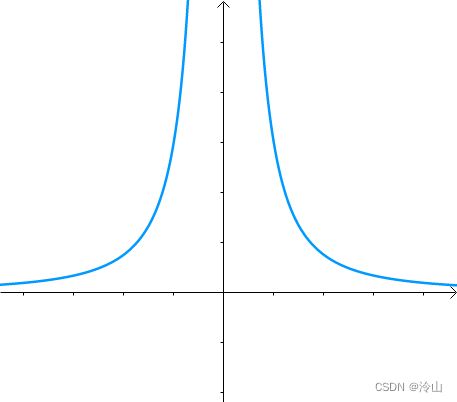
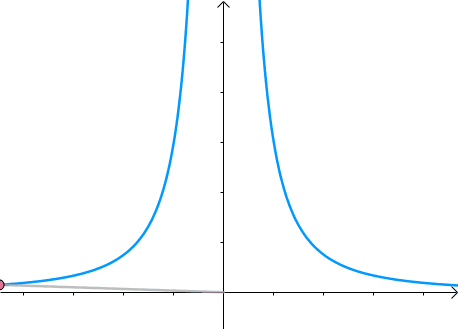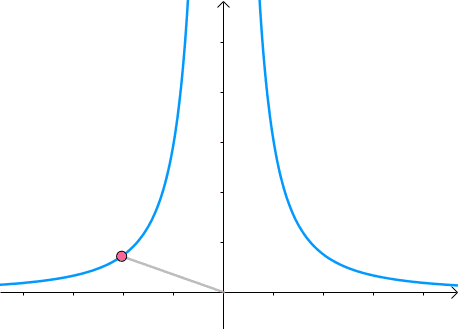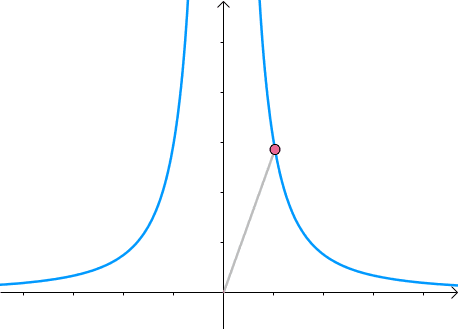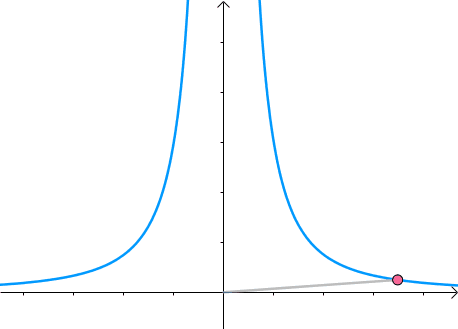

那么,我们逐渐扩大圆的半径(左一)。显然,第一次与 x 2 y = 3 x^2y=3 x2y=3 相交的点就是距离原点最近的点(中图),此时,圆和曲线相切,也就是在该点切线相同(右一):
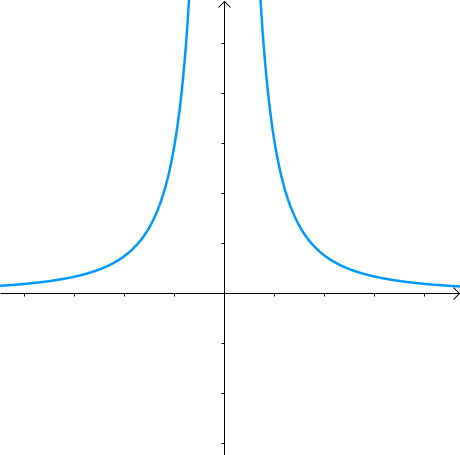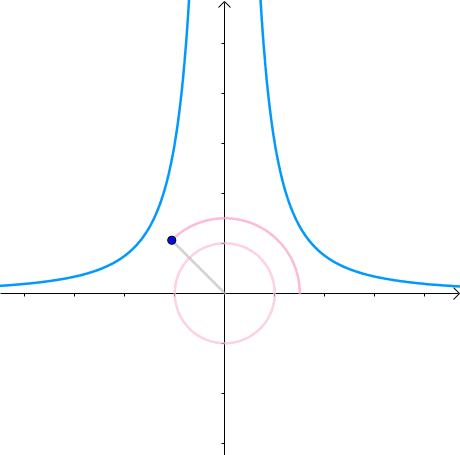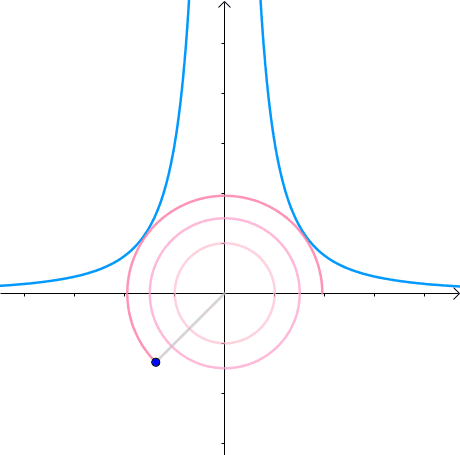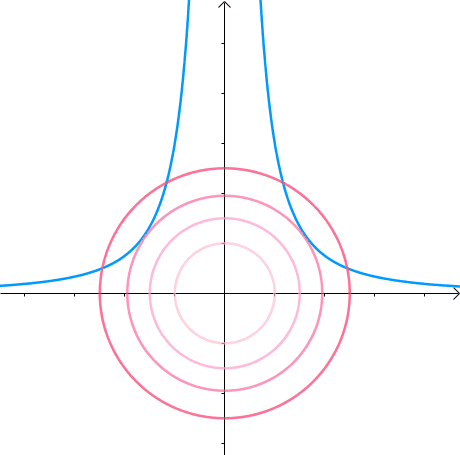
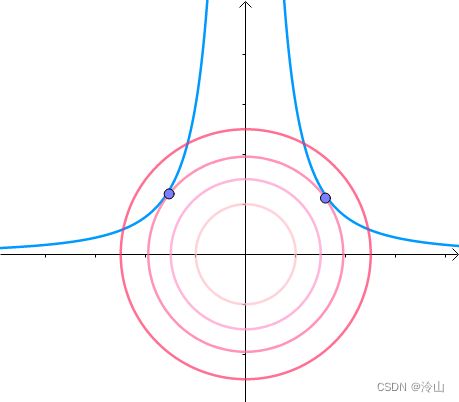
至此,我们分析出了:在极值点,圆与曲线相切。
2.2 等高线/等值线
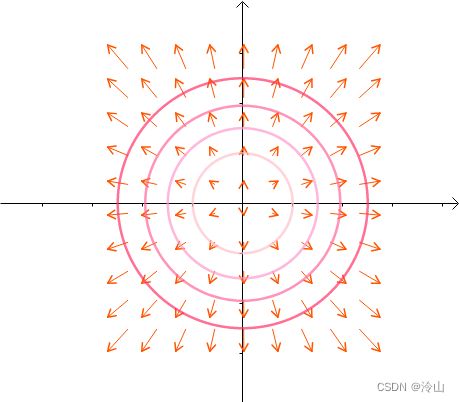
这里引入等高线的概念。这些同心圆(左一),可以看作函数 f ( x , y ) = x 2 + y 2 f(x,y)=x^2+y^2 f(x,y)=x2+y2 (如广泛使用的二范数,普遍会被作为约束条件)的等高线(中图),根据梯度的性质,梯度向量:
∇ f = ( ∂ f ∂ x ∂ f ∂ y ) = ( 2 x 2 y ) \nabla f=\left(\begin{array}{l} \frac{\partial f}{\partial x} \\ \frac{\partial f}{\partial y} \end{array}\right)=\left(\begin{array}{l} 2 x \\ 2 y \end{array}\right) ∇f=(∂x∂f∂y∂f)=(2x2y)
是等高线的法线(右一):

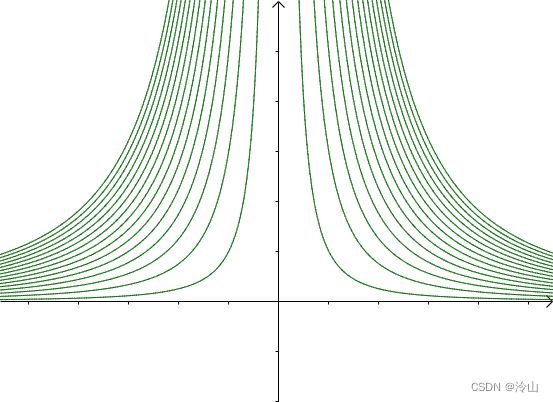
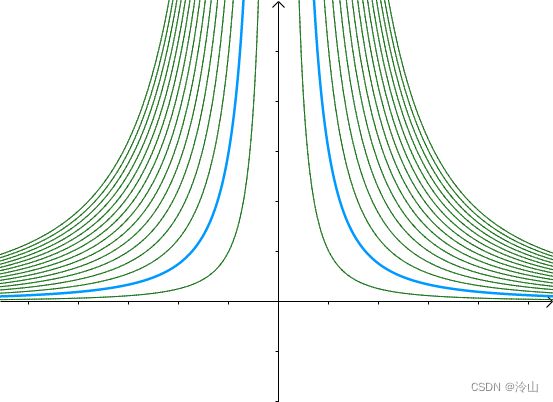
另外一个函数 g ( x , y ) = x 2 y g(x,y)=x^2y g(x,y)=x2y 的等高线为左一,之前的曲线 x 2 y = 3 x^2y=3 x2y=3 就是其中值为 3 3 3 的等高线(中图),因此梯度向量:
∇ g = ( ∂ g ∂ x ∂ g ∂ y ) = ( 2 x y x 2 ) \nabla g=\left(\begin{array}{c} \frac{\partial g}{\partial x} \\ \frac{\partial g}{\partial y} \end{array}\right)=\left(\begin{array}{c} 2 x y \\ x^{2} \end{array}\right) ∇g=(∂x∂g∂y∂g)=(2xyx2)
也垂直于等高线 x 2 y = 3 x^2y=3 x2y=3(右一):
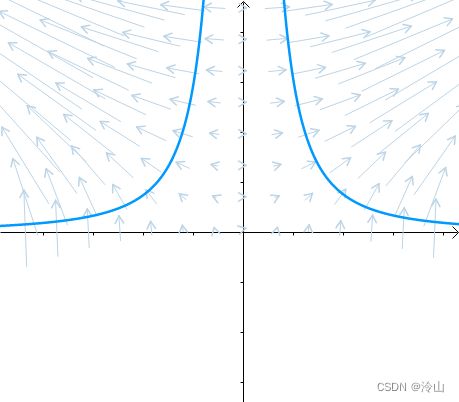
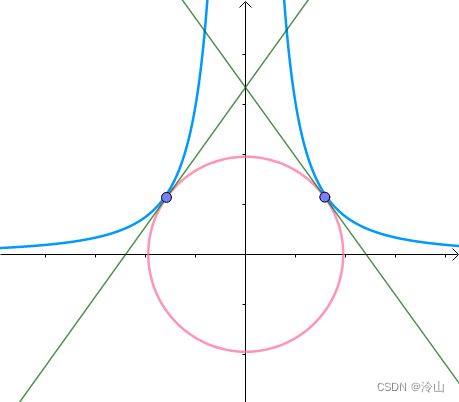
梯度向量是等高线的法线,更准确地表述是:梯度与等高线的切线垂直。
2.3 小结
综上,得到两个结论:
- 在极值点,圆与曲线相切
- 梯度与等高线的切线垂直
综合可知,在相切点,圆的梯度向量和曲线的梯度向量平行。也就是梯度向量平行,用数学符号表示为 ∇ f = λ ∇ g \nabla f=\lambda \nabla g ∇f=λ∇g:
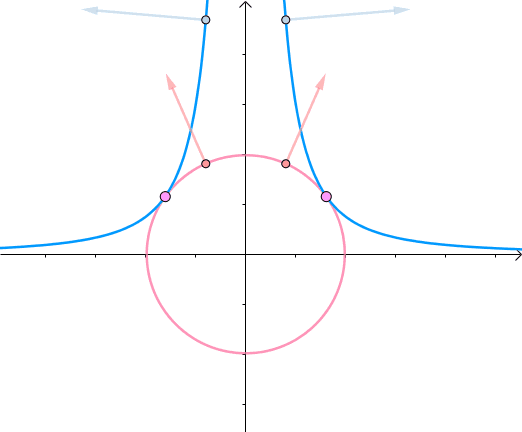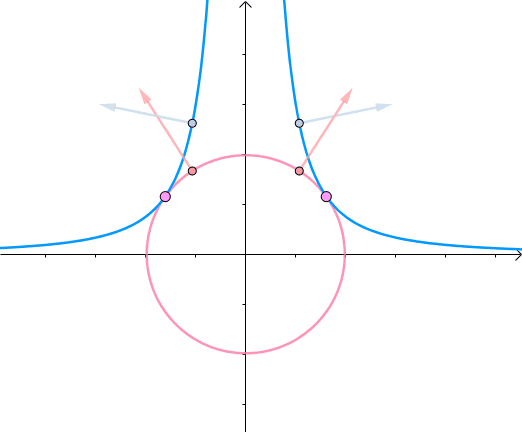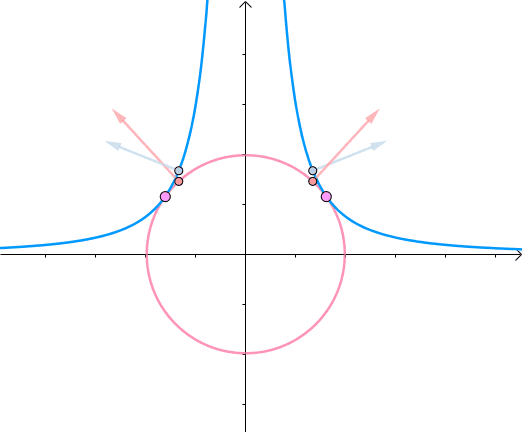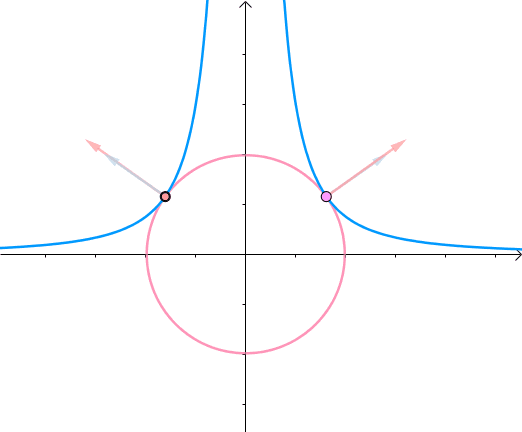
3. 约束
3.1 等式约束
先考虑一个等式约束的优化问题:假定 x \boldsymbol{x} x 为 d d d 维向量,欲寻找 x \boldsymbol{x} x 的某个取值 x ∗ \boldsymbol{x}^* x∗,使目标函数 f ( x ) f(x) f(x) 最小且同时满足 g ( x ) = 0 g(x) = 0 g(x)=0 的约束。从几何角度看,该问题的目标是在由方程 g ( x ) = 0 g(x) = 0 g(x)=0 确定的 d − 1 d-1 d−1 维曲面上寻找能使目标函数 f ( x ) f(x) f(x) 最小化的点此时不难得到如下结论:
- 对于约束曲面上的任意点 x \boldsymbol{x} x , 该点的梯度 ∇ g ( x ) \nabla g(\boldsymbol{x}) ∇g(x) 正交于约束曲面(梯度与等高线切线垂直);
- 在最优点 x ∗ \boldsymbol{x}^* x∗,目标函数在该点的梯度 ∇ f ( x ∗ ) \nabla f(\boldsymbol{x}^*) ∇f(x∗) 正交于约束曲面(若梯度 ∇ f ( x ∗ ) \nabla f(\boldsymbol{x}^*) ∇f(x∗) 与约束曲面不正交,则仍可在约束曲面上移动该点使函数值进一步下降)。
由此可知,在最优点 x ∗ \boldsymbol{x}^* x∗,如附图B.1 所示,梯度 ∇ g ( x ) \nabla g(\boldsymbol{x}) ∇g(x) 和 ∇ f ( x ∗ ) \nabla f(\boldsymbol{x}^*) ∇f(x∗) 的方向必相同或相反,即存在 λ ≠ 0 \lambda \neq 0 λ=0 使得:
∇ f ( x ∗ ) + λ ∇ g ( x ∗ ) = 0 \nabla f\left(\boldsymbol{x}^{*}\right)+\lambda \nabla g\left(\boldsymbol{x}^{*}\right)=0 ∇f(x∗)+λ∇g(x∗)=0
λ \lambda λ 称为拉格朗日乘子(对等式约束, λ \lambda λ 可能为正也可能为负)。定义拉格朗日函数:
L ( x , λ ) = f ( x ) + λ g ( x ) L(\boldsymbol{x}, \lambda)=f(\boldsymbol{x})+\lambda g(\boldsymbol{x}) L(x,λ)=f(x)+λg(x)
不难发现,将其对 x \boldsymbol{x} x 的偏导数 ∇ x L ( x , λ ) \nabla_{\boldsymbol{x}} L(\boldsymbol{x}, \lambda) ∇xL(x,λ) 置零(=0)即得式 ∇ f ( x ∗ ) + λ ∇ g ( x ∗ ) = 0 \nabla f\left(\boldsymbol{x}^{*}\right)+\lambda \nabla g\left(\boldsymbol{x}^{*}\right)=0 ∇f(x∗)+λ∇g(x∗)=0,同时,将其对 λ 的偏导数 ∇ x L ( x , λ ) \nabla_{\boldsymbol{x}} L(\boldsymbol{x}, \lambda) ∇xL(x,λ) 置零即得约束条件 g ( x ) = 0 g(\boldsymbol{x}) = 0 g(x)=0。于是,原约束优化问题可转化为对拉格朗日函数 L ( x , λ ) L(\boldsymbol{x}, \lambda) L(x,λ) 的无约束优化问题。
3.1.1 示例
这里继续使用第二节中的示例,这里引入 x 2 y = 3 x^2y=3 x2y=3 这个约束条件,否则那么多等高线,不知道是哪一根,即 g ( x ) = x 2 y − 3 g(x)=x^2y-3 g(x)=x2y−3,而 f ( x ) = x 2 + y 2 f(x)=x^2+y^2 f(x)=x2+y2,联立方程:
{ ∇ f = λ ∇ g x 2 y = 3 \left\{\begin{array}{l} \nabla f=\lambda \nabla g \\ x^{2} y=3 \end{array}\right. {∇f=λ∇gx2y=3
解得:
{ ( 2 x 2 y ) = λ ( 2 x y x 2 ) x 2 y = 3 ⟹ { x ≈ ± 1.61 y ≈ 1.1 λ ≈ 0.87 \left\{\begin{array} { l } { ( \begin{array} { l } { 2 x } \\ { 2 y } \end{array} ) = \lambda ( \begin{array} { c } { 2 x y } \\ { x ^ { 2 } } \end{array} ) } \\ { x ^ { 2 } y = 3 } \end{array} \Longrightarrow \left\{\begin{array}{l} x \approx \pm 1.61 \\ y \approx 1.1 \\ \lambda \approx 0.87 \end{array}\right.\right. ⎩ ⎨ ⎧(2x2y)=λ(2xyx2)x2y=3⟹⎩ ⎨ ⎧x≈±1.61y≈1.1λ≈0.87
3.1.2 多个等式约束
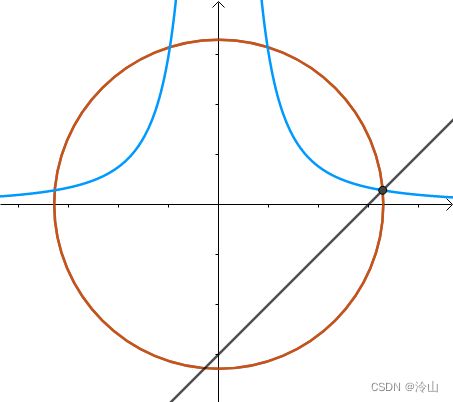
将上面的示例添加一个约束条件,如 x − y − 3 = 0 x-y-3=0 x−y−3=0,则变为了求解:
min x 2 + y 2 s.t. { x 2 y − 3 = 0 x − y − 3 = 0 \begin{array}{c} \min x^{2}+y^{2} \\ \text { s.t. }\left\{\begin{array}{l} x^{2} y-3=0 \\ x-y-3=0 \end{array}\right. \end{array} minx2+y2 s.t. {x2y−3=0x−y−3=0
从图上看约束条件是(左一)这样的,而很显然所求的距离如(中间)图片所示。那这三者的法线又有什么关系呢? x 2 + y 2 x^2+y^2 x2+y2 的法线是 x 2 y − 3 x^2y-3 x2y−3 和 x − y − 3 x-y-3 x−y−3 的法线的线性组合(右一蓝色法线画的有点问题?):

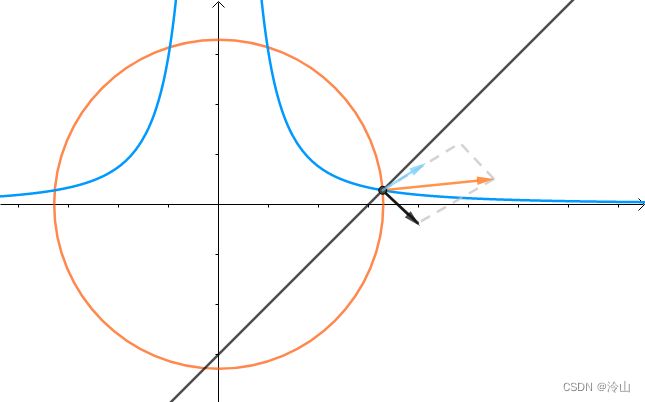
假设:
{ f ( x , y ) = x 2 + y 2 g 1 ( x , y ) = x 2 y − 3 g 2 ( x , y ) = x − y − 3 \left\{\begin{array}{l} f(x, y)=x^{2}+y^{2} \\ g_1(x, y)=x^{2} y-3 \\ g_2(x, y)=x-y-3 \end{array}\right. ⎩ ⎨ ⎧f(x,y)=x2+y2g1(x,y)=x2y−3g2(x,y)=x−y−3
那么线性组合就表示为:
∇ f = λ 1 ∇ g 1 + λ 2 ∇ g 2 \nabla f=\lambda_1 \nabla g_1+\lambda_2 \nabla g_2 ∇f=λ1∇g1+λ2∇g2
联立方程:
{ ∇ f = λ 1 ∇ g 1 + λ 2 ∇ g 2 g 1 ( x , y ) = 0 g 2 ( x , y ) = 0 \left\{\begin{array}{l} \nabla f=\lambda_1 \nabla g_1+\lambda_2 \nabla g_2 \\ g_1(x, y)=0 \\ g_2(x, y)=0 \end{array}\right. ⎩ ⎨ ⎧∇f=λ1∇g1+λ2∇g2g1(x,y)=0g2(x,y)=0
即可求解。
3.2 不等式约束
现在考虑不等式约束 g ( x ) ⩽ 0 g(\boldsymbol{x}) \leqslant 0 g(x)⩽0,如附图B.1 所示,此时最优点 x ∗ \boldsymbol{x}^* x∗ 或在 g ( x ) < 0 g(\boldsymbol{x}) < 0 g(x)<0 的区域中,或在边界 g ( x ) = 0 g(\boldsymbol{x}) = 0 g(x)=0 上。
- 对于 g ( x ) < 0 g(\boldsymbol{x}) < 0 g(x)<0 的情形, 约束 g ( x ) ⩽ 0 g(\boldsymbol{x}) \leqslant 0 g(x)⩽0 不起作用,可直接通过条件 ∇ f ( x ) = 0 \nabla f(x)=0 ∇f(x)=0 来获得最优点;这等价于将 λ \lambda λ 置零然后对 ∇ x L ( x , λ ) \nabla_{\boldsymbol{x}} L(\boldsymbol{x}, \lambda) ∇xL(x,λ) 置零得到最优点。
- g ( x ) = 0 g(x) = 0 g(x)=0 的情形类似于上面等式约束的分析,但需注意的是,此时 ∇ f ( x ∗ ) \nabla f(\boldsymbol{x}^*) ∇f(x∗) 的方向必与 ∇ g ( x ∗ ) \nabla g(\boldsymbol{x}^*) ∇g(x∗) 相反(下面小节会说明原因),即存在常数 λ > 0 \lambda>0 λ>0 使得 ∇ f ( x ∗ ) + λ ∇ g ( x ∗ ) = 0 \nabla f\left(\boldsymbol{x}^{*}\right)+\lambda \nabla g\left(\boldsymbol{x}^{*}\right)=0 ∇f(x∗)+λ∇g(x∗)=0。
3.2.1 上述两种情况示例
我们要求以下同心圆的最小值:

那肯定就是原点了,半径为 0 0 0 能得到最小值。
3.2.1.1 情况一
我们给它添加一个不等式约束,也就是求:
minimize f ( x , y ) subject to h ( x , y ) = x + y ≤ 1 \begin{aligned} & \text{minimize} & & f(x,y) \\ & \text{subject to} & & h(x,y)=x+y \le 1 \end{aligned} minimizesubject tof(x,y)h(x,y)=x+y≤1
可以看到,这个不等式约束实际上包含了原点:

所以这个约束等于没有,依然求解:
∇ f = 0 ⟹ ( x , y ) = ( 0 , 0 ) \nabla f=0\implies (x,y)=(0,0) ∇f=0⟹(x,y)=(0,0)
3.2.1.2 情况二
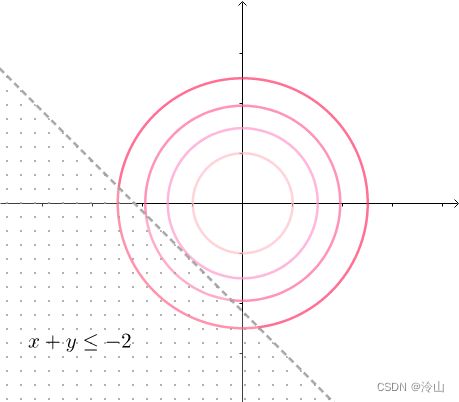
换一个不等式约束:
minimize f ( x , y ) subject to h ( x , y ) = x + y ≤ − 2 \begin{aligned} & \text{minimize} & & f(x,y) \\ & \text{subject to} & & h(x,y)=x+y \le -2 \end{aligned} minimizesubject tof(x,y)h(x,y)=x+y≤−2
不等式约束看起来如左一这样。因为同心圆是凸函数的等高线,所以等高线的值是(中图)这么排列的,在不等式约束下,最小值是在边缘相切的地方取得。这里和用等式 h ( x , y ) = x + y = − 2 h(x,y)=x+y=-2 h(x,y)=x+y=−2 进行约束效果是一样的:
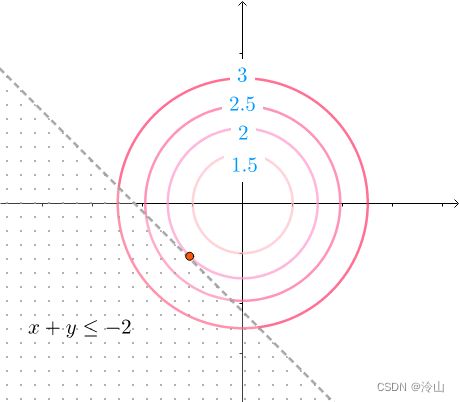
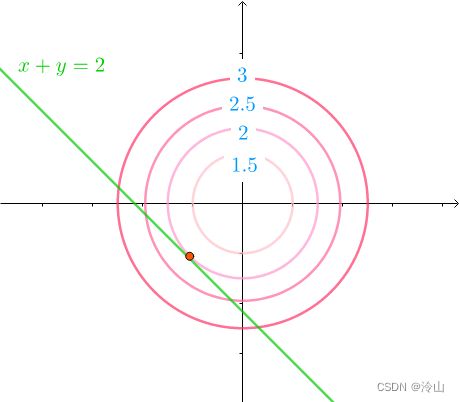
因此还是可以通过解方程组求出答案:
{ ∇ f + μ ∇ h = 0 h ( x , y ) = x + y = − 2 \begin{cases} \nabla f+\mu\nabla h=0 \\ h(x,y)=x+y=-2 \end{cases} {∇f+μ∇h=0h(x,y)=x+y=−2
可以发现不等式实际上带来了新的条件:同心圆是凸函数的等高线,等高线的值如下排列,所以在相切处,法线也就是 ∇ f \nabla f ∇f 的方向如下(法线也就是梯度,指向增长最快的方向,也就是等高线的值变大的方向)。而凸函数 h ( x , y ) h(x,y) h(x,y) 的法线 ∇ h \nabla h ∇h 也一样指向 h ( x , y ) h(x,y) h(x,y) 增长的方向,这个方向正好和 ∇ f \nabla f ∇f 相反:
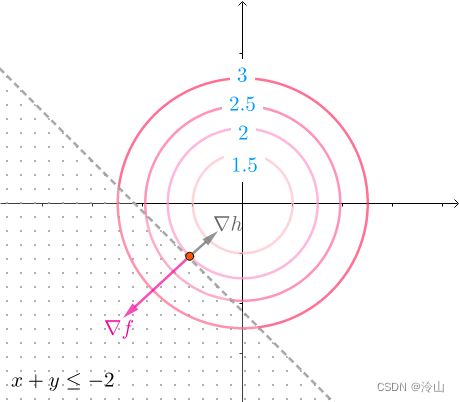
因此 ∇ f + μ ∇ h = 0 , μ ≥ 0 \nabla f+\mu\nabla h=0,\mu \ge 0 ∇f+μ∇h=0,μ≥0 其中, μ ≥ 0 \mu \ge 0 μ≥0 就表明 ∇ f \nabla f ∇f, ∇ h \nabla h ∇h 方向相反。
因此刚才的方程组可以再增加一个条件:
{ ∇ f + μ ∇ h = 0 h ( x , y ) = x + y = − 2 μ ≥ 0 \begin{cases} \nabla f+\mu\nabla h=0 \\ h(x,y)=x+y=-2 \\ \mu \ge 0 \end{cases} ⎩ ⎨ ⎧∇f+μ∇h=0h(x,y)=x+y=−2μ≥0
整合上面两种情形,必满足 λ g ( x ) = 0 \lambda g(\boldsymbol{x})=0 λg(x)=0。因此,在约束 g ( x ) ⩽ 0 g(\boldsymbol{x}) \leqslant 0 g(x)⩽0 下最小化 f ( x ) f(\boldsymbol{x}) f(x) ,可转化为在如下约束下最小化式 L ( x , λ ) = f ( x ) + λ g ( x ) L(\boldsymbol{x}, \lambda)=f(\boldsymbol{x})+\lambda g(\boldsymbol{x}) L(x,λ)=f(x)+λg(x) 的拉格朗日函数:
{ g ( x ) ⩽ 0 ; λ ⩾ 0 ; λ j g j ( x ) = 0. \left\{\begin{array}{l} g(\boldsymbol{x}) \leqslant 0 ; \\ \lambda \geqslant 0 ; \\ \lambda_{j} g_{j}(\boldsymbol{x})=0 . \end{array}\right. ⎩ ⎨ ⎧g(x)⩽0;λ⩾0;λjgj(x)=0.
该式被称为 Karush-Kuhn-Tucker(KKT)条件。
3.2.2 多个约束
上述做法可推广到多个约束。考虑具有 m m m 个等式约束和 n n n 个不等式约束,且可行域 D ⊂ R d \mathbb{D} \subset \mathbb{R}^{d} D⊂Rd 非空的优化问题:
Eq.1:
min x f ( x ) s.t. h i ( x ) = 0 ( i = 1 , … , m ) , g j ( x ) ⩽ 0 ( j = 1 , … , n ) . \begin{array}{ll} \min _{\boldsymbol{x}} & f(\boldsymbol{x}) \\ \text { s.t. } & h_{i}(\boldsymbol{x})=0 \quad(i=1, \ldots, m), \\ & g_{j}(\boldsymbol{x}) \leqslant 0 \quad(j=1, \ldots, n) . \end{array} minx s.t. f(x)hi(x)=0(i=1,…,m),gj(x)⩽0(j=1,…,n).
引入拉格朗日乘子 λ = ( λ 1 , λ 2 , … , λ m ) T \boldsymbol{\lambda}=\left(\lambda_{1}, \lambda_{2}, \ldots, \lambda_{m}\right)^{\mathrm{T}} λ=(λ1,λ2,…,λm)T 和 μ = ( μ 1 , μ 2 , … , μ n ) T \boldsymbol{\mu}=\left(\mu_{1}, \mu_{2}, \ldots, \mu_{n}\right)^{\mathrm{T}} μ=(μ1,μ2,…,μn)T,相应的拉格朗日函数为:
Eq.2:
L ( x , λ , μ ) = f ( x ) + ∑ i = 1 m λ i h i ( x ) + ∑ j = 1 n μ j g j ( x ) L(\boldsymbol{x}, \boldsymbol{\lambda}, \boldsymbol{\mu})=f(\boldsymbol{x})+\sum_{i=1}^{m} \lambda_{i} h_{i}(\boldsymbol{x})+\sum_{j=1}^{n} \mu_{j} g_{j}(\boldsymbol{x}) L(x,λ,μ)=f(x)+i=1∑mλihi(x)+j=1∑nμjgj(x)
由不等式约束引入的 KKT 条件( j = 1 , 2 , . . . , n j=1,2,...,n j=1,2,...,n)为:
{ ∇ f + ∑ i = 1 m λ i ∇ h i ( x ) + ∑ j = 1 n μ j ∇ g j ( x ) = 0 h i ( x ) = 0 , i = 1 , 2 , . . . , m g j ( x ) ⩽ 0 , j = 1 , 2 , . . . , n μ j ⩾ 0 μ j g j ( x ) = 0. \left\{\begin{array}{l} \nabla f+ \sum_{i=1}^{m} \lambda_{i} \nabla h_{i}(\boldsymbol{x})+\sum_{j=1}^{n} \mu_{j} \nabla g_{j}(\boldsymbol{x}) =0\\ h_{i}(\boldsymbol{x}) = 0, i=1,2,...,m \\ g_{j}(\boldsymbol{x}) \leqslant 0, j=1,2,...,n \\ \mu_{j} \geqslant 0 \\ \mu_{j} g_{j}(\boldsymbol{x})=0 . \end{array}\right. ⎩ ⎨ ⎧∇f+∑i=1mλi∇hi(x)+∑j=1nμj∇gj(x)=0hi(x)=0,i=1,2,...,mgj(x)⩽0,j=1,2,...,nμj⩾0μjgj(x)=0.
一个优化问题可以从两个角度来考察,即主问题(primal problem)和对偶问题(dual proble)。对主问题 Eq.1,基于式 Eq.2,其拉格朗日对偶函数(dual function) Γ : R m × R n ↦ R \Gamma: \mathbb{R}^{m} \times \mathbb{R}^{n} \mapsto \mathbb{R} Γ:Rm×Rn↦R 定义为:
Γ ( λ , μ ) = inf x ∈ D L ( x , λ , μ ) = inf x ∈ D ( f ( x ) + ∑ i = 1 m λ i h i ( x ) + ∑ j = 1 n μ j g j ( x ) ) \begin{aligned} \Gamma(\boldsymbol{\lambda}, \boldsymbol{\mu}) &=\inf _{\boldsymbol{x} \in \mathbb{D}} L(\boldsymbol{x}, \boldsymbol{\lambda}, \boldsymbol{\mu}) \\ &=\inf _{\boldsymbol{x} \in \mathbb{D}}\left(f(\boldsymbol{x})+\sum_{i=1}^{m} \lambda_{i} h_{i}(\boldsymbol{x})+\sum_{j=1}^{n} \mu_{j} g_{j}(\boldsymbol{x})\right) \end{aligned} Γ(λ,μ)=x∈DinfL(x,λ,μ)=x∈Dinf(f(x)+i=1∑mλihi(x)+j=1∑nμjgj(x))
在推导对偶问题时,常通过将拉格朗日乘子 L ( x , λ , μ ) L(\boldsymbol{x}, \boldsymbol{\lambda}, \boldsymbol{\mu}) L(x,λ,μ) 对 x \boldsymbol{x} x 求导并令导数为 0 0 0,来获得对偶函数的表达形式(是不是可以理解成,主问题是不带 λ \lambda λ 和 μ \mu μ 的,将主问题转换成带拉格朗日乘子的对偶问题,以方便求解)。
若 x ~ ∈ D \tilde{\boldsymbol{x}} \in \mathbb{D} x~∈D 为主问题 Eq.1 可行域中的点,则对任意 μ ⪰ 0 \boldsymbol{\mu} \succeq 0 μ⪰0 ( μ ⪰ 0 \boldsymbol{\mu} \succeq 0 μ⪰0 表示 μ \boldsymbol{\mu} μ 的分量均为非负)和 λ \boldsymbol{\lambda} λ 都有:
∑ i = 1 m λ i h i ( x ) + ∑ j = 1 n μ j g j ( x ) ⩽ 0 \sum_{i=1}^{m} \lambda_{i} h_{i}(\boldsymbol{x})+\sum_{j=1}^{n} \mu_{j} g_{j}(\boldsymbol{x}) \leqslant 0 i=1∑mλihi(x)+j=1∑nμjgj(x)⩽0
进而有:
Γ ( λ , μ ) = inf x ∈ D L ( x , λ , μ ) ⩽ L ( x ~ , λ , μ ) ⩽ f ( x ~ ) . \Gamma(\boldsymbol{\lambda}, \boldsymbol{\mu})=\inf _{\boldsymbol{x} \in \mathbb{D}} L(\boldsymbol{x}, \boldsymbol{\lambda}, \boldsymbol{\mu}) \leqslant L(\tilde{\boldsymbol{x}}, \boldsymbol{\lambda}, \boldsymbol{\mu}) \leqslant f(\tilde{\boldsymbol{x}}) . Γ(λ,μ)=x∈DinfL(x,λ,μ)⩽L(x~,λ,μ)⩽f(x~).
若主问题 Eq.1 的最优值为 p ∗ p^{*} p∗, 则对任意 μ ⪰ 0 \boldsymbol{\mu} \succeq 0 μ⪰0 和 λ \boldsymbol{\lambda} λ 都有
Γ ( λ , μ ) ⩽ p ∗ , \Gamma(\boldsymbol{\lambda}, \boldsymbol{\mu}) \leqslant p^{*}, Γ(λ,μ)⩽p∗,
即对偶函数给出了主问题最优值的下界( inf \inf inf).显然,这个下界取决于 μ \boldsymbol{\mu} μ 和 λ \boldsymbol{\lambda} λ 的值。于是,一个很自然的问题是:基于对偶函数能获得的最好下界是什么?这就引出了优化问题:
Eq.3:
max λ , μ Γ ( λ , μ ) s.t. μ ⪰ 0 \max _{\boldsymbol{\lambda}, \boldsymbol{\mu}} \Gamma(\boldsymbol{\lambda}, \boldsymbol{\mu}) \text { s.t. } \boldsymbol{\mu} \succeq 0 λ,μmaxΓ(λ,μ) s.t. μ⪰0
Eq.3 就是主问题 Eq.1 的对偶问题,其中 λ \boldsymbol{\lambda} λ 和 μ \boldsymbol{\mu} μ 称为对偶变量(dual variable)。无论主问题 Eq.1 的凸性如何,对偶问题 Eq.3 始终是凸优化问题。
考虑式 Eq.3 的最优值 d ∗ d^{*} d∗, 显然有 d ∗ ⩽ p ∗ d^{*} \leqslant p^{*} d∗⩽p∗, 这称为弱对偶性(weak duality)成立;若 d ∗ = p ∗ d^{*}=p^{*} d∗=p∗,则称为强对偶性(strong duality)成立,此时由对偶问题能获得主问题的最优下界。Eq.1。但是,若主问题为凸优化问题,如式 Eq.1 中 f ( x ) f(\boldsymbol{x}) f(x) 和 g j ( x ) g_{j}(\boldsymbol{x}) gj(x) 均为凸函数, h i ( x ) h_{i}(\boldsymbol{x}) hi(x) 为仿射函数,且其可行域中至少有一点使不等式约束严格成立,则此时强对偶性成立。值得注意的是,在强对偶性成立时,将拉格朗日函数分别对原变量和对偶变量求导,再并令导数等于零,即可得到原变量与对偶变量的数值关系。于是,对偶问题解决了,主问题也就解决了。
