【深度学习（deep learning）】花书第二章 线性代数 读书笔记

【深度学习（deep learning）】花书第二章 线性代数 读书笔记

---

前言

打基础，阅读花书，感觉一次性啃不动。看一点算一点，写一点笔记留作纪念。以便日后查看与回顾。第一章引言就不写了，从第二章开始。第二章回顾线性代数等数学基础。 日期：2020.11.17-2020.11.18

---

以下是正式内容。

一、基本概念

1. 标量（scalar）：一个数，小写+斜体表示。

2. 向量（vector）：一组数（通常是列向量，也就是一列数，可以看作是只有一列的矩阵）。有序排列，大小为数的个数，用n表示，可以按照标号索引。可以使用标号的子集 S或者标号的子集的补集 -S 同时索引多个元素。小写+粗体表示。向量中的元素用小写+斜体+脚标表示。

3. 矩阵（matrix）：二维数组。二维索引，分成 行 与 列。符号“:”代表整行或者整列。标量可以看作是1*1的矩阵。
   $${\mathbf{A}}_{m\times n}=\left[\begin{array}{cccc}{a}_{11}& a_{12}& \cdots & a_{1n}\\ a_{21}& a_{22}& \cdots & a_{2n}\\ ⋮& ⋮& \ddots & ⋮\\ a_{m1}& a_{m2}& \cdots & a_{mn}\end{array}\right]=\left[a_{ij}\right]$$

4. 张量（tensor）：三维及以上的数组（三维及以上的索引）。二维的张量是矩阵，一维的是向量。

二、矩阵运算

1. 转置：以对角线为轴的镜像翻转。特别地，对于标量a，
   $$a=a^{\text{T}}$$
2. 矩阵加法：对应元素相加。
3. 广播：矩阵加向量，将向量分别和矩阵的每一行相加。
4. 数乘：矩阵乘/加标量，每个元素都进行乘/加操作。
5. 矩阵乘积：矩阵乘法。可以分解为行和列的点积。
6. 矩阵元素对应乘积（Hadamard 乘积）：矩阵对应元素相乘。
   $$\mathbf{A}\odot \mathbf{B}=\left[\begin{array}{cccc}{a}_{11}\cdot b_{11}& a_{12}\cdot b_{12}& \cdots & a_{1n}\cdot b_{1n}\\ a_{21}\cdot b_{21}& a_{22}\cdot b_{22}& \cdots & a_{2n}\cdot b_{2n}\\ ⋮& ⋮& \ddots & ⋮\\ a_{m1}\cdot b_{m1}& a_{m2}\cdot b_{m2}& \cdots & a_{mn}\cdot b_{mn}\end{array}\right]$$
7. 点积：向量对应元素相乘后求和。即 $$x^{T}y$$
8. 矩阵乘积的性质：分配律，结合律，不满足交换律。点积满足交换律。
9. 求逆（逆矩阵运算）：满足
   $${\mathbf{A}}^{-1}\mathbf{A}=\mathbf{I}(\mathbf{E})$$
10. 行列式：将方阵映射到实数的函数。记作$$\det \left(\mathbf{A}\right)=\prod _i{\lambda }_i$$
    行列式的绝对值可以衡量矩阵参与乘法后空间扩大或收缩的程度，如果为0，则说明空间至少沿着某一维完全收缩（不满秩，对应向量组存在线性相关）。如果为1，则保持空间体积不变。
11. 迹运算：矩阵对角元素之和。特别地，矩阵连乘中，循环变换矩阵位置，运算结果矩阵的迹不变。 标量的迹是其本身。
    $$Tr\left(\mathbf{A}\right)=\sum _i{\mathbf{A}}_{i,i}$$$$Tr\left(\mathbf{A}\right)=Tr\left({\mathbf{A}}^T\right)$$
12. 正交：两个向量的内积为0，则两向量相互正交。
13. 标准正交：两向量正交，且都为模都为1.

三、特殊矩阵与向量

• 单位矩阵：主对角元素为1，其余为0.
  $${\mathbf{I}}_3=\left[\begin{array}{ccc}1& & \\ & 1& \\ & & 1\end{array}\right]$$

• 对角矩阵：主对角元素含非零元素，其余为0.
  $$\mathbf{D}\stackrel{\text{def}}{}\text{diag}\left(a_1,a_2,\cdots ,a_n\right)=\left[\begin{array}{cccc}l{a}_1& & & \\ & a_2& & \\ & & \ddots & \\ & & & a_n\end{array}\right]$$

• 对称矩阵：
  $$\mathbf{A}={\mathbf{A}}^{\text{T}}$$

• 实对称矩阵：元素为实数，且对称。

• 单位向量：模（范数）为1的向量。长度为1.
  $$\Vert x{\Vert }_2=1$$

• 正交矩阵：行向量和列向量分别标准正交的方阵。求逆很好求。
  $${\mathbf{A}}^{-1}\mathbf{A}=I$$$${\mathbf{A}}^{-1}={\mathbf{A}}^{\text{T}}$$

• 正定矩阵：所有特征值全都是正数的矩阵。保证：
  $$\forall \mathbf{x},{\mathbf{x}}^{\text{T}}\mathbf{A}\mathbf{x}\ge 0$$$${\mathbf{x}}^{\text{T}}\mathbf{A}\mathbf{x}=0\Rightarrow \mathbf{x}=0$$

• 半正定矩阵：所有特征值都是非负数的矩阵。保证：
  $$\forall \mathbf{x},{\mathbf{x}}^{\text{T}}\mathbf{A}\mathbf{x}\ge 0$$

• 负定（半负定）矩阵：所有特征值都是负数（非正数）的矩阵。

四、范数

范数(norm)来衡量向量的大小。将向量映射到非负值的函数。

• Lp 范数定义为：p>=1
  $$\Vert x{\Vert }_p={\left(\sum _i{\left|x_i\right|}^p\right)}^{\frac{1}{p}}$$
• L2范数：欧几里得范数。表示到原点的欧几里得距离。二维图像是一个圆。常计算平方L2范数。
  $$\Vert x{\Vert }_2^2=\Vert x{\Vert }^2=x^{T}x$$
• L1范数：用于区分零与非零元素时常用，希望获得稀疏解的时候使用。作为非零元素数目的替代函数。
  $$\Vert x{\Vert }_1=\sum _i\left|x_i\right|$$
• L0范数：非零元素的个数。不严格的定义。
• L∞范数：也称最大范数，表示具有最大幅值的元素的绝对值。
  $$\Vert x{\Vert }_{\infty }=\underset{i}{\max }\left|x_i\right|$$
• Frobenius 范数（Frobenius norm）：衡量矩阵大小的范数。类似向量的L2范数形式。
  $$\Vert \mathbf{A}{\Vert }_F=\sqrt{\sum _{i,j}{A}_{i,j}^2}=\sqrt{Tr(\mathbf{A}{\mathbf{A}}^T)}$$

五、特征分解与奇异值分解

1.特征分解

将矩阵分解成一组特征向量与特征值。
特征方程（特征值λ与特征向量v）的定义：
$$\mathbf{A}\mathbf{v}=\lambda \mathbf{v}$$
矩阵是奇异的，当且仅当含有零特征值。
将A的n个线性无关的特征向量拼成V，对应的特征值拼成对角矩阵diag（λ），则矩阵A的特征分解记作：
$$\mathbf{A}=\mathbf{V}\text{diag}\left(\mathbf{\lambda }\right){\mathbf{V}}^{-1}$$
实对称矩阵都可以进行特征值分解，分解成实特征值与实特征向量。且特征向量矩阵可为正交矩阵。特征值分解并不唯一，特征方程有重根时，任意一组正交的特征向量都可以。
$$\mathbf{A}=\mathbf{Q}\Lambda {\mathbf{Q}}^T$$

2.奇异值分解（SVD）

将矩阵分解为奇异向量与奇异值。获得信息与特征值类似，但是每一个实数矩阵都具有奇异值分解。（D是对角矩阵，但不一定是方阵，对角元素被称为奇异值）
$${\mathbf{A}}^{m\times n}={\mathbf{U}}^{m\times m}{\mathbf{D}}^{m\times n}({\mathbf{V}}^T{)}^{n\times n}$$
U的列向量称为左奇异向量，V的列向量是右奇异向量。A的非零奇异值是A与A的转置的乘积的特征值的平方根，有：
$$\mathbf{A}{\mathbf{A}}^T=\mathbf{U}\mathbf{D}{\mathbf{V}}^T\mathbf{V}{\mathbf{D}}^T{\mathbf{U}}^T=\mathbf{U}{\mathbf{\Sigma }}^2{\mathbf{U}}^T$$$${\mathbf{A}}^T\mathbf{A}=\mathbf{V}\mathbf{D}{\mathbf{U}}^T\mathbf{U}{\mathbf{D}}^T{\mathbf{V}}^T=\mathbf{V}{\mathbf{\Sigma }}^2{\mathbf{V}}^T$$

3.伪逆

对于不能求逆的矩阵A，依旧希望通过求逆运算，求解方程Ax=y，得到x=By。则希望伪逆运算定义一个将A映射到B的过程。
Moore-Penrose 伪逆：
定义式：
$${\mathbf{A}}^{+}=\underset{\alpha \searrow 0}{\lim }{\left({\mathbf{A}}^T\mathbf{A}+\alpha \mathbf{I}\right)}^{-1}{\mathbf{A}}^T$$
计算式：
$${\mathbf{A}}^{+}=\mathbf{V}{\mathbf{D}}^{+}{\mathbf{U}}^T$$
D+是对角矩阵D非零元素取倒数再转置得到的。
当A的列数多于行数，方程可能有去穷多解，则伪逆运算求得的解是所有可行解中欧几里得范数最小的一个。
当A的行数多于列数，方程可能没有解，这种情况下求得的x使得Ax和y的欧几里得距离最小。

六、主成分分析 PCA

对数据进行有损压缩，用一个低维表示去编码。使用矩阵乘法进行编码f(x)=c与解码（重构）g( c)=Dc。PCA是由解码函数而定的。为了使问题有唯一解，固定向量的模，使D的所有列向量都有单位范数。为了计算方便，限制D的列向量彼此正交。

1.如何根据x得到最优编码c*
最小化原始向量与重构向量之间的距离。使用L2距离的平方。
$${\mathbf{c}}^{\ast }=\text{arg}\underset{c}{\min }\Vert \mathbf{x}-g\left(\mathbf{c}\right){\Vert }_2^2$$$${\left(\mathbf{x}-g\left(\mathbf{c}\right)\right)}^T\left(\mathbf{x}-g\left(\mathbf{c}\right)\right)={\mathbf{x}}^T\mathbf{x}-2{\mathbf{x}}^{T}g\left(\mathbf{c}\right)+g{\left(\mathbf{c}\right)}^{T}g\left(\mathbf{c}\right)$$
忽略与c无关的x项，再带入g( c)的定义
$${\mathbf{c}}^{\ast }=\text{arg}\underset{c}{\min }-2{\mathbf{x}}^{T}g\left(\mathbf{c}\right)+g{\left(\mathbf{c}\right)}^{T}g\left(\mathbf{c}\right)=\text{arg}\underset{c}{\min }-2{\mathbf{x}}^T\mathbf{D}\mathbf{c}+{\mathbf{c}}^T\mathbf{c}$$
对上式关于c求导，令其为0，得到
$$\mathbf{c}={\mathbf{D}}^T\mathbf{x}，即f(\mathbf{x})={\mathbf{D}}^T\mathbf{x}$$
则PCA的重构操作为：$$r(\mathbf{x})=\mathbf{D}{\mathbf{D}}^T\mathbf{x}$$

2.找到合适的编码矩阵D
最小化原始向量与重构向量之间的距离。$${\mathbf{D}}^{\ast }=\text{arg}\underset{D}{\min }\Vert \mathbf{x}-r\left(\mathbf{x}\right){\Vert }_2^2$$
同时考虑所有样本和所有维数，即最小化Frobenius 范数
$${\mathbf{D}}^{\ast }=\text{arg}\underset{D}{\min }\Vert {\mathbf{X}-\mathbf{D}\mathbf{D}}^T\mathbf{X}{\Vert }_F=\sqrt{\sum _{i,j}(x_j^{(i)}-r(x^{(i)}{)}_j{)}^2}s.t.{\mathbf{D}}^T\mathbf{D}=\mathbf{I}$$

考虑一维向量，即D=d，得到最优d的目标是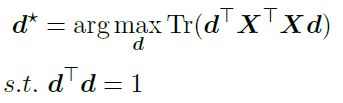
该式通过特征值分解求解，即d应该是其最大特征值对应的特征向量。
这样就得到了第一个主成分。也就是只用一个维度表示信息，且最大保留信息的那个维度。当扩展成l维时，有前L个最大的特征值对应的特征向量组成。

这个推导过程，貌似就是西瓜书PCA部分，注释中提到的 逐一选取最大主成分 的过程。

参考资料

1.机器学习，周志华
2.统计学习方法，第二版，李航
3.https://zhuanlan.zhihu.com/p/38431213
4.https://github.com/MingchaoZhu/DeepLearning
5.https://www.bilibili.com/video/BV1kE4119726?p=5