Control-车辆动力学模型

动力学主要研究作用于物体的力与物体运动的关系，车辆动力学模型一般用于分析车辆的平顺性和车辆操纵性的稳定性。对于车辆动力学，主要是研究车辆轮胎及相关部件的受力情况。比如纵向速度控制通过控制轮胎转速实现，横向航向控制通过控制轮胎转角实现。

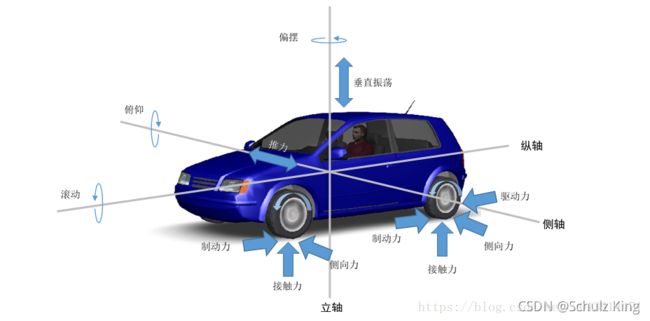
正常情况下，车辆上的作用力沿着三个不同的轴分布：

• $x$轴上的力：驱动力、制动力、滚动阻力和拖曳阻力。车辆绕$x$轴做滚动运动；
• $y$轴上的力：转向力、离心力和侧风力。车辆绕$y$轴做俯仰运动；
• $z$轴上的力：地面支持力、风压力。车辆绕$z$轴做横摆运动；

在单车模型假设的前提下，做以下假设：

• 只考虑纯侧偏轮胎特性，忽略轮胎力的横纵向耦合关系；
• 不考虑载荷转移；
• 忽略横纵向空气动力学。
  

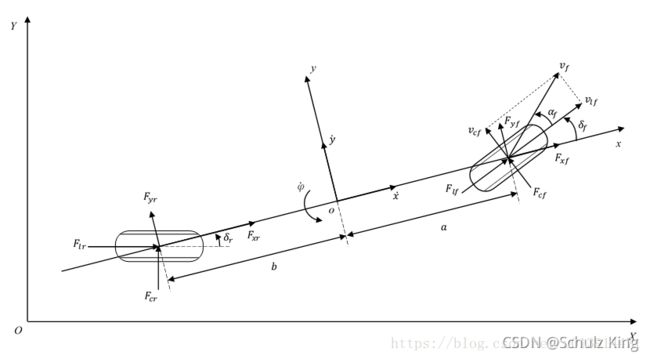
如图所示，单车模型具有两个自由度：绕$z$轴的横摆运动和沿$x$轴的纵向运动。轮胎滑移角是轮胎方向和轮胎速度方向的夹角，产生原因主要是由于轮胎所受合力并非朝向车轮行进的方向，但车轮的偏移角通常较小。

根据牛顿第二定律，分别沿$x$轴、$y$轴、$z$轴做受力分析：

在$x$轴：
$$m{a}_x=F_{x,f}+F_{x,r}\text{\hspace{1em}(1)}$$
在$y$轴：
$$m{a}_y=F_{y,f}+F_{y,r}\text{\hspace{1em}(2)}$$
在$z$轴：
$$I_z\ddot{\psi }=a{F}_{y,f}-b{F}_{y,r}\text{\hspace{1em}(3)}$$

车辆在$y$轴的加速度$a_y$由两部分构成：$y$轴的位移相关的加速度$\ddot{y}$和向心加速度$v_x\dot{\psi }$：
$$a_y=\ddot{y}+v_x\dot{\psi }\text{\hspace{1em}(4)}$$
则公式(2)转变为：
$$m(\ddot{y}+v_x\dot{\psi })=F_{y,f}+F_{y,r}\text{\hspace{1em}(5)}$$
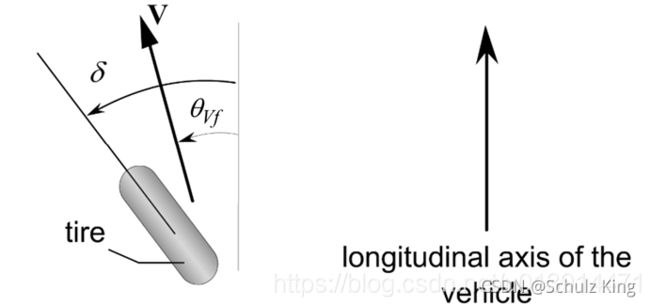
由于轮胎受到横向压力，会有一个很小的滑移角，如下图所示：

前后轮滑移角：
$$\{\begin{array}{l}{\alpha }_f=\delta -{\theta }_{v,f}\\ {\alpha }_r=-{\theta }_{v,r}\end{array}\text{\hspace{1em}(6)}$$
其中，${\theta }_{v,f}$为前轮速度方向，$\delta$为前轮转角，${\theta }_{v,r}$为后轮速度方向，后轮转角为$0$。

前后轮所受横向力为：
$$\{\begin{array}{l}{F}_{y,f}=2C_{\alpha ,f}{\alpha }_f=2C_{\alpha ,f}(\delta -{\theta }_{v,f})\\ F_{y,r}=2C_{\alpha ,r}{\alpha }_r=2C_{\alpha ,r}(-{\theta }_{v,r})\end{array}\text{\hspace{1em}(7)}$$
其中，$C_{\alpha ,f},C_{\alpha ,r}$分别为前后轮胎的侧偏刚度，因为前后各有两个轮胎，因此乘以$2$。

${\theta }_{v,f}，{\theta }_{v,r}$的计算如下：
$$\{\begin{array}{l}\tan ({\theta }_{v,f})=\frac{v_y+l_f\dot{\psi }}{v_x}\\ \tan ({\theta }_{v,r})=\frac{v_y-l_r\dot{\psi }}{v_x}\end{array}\text{\hspace{1em}(8)}$$
根据小角度近似可得：
$$\{\begin{array}{l}{\theta }_{v,f}=\frac{\dot{y}+l_f\dot{\psi }}{v_x}\\ {\theta }_{v,r}=\frac{\dot{y}-l_r\dot{\psi }}{v_x}\end{array}\text{\hspace{1em}(8)}$$
整理可得状态方程：
$$\frac{d}{dt}\left[\begin{array}{c}y\\ \dot{y}\\ \psi \\ \dot{\psi }\end{array}\right]=\left[\begin{array}{cccc}0& 1& 0& 0\\ 0& -\frac{2C_{\alpha ,f}+2C_{\alpha ,r}}{m{v}_x}& 0& -v_x-\frac{2C_{\alpha ,f}{l}_f-2C_{\alpha ,r}{l}_r}{m{v}_x}\\ 0& 0& 0& 1\\ 0& -\frac{2C_{\alpha ,f}{l}_f-2C_{\alpha ,r}{l}_r}{I_z{v}_x}& 0& -\frac{2C_{\alpha ,f}{l}_f^2+2C_{\alpha ,r}{l}_r^2}{I_z{v}_x}\end{array}\right]\left[\begin{array}{c}y\\ \dot{y}\\ \psi \\ \dot{\psi }\end{array}\right]+\left[\begin{array}{c}0\\ \frac{2C_{\alpha ,f}}{m}\\ 0\\ \frac{2l_f{C}_{\alpha ,f}}{I_z}\end{array}\right]\delta \text{\hspace{1em}(9)}$$
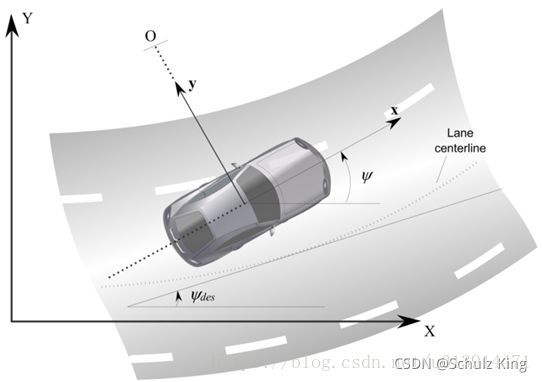
以相对于道路的方向和距离误差为状态变量建立误差动力学模型。假设$e_1$为横向距离误差，车辆质心距离车道中心线的距离，$e_2$为航向误差。

假设车辆的纵向速度为$v_x$，匀速平稳，转向半径为$R$，则车辆转过期望角度所需的角速度为：
$${\dot{\psi }}_{des}=\frac{v_x}{R}\text{\hspace{1em}(10)}$$
所需横向加速度为：
$$a_{y,des}=\frac{v_x^2}{R}=v_x{\dot{\psi }}_{des}\text{\hspace{1em}(11)}$$
则横向加速度误差为：
$${\ddot{e}}_1=a_y-a_{y,des}=(\ddot{y}+v_x\dot{\psi })-v_x{\dot{\psi }}_{des}=\ddot{y}+v_x(\dot{\psi }-{\dot{\psi }}_{des})\text{\hspace{1em}(12)}$$
横向速度误差为：
$${\dot{e}}_1=\dot{y}+v_x(\psi -{\psi }_{des})\text{\hspace{1em}(13)}$$
航向误差：
$$e_2=\psi -{\psi }_{des}\text{\hspace{1em}(14)}$$
可得误差动力学模型为：
$$\frac{d}{dt}\left[\begin{array}{c}{e}_1\\ {\dot{e}}_1\\ e_2\\ {\dot{e}}_2\end{array}\right]=\left[\begin{array}{cccc}0& 1& 0& 0\\ 0& -\frac{2C_{\alpha ,f}+2C_{\alpha ,r}}{m{v}_x}& \frac{2C_{\alpha ,f}+2C_{\alpha ,r}}{m}& \frac{-2C_{\alpha ,f}{l}_f+2C_{\alpha ,r}{l}_r}{m{v}_x}\\ 0& 0& 0& 1\\ 0& -\frac{2C_{\alpha ,f}{l}_f-2C_{\alpha ,r}{l}_r}{I_z{v}_x}& \frac{2C_{\alpha ,f}{l}_f-2C_{\alpha ,r}{l}_r}{I_z}& -\frac{2C_{\alpha ,f}{l}_f^2+2C_{\alpha ,r}{l}_r^2}{I_z{v}_x}\end{array}\right]\left[\begin{array}{c}{e}_1\\ {\dot{e}}_1\\ e_2\\ {\dot{e}}_2\end{array}\right]+\left[\begin{array}{c}0\\ \frac{2C_{\alpha ,f}}{m}\\ 0\\ \frac{2l_f{C}_{\alpha ,f}}{I_z}\end{array}\right]\delta +\left[\begin{array}{c}0\\ \frac{-2C_{\alpha ,f}{l}_f+2C_{\alpha ,r}{l}_r}{m{v}_x}-v_x\\ 0\\ -\frac{2C_{\alpha ,f}{l}_f^2+2C_{\alpha ,r}{l}_r^2}{I_z{v}_x}\end{array}\right]{\dot{\psi }}_{des}\text{\hspace{1em}(15)}$$