点云配准ICP算法推导，SVD分解

前言

最近在看点云配准相关算法，关于点云配准：迭代最近点(Iterative Closest Point, ICP)算法可谓是配准算法的先驱和鼻祖了，该算法于上世纪90年代提出。虽然现在看ICP算法比较老旧，算法精准度也不是很好，但是通过学习ICP的设计原理可以深刻的了解点云配准这个数学问题及纯数学形式的解决思路。
在学习的过程中我发现网上很少有从零基础讲解ICP算法的（可能默认看这类算法的都有很好的数学功底吧），所以我想写一篇关于ICP算法的详细推导博客，希望通过一篇文章帮大家彻底搞懂ICP的原理。后续有可能的话会针对这篇公式推导博客写一篇对应的代码实现博客。
这篇博客适用于点云配准的入门小白，或不多说，上正文！

一、点云配准问题的数学描述

现有两朵点云
$$\mathrm{P}=\left\{{\mathbf{p}}_i\in {\mathbb{R}}^3\mid i=1,\dots ,N\right\}$$
$$\mathrm{Q}=\left\{{\mathbf{q}}_i\in {\mathbb{R}}^3\mid i=1,\dots ,M\right\}$$
需要求解一个刚性变换$\mathrm{T}=R,t$，使得点云$P$和$Q$对齐，（$P$向$Q$对齐），其中$R$是旋转矩阵，$t$是平移向量。找寻刚性变换的过程可以被视做一个最优化的过程（让匹配误差最小，即：该匹配的两个点经过变换后的欧氏距离最小）：

$$\underset{R,t}{\min }\sum _{i=1}^N{\Vert R{p}_i+t-q_i\Vert }^2$$

说明：在真实的点云配准过程中，两朵点云中的数据的数量不一定一致（就是上述定义的M和N），在实际的ICP算法中，算法要先对两朵点云进行关键点匹配，即找到$P$点云中$p_i$点在$Q$点云中的对应点，然后将他们放到对应集合中，找到了上面介绍的一一对应的具有N个点的待配准点云。对应关系寻找的好坏直接决定了算法最后配准的精准度。

二、基于SVD的ICP算法实现步骤

1. 分别求两点云各自的质心：
   $$\bar{p}=\frac{1}{N}\sum _{i=1}^N{p}_i,\cdots \cdot \bar{q}=\frac{1}{N}\sum _{i=1}^N{q}_i$$

2. 对点云坐标去中心化，即：求两点云相对与各自质心的坐标：
   $$x_i=p_i-\bar{p},\cdots \cdots y_i=q_i-\bar{q}$$

3. 利用去中心化后的点云坐标计算$H$矩阵,维数为3*N：
   $$H=\sum _{i=0}^N{x}_i{y}_i^T$$

4. 对$H$矩阵进行SVD分解：
   $$R=U{V}^T$$

5. 验证结果：如果：$det(R)=1$，算法有效；如果：$det(R)=-1$，算法失效

det表示求矩阵的行列式值

7. 计算平移矩阵：
   $$t=Y-X$$

三、ICP算法原理推导

在第一节中介绍：点云配准可以转化为如下数学问题：

$$F(R,t)=\underset{R,t}{\min }\sum _{i=1}^N{\Vert R{p}_i+t-q_i\Vert }^2$$

这是一个二元函数，对于二元函数的求解问题，可以用导数等于0解决。先固定$R$求$t$：
$$\frac{\partial F}{\partial t}=2\sum _{i=0}^{N}t+2R\sum _{i=0}^N{p}_i-2\sum _{i=0}^N{q}_i=0$$
推出：
$$t=\frac{{\sum }_{i=0}^N{q}_i}{{\sum }_{i=0}^{N}1}-\frac{R{\sum }_{i=0}^N{p}_i}{{\sum }_{i=0}^{N}1}=\frac{1}{N}\sum _{i=0}^N{q}_i-R\frac{1}{N}\sum _{i=0}^N{p}_i$$
此时发现公式中出现了去中心化的表达，因此用去中心化的方式表达$t$(算法中的去中心化操作也就是这么来的)：
$$t=\bar{q}-R\bar{p}$$
将$t$带回原始公式$F$中：
$$\begin{gathered} F(R,t)=\underset{R}{\min }\sum _{i=1}^N{\Vert R{p}_i+\bar{q}-R\bar{p}-q_i\Vert }^2 \\ =\underset{R}{\min }\sum _{i=1}^N{\Vert R\left(p_i-\bar{p}\right)-\left(q_i-\bar{q}\right)\Vert }^2 \\ =\underset{R}{\min }\sum _{i=1}^N{\Vert R{x}_i-y_i\Vert }^2 \end{gathered}$$
其中：
$$\begin{array}{rl}{\Vert R{x}_i-y_i\Vert }^2=& {\left(R{x}_i-y_i\right)}^T\left(R{x}_i-y_i\right)=\left(x_i^T{R}^T-y_i^T\right)\left(R{x}_i-y_i\right)\\ & =x_i^T{x}_i-y_i^{T}R{x}_i-x_i^T{R}^T{y}_i+y_i^T{y}_i\end{array}$$
因为$x_i$和$y_i$的维度是1×3，$R$的维度是3×3，因此$y_i^{T}R{x}_i$ 和$x_i^T{R}^T{y}_i$是一个常数，对于一个常数来说，它的转置等于它本身：
$$x_i^T{R}^T{y}_i={\left(x_i^T{R}^T{y}_i\right)}^T=y_i^{T}R{x}_i$$
因此，上面的展开式子可以写成：
$${\left(R{x}_i-y_i\right)}^T\left(R{x}_i-y_i\right)=x_i^T{x}_i-2y_i^{T}R{x}_i+y_i^T{y}_i$$
将展开式代入到F函数中便可得：
$$F(R,t)=\underset{R}{\min }\sum _{i=1}^N\left(x_i^T{x}_i-2y_i^{T}R{x}_i+y_i^T{y}_i\right)$$
观察此时的$F$函数发现，函数中的第一项和第三项没有$R$的作用，都是常数项，对于一个最优化问题来说没有贡献，因此该最优化问题的结果仅由第二项决定：
$$F(R,t)=\underset{R}{\min }\sum _{i=1}^N-2y_i^{T}R{x}_i$$
去掉负号和前面的常系数便可以将最小化问题转化成最大化问题：
$$\underset{R}{\max }\sum _{i=1}^N{y}_i^{T}R{x}_i$$
观察$y_i^{T}R{x}_i$这个式子的特点：

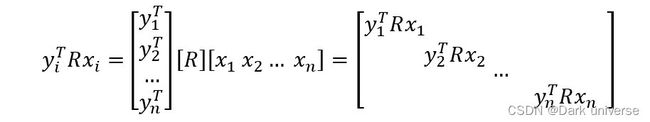
可以发现式子上的数都在这个矩阵的对角线上，这样便可以用矩阵的迹来进行进一步的表示，最大化式子可以表示成：
$$\underset{R}{\max }\sum _{i=1}^N{y}_i^{T}R{x}_i=\max \left(\sum _{i=1}^N\mathrm{trace}\left(y_i^{T}R{x}_i\right)\right)$$
根据矩阵迹的性质$trace(AB)=trace(BA)$对上面的式子进项变换可得：
$$trace(y_i^{T}R{x}_i)=trace(R{x}_i{y}_i^T)$$
记：${\sum }_{i=1}^N{y}_i^T{x}_i$为矩阵$H$(算法中要设置H的原因)，上述的式子便可进一步化简：
$$\begin{array}{rl}\underset{R}{\max }\sum _{i=1}^N{y}_i^{T}R{x}_i=& \underset{R}{\max }\mathrm{trace}\left(R\sum _{i=1}^N\left(x_i{y}_i^T\right)\right)\\ & =\underset{R}{\max }\mathrm{trace}(RH)\end{array}$$
对$H$进行SVD分解:

SVD分解的原理介绍： https://zhuanlan.zhihu.com/p/448767610

$$H=U\Lambda V^T$$
记：
$$L=V{U}^T$$
则：
$$LH=V{U}^{T}U\Lambda V^T=V\Lambda V^T$$
$LH$为正定矩阵，所以:
$$\mathrm{trace}(RH)\le \mathrm{trace}(LH)$$
当$R=L$时,$RH$的值最大.所以$R$的解为:
$$R=L=V{U}^T$$

总结

ICP是非常经典的点云配准算法，其解决配准的方法在数学上也是非常经典的求解最优化问题。通过对ICP算法的推导，我们可以总结：点云配准的过程实际上就是在求解一个3 * 3大小的旋转矩阵R和一个3 * 1大小的平移矩阵t。