机器学习分类常见评价标准
目录
- 1.准确率(Accuracy)
- 2.精确率(Precision)
- 3.召回率(Recall)
- 4.PR曲线与F1值(F1 Score)
- 5.ROC曲线与AUC
评价分类器性能的指标一般是分类准确率(accuracy),但对于二分类问题,其评价指标为精确率(precision)与召回率(recall),除此之外还有F1值(F1 Score)、PR曲线、ROC曲线、AUC等帮助理解的评估标准。
首先了解一下假阴性、假阳性这些基本概念:
TP——True Positive——真阳性——真实标签为真,模型预测也为真
TN——True Negative——真阴性——真实标签为假,预测结果也为假
FP——False Positive——假阳性——真实标签为假,预测结果为真
FN——False Negative——假阴性——真实标签为真,预测结果为假
为了便于理解,你可以把它想象中最近的核酸检测结果,比如你本来没有感染新冠病毒,但核酸检测为阳性,此时就是假阳性(不是真的阳性,即真实标签为假,但预测结果为真)
1.准确率(Accuracy)
A C C = T P + T N T P + T N + F P + F N ACC = \frac{TP+TN}{TP+TN+FP+FN} ACC=TP+TN+FP+FNTP+TN
我们日常生活中都很常用的评价标准,即模型预测正确(包括正例和负例)的数量占所有样本数量之比。准确率看起来非常好理解且直观,但为什么不能只用准确率就判断模型好坏?因为在面对小概率事件时,准确率高不能代表模型性能好。比如最近疫情严峻,如果我们设计了一个模型来预测一位患者是否感染了新冠病毒,分类结果只有是和否。由于我们在抗击疫情中的努力,阳性的病例在人群中肯定是非常少的,所以这个模型只需要预测否,就能达到很高的准确率,如果拿全国的人口作为基数,那准确率高达99%,但实际上这个模型没有任何用处,因为他和直接print("否")没什么区别。
2.精确率(Precision)
P = T P T P + F P P = \frac{TP}{TP+FP} P=TP+FPTP
表示所有被预测为真的例子中实际也为真的概率。在准确率中的例子中,准确率很高的模型精确率却是0,足以看出准确率的问题所在。这个评价标准的意义在于:当模型预测结果为真的时候,我们有多大的把握相信它(在没有真实标签参考的时候)。比如上面的例子,如果模型预测出一个人感染新冠病毒为真,那么我们相信它的底气自然来自与它之前预测阳性的时候对了多少,对的越多那么我们越能相信它。
3.召回率(Recall)
r e c a l l = T P T P + F N recall = \frac{TP}{TP+FN} recall=TP+FNTP
表示所有真实标签为真的例子中模型预测也为真的数量之比。表示模型能从真样本中预测出真的能力。继续以上述例子为证,则召回率意义在于:有N个真的感染新冠病毒的患者,模型能判断出其中的几个,即召回了几个(所以叫召回率)。
精确率:猜的真的样本中,有多少样本确实是真的
召回率:样本是真的中,有多少也被猜是真的
4.PR曲线与F1值(F1 Score)
横坐标为召回率,纵坐标为精确率的坐标系,设置模型预测不同的阈值(比如0.5,大于0.5为正例,小于0.5为负例),其中得到的精确率和召回率即一个PR值,将不同阈值的PR值在上面的坐标系中绘制出来,即为PR曲线。
以下图即说明来源:https://zhuanlan.zhihu.com/p/64963796,讲的很好
P-R曲 线上的一个点代表着,在某一阈值下,模型将大于该阈值的结果判定为正样本, 小于该阈值的结果判定为负样本,此时返回结果对应的召回率和精确率。整条P-R 曲线是通过将阈值从高到低移动而生成的。
上面说的阈值从高到低原因:阈值高,精确率高,阈值低,召回率高
我的理解:阈值高的时候,比如0.9的时候,只有模型预测>0.9的时候才分类为正例,则此时预测正例的数量变少,模型预测正例是真的正例的概率变大,因为此时模型只有90%的把握才会预测为正例,所以精确率很高,但召回率因为真实标签为正的数量没有改变,而TP变少小,所以很小。相反,阈值低的时候,预测正例变多,但预测正例是真实正例的概率变小,精确率也变小,召回率变大。
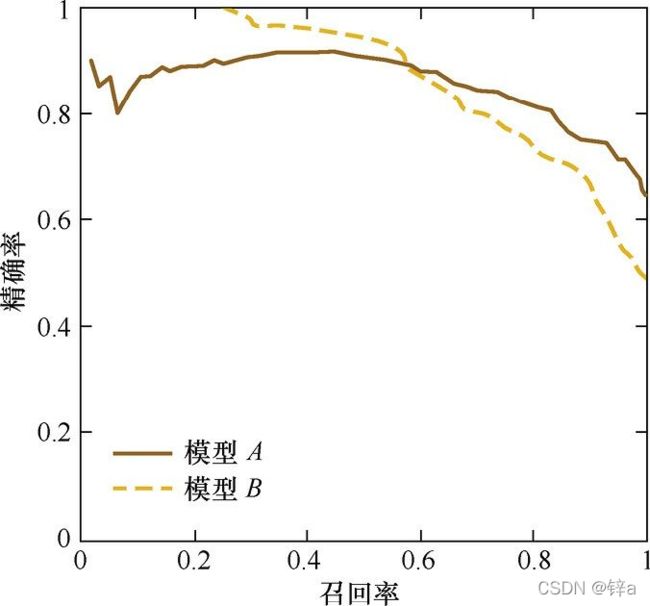
由图可见,当召回率接近于0时,模型A的精确率为0.9,模型B的精确率是1, 这说明模型B得分前几位的样本全部是真正的正样本,而模型A即使得分最高的几 个样本也存在预测错误的情况(也就是说模型A在有9成把握预测为正的时候还是犯错了)。并且,随着召回率的增加,精确率整体呈下降趋 势。但是,当召回率为1时,模型A的精确率反而超过了模型B(这说明模型B对一些真实标签为正例的预测把握极低,比如一个标签为正例的样本,模型B可能只将其预测为0.1)。这充分说明,只用 某个点对应的精确率和召回率是不能全面地衡量模型的性能,只有通过P-R曲线的 整体表现,才能够对模型进行更为全面的评估。
当一个模型的PR曲线完全盖住了另一个模型,那么前者肯定是更优秀的模型,因为它所有点的精确率和召回率都优于后者。那么如果向上图那样两个模型互有交叉,无法直观判断模型的好坏,就需要通过其他方法:比较PR曲线下的面积,或者比较平衡点(坐标系上画一条召回率=精确率的直线,即过原点斜率为1,直线与PR曲线的交点就是平衡点)
但平衡点往往过于简单,一般考察两个模型的F1值,即精确率与召回率的调和平均:
F 1 = 2 1 r e c a l l + 1 p r e i s i o n = 2 × r e c a l l × p r e c i s i o n r e c a l l + p r e c i s i o n F1 = \frac{2}{\frac{1}{recall}+\frac{1}{preision}}=\frac{2\times recall\times precision}{recall+precision} F1=recall1+preision12=recall+precision2×recall×precision
5.ROC曲线与AUC
与PR曲线不同,ROC曲线的横坐标是真正例率(TPR,其实就是召回率,所有正例中猜对的),纵坐标为假正例率(FPR,所有负例中猜错的)。
T P R = T P T P + F N F P R = F P T N + F P TPR = \frac{TP}{TP+FN}\\ FPR = \frac{FP}{TN+FP} TPR=TP+FNTPFPR=TN+FPFP
ROC曲线将模型预测得分进行排名,分别取得分为阈值进行计算TPR和FPR,最后进行绘制,以下是举例:
| 序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| 预测值 | 0.9 | 0.8 | 0.7 | 0.6 | 0.5 | 0.4 | 0.3 | 0.2 | 0.15 | 0.1 |
| 真实标签 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 1 | 0 |
- 先以第一个样本的得分作为阈值,即模型大于该阈值分类为1,反之为0。此时预测为正的有1个样本,真实标签为1的有6个样本,分类正确的有1个样本,即TP = 1,FP = 0,TPR = 1/6,FPR = 0
- 以第二个样本的得分作为阈值,此时TP = 2,FP=0,TPR = 2/6,FPR = 0。以此类推:
- TP = 2,FP = 1,TPR = 2/6,FPR = 1/4
- TP = 3,FP = 1,TPR = 3/6,FPR = 1/4
- TP = 4,FP = 1,TPR = 4/6,FPR = 1/4
- TP = 5,FP = 1,TPR = 5/6,FPR = 1/4
- TP = 5,FP = 2,TPR = 5/6,FPR = 2/4
- TP = 5,FP = 3,TPR = 5/6,FPR = 3/4
- TP = 6,FP = 3,TPR = 6/6,FPR = 3/4
- TP = 6,FP = 3,TPR = 6/6,FPR = 4/4
绘制成图:
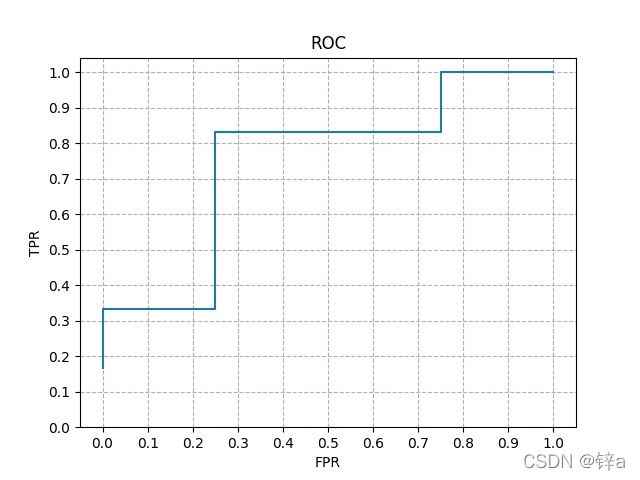
如果两个模型PR曲线相似,一个模型的ROC曲线被另一个模型完全覆盖,则后者的性能优于前者,如果两个模型ROC曲线交叉,则难以分辨孰优孰劣,此时可以分析ROC曲线下的面积:
AUC即(Area Under ROC Curve),是ROC曲线下各部分的面积求和而得。AUC越大,则代表模型预测能力越强。