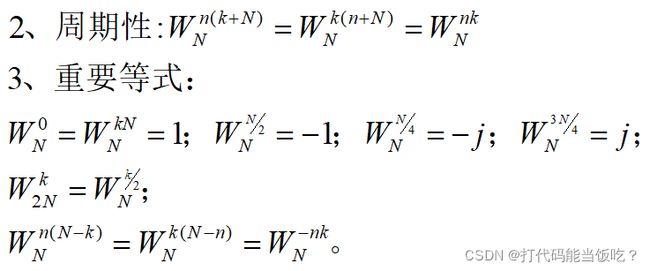数字图像处理(冈萨雷斯版)期末总复习
- 第一章 绪论
-
-
- 什么叫图像?什么叫数字图像?什么叫像素?
- 什么叫数字图像处理?
- 数字图像的数学本质?数字图像的物理本质?
- 灰度图像和彩色图像的存储量计算方法?
- 彩色图像转灰度图像的方法?
- 简述采样定理
-
- 第二章 灰度变换与空间滤波
-
-
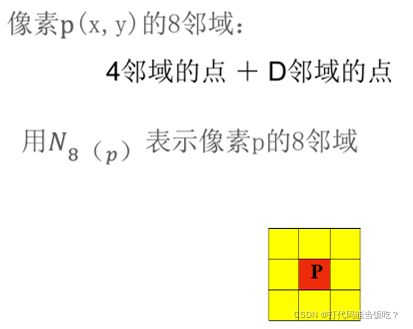
- 叙述图像邻域的概念
- 具有什么性质的函数才能成为亮度变换函数
- 归一化直方图
- 直方图均衡化
- 直方图规定化
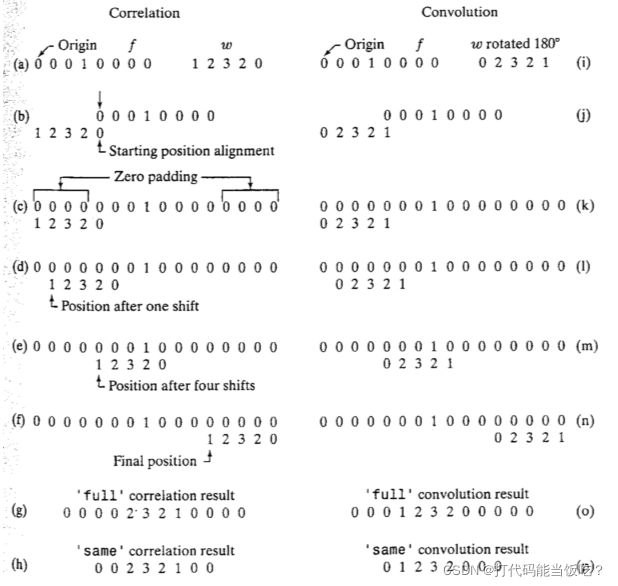
- 相关和卷积
- 空间滤波
-
- 第三章 频域变换
-
-
- 傅里叶变换定义式
- 傅里叶变换旋转因子性质
- 傅里叶变换及逆变换
-
- 第四章 图像压缩
-
-
- 信息熵,平均码长,冗余度,编码效率的定义
- Huffman编码的基本原理是什么?如何求解Huffman编码?
- 算术编码的基本原理是什么
- 行程编码的基本原理是什么?如何求解形成编码
-
- 第五章 图像分割
-
-
- 梯度算子的基本原理及其优缺点?
- Roberts算子的基本原理及其优缺点?
- Prewitt和Sobel算子的基本原理及其优缺点?
- Laplacian算子的基本原理及其优缺点?
- Marr算子的基本原理及其优缺点?
- Hough变换线检测的基本原理及计算步骤
-
第一章 绪论
什么叫图像?什么叫数字图像?什么叫像素?
图像是指景物在某种介质上再现的视觉信息。图像是具有特定信息的某种集合体,本质上图像可以认为是数据的集合。
一幅图像可以定义为一个二维函数f(x,y),其中x,y是空间坐标,而f在任意坐标(x,y)处的幅度称为图像在该点的灰度或亮度。当x,y,f的幅值都是有限的离散值时,称该图像为数字图像。简单的说:数字图像是指可用矩阵或者数组表示的图像。
像素是指在由一个数字序列表示的图像中的一个最小单位。
什么叫数字图像处理?
数字图像处理领域就是借助计算机来处理数字图像(通过计算机对图像进行去除噪声,增强,复原,分割,提取特征等处理的方法和技术)。包括从图像到图像的低级处理,从图像中提取特征的中级处理,从图像中识别目标的高级处理。
数字图像的数学本质?数字图像的物理本质?
数学本质:一幅图像可以被定义为一个二维函数f(x,y),其中:x,y是平面坐标,f是x,y处的振幅,称为该点的亮度或灰度。
物理本质:一种辐射能量的空间分布T(x,y,z,t,γ),其中x,y,z是空间变量,t代表时间变量,γ是频谱变量(波长)。
灰度图像和彩色图像的存储量计算方法?
灰度图像 = 长度方向像元素 * 宽度方向像元素 * 1(Bytes)
彩色图像 = 长度方向像元素 * 宽度方向像元素 * 3(Bytes)
彩色图像转灰度图像的方法?
1.浮点运算:Gray = R * 0.3 + G * 0.59 + B * 0.11
2.整数方法:Gray = (R * 30 + G * 59 + B * 11) / 100
3.移位方法:Gray = (R * 76 + G * 151 + B * 28) >> 8
4.平均值法:Gray = (R + G + B) / 3
5.仅取绿色:Gray = G
简述采样定理
采样定理,又称香农采样定理,奈圭斯特采样定理:对一个频率在0~fc内的连续信号进行采样,当采样频率为fs≥2fc时,由采样信号xs(nTs)能无失真地回复为原来信号x(t)。
第二章 灰度变换与空间滤波
叙述图像邻域的概念
具有什么性质的函数才能成为亮度变换函数
由于亮度变换仅取决于亮度的值,而与位置(x,y)无关,故亮度变换函数通常可写作如下公式:

1.变换函数必须是单调函数
2.变换函数不必严格单调
3.可以是分段函数
4.可线性变换也可非线性变换
5.参数的自适应至今依然是个问题
归一化直方图
图像归一化是指对图像进行了一系列标准的处理变换,使之变换为一固定标准形式的过程,该标准图像成为归一化图像。直方图归一化的本质就是让变化后的直方图每一个像素等级的概率相等

根据归一化函数绘制归一化直方图:
f=imread('1.jpg');
g=rgb2gray(f);
[rows,clos]=size(g);
[counts,xs]=imhist(g);
counts = counts/(rows*clos)
bar(xs,counts);
直方图均衡化
通过改变图像的直方图来改变图像中像素的灰度,主要用于增强动态范围偏小的图像对比度
直方图均衡化计算过程:
1.计算累计直方图概率sk。
2.根据公式int((灰度级数-1)*sk+0.5)对累计直方图概率进行取整数
3.根据原灰度级与第二步取整的结果找出他们的对应关系(即让灰度级与相同的取整的结果对应)
4.根据映射结果列出新的直方图分布概率
直方图规定化
所谓直方图规定化就是通过一个灰度映像函数,将原灰度直方图改造成所希望的直方图。
直方图规定化计算过程:
1.计算累计直方图概率sk。
2.计算规定模板的直方图概率s’k
3.SML映射(找到与各个sk相近的s’k。
4.根据映射结果列出新的直方图分布概率
相关和卷积
空间滤波
空间滤波(spatial filtering),也称邻域处理(neighbour processing ),主要包括以下步骤:
1、定义中心点(x,y);
2、仅对以(x,y)为中心点的邻域内的像素进行运算;
3、令运算结果为该点的处理响应;
4、对图像中的每一点重复此步骤。
若对邻域内像元的计算为线性运算时,则称线性空间滤波
若对邻域内像元的计算为非线性运算时,则称非线性空间滤波
第三章 频域变换
傅里叶变换定义式
可以将傅里叶变换比作一个玻璃棱镜。棱镜是可以将光分解为不同颜色的物理仪器,每个成分的颜色由波长(或频率)来决定。傅里叶变换可以看作是数学上的棱镜,将函数基于频率分解为不同的成分。当我们考虑光时,讨论它 的光谱或频率谱。同样,傅立叶变换使我们能通过频率成分来分析一个函数。

傅里叶变换旋转因子性质
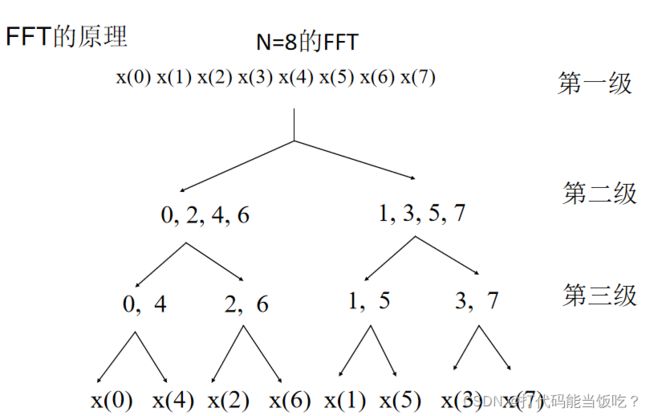
傅里叶变换及逆变换
N=8的FFT
1.把一个序列分为长度减半的偶序列和奇序列, 原序列的DFT就由这两个N/2序列求得。
2.进一步把N/2序列分解成两个N/4序列, 一直分解到单点序列。
以L=3, N=8为例,需要三级分解。

离散傅里叶逆变换(IDFT)

定义法计算IDFT的过程:
1.把DFT中的每一个系数中的nk改为-nk
2.再乘以常数 1/N
第四章 图像压缩
信息熵,平均码长,冗余度,编码效率的定义
平均码长:

冗余度:通俗的讲就是数据的重复度,在数据集合中重复的数据称为数据冗余。


编码效率:

Huffman编码的基本原理是什么?如何求解Huffman编码?
基本思想:频率高的,赋给短码;频率低的,赋给长码。
Huffman编码求解过程:
1.将信号源wi的概率从大到小纵向排列
2.将概率最小的两个wi(排序完后都是最后两个)相加然后再形成新的一列wi,再继续从大到小排序,直至最后两个wi的和为1.0
3.根据上0下1的编码格式,从概率最低的开始从左往右编码。
4.把编码结果倒置就形成了Huffman编码。
算术编码的基本原理是什么
基本原理:将待压缩的整段数据映射到实数半开区间[0,1)内,以某一区段的任一个数值作为数据段的唯一可译代码。
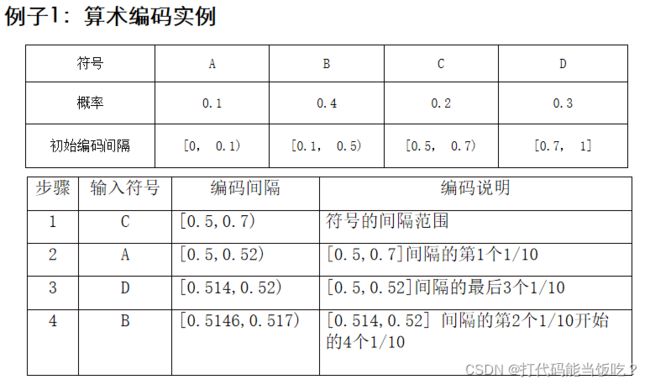
行程编码的基本原理是什么?如何求解形成编码
基本原理:在给定的图像数据中寻找连续重复的数值,然后用两个字符值取代这些连续值。
例子:
计算 aabbbbbbcccccdeee 的行程编码 。
解答:2a6b5c1d3e
第五章 图像分割
梯度算子的基本原理及其优缺点?
Roberts算子的基本原理及其优缺点?
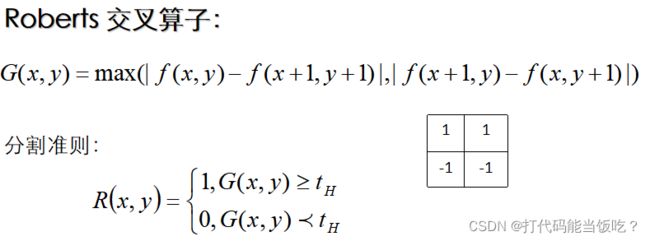
Roberts算子利用局部差分算子寻找边缘,不具备抑制噪声的能力,但对具有陡峭边缘噪声少的图像效果较好,尤其是边缘±45°较多的图像,但定位准确率较差,提取边缘线条较粗。
Prewitt和Sobel算子的基本原理及其优缺点?

Prewitt算子对灰度渐变的图像边缘提取效果较好,而没有考虑相邻点的距离远近对当前像素点的影响,与Sobel算子类似,不同是在平滑部分的权重大小有差异
Sobel算子考虑了综合因素,对噪声较多的图像处理效果更好,边缘定位效果不错,但检测出的边缘容易出现多像素宽度。
Laplacian算子的基本原理及其优缺点?

Laplacian 算子不依赖于边缘方向的二阶微分算子,对图像中的阶跃型边缘点定位准确,该算子对噪声非常敏感,它使噪声成分得到加强,这两个特性使得该算子容易丢失一部分边缘的方向信息,造成一些不连续的检测边缘,同时抗噪声能力比较差,由于其算法可能会出现双像素边界,常用来判断边缘像素位于图像的明区或暗区,很少用于边缘检测;
Marr算子的基本原理及其优缺点?
Hough变换线检测的基本原理及计算步骤
基本原理:


计算步骤:
1. 适当地离散化参数空间.
2. 为参数空间的每一个单元设置一个累加器,
3. 把累加器初始化为零.
4. 对图像空间的每一点,在其所满足的参数方 程对应的累加 器上加1.
5. 累加器阵列的最大值对应模型的参数.