nms和softnms的代码

前言

nms和softnms的原理及相关简单代码总结

预测框筛选的方法

预测框的筛选，是检测模块后处理阶段的一个十分重要的过程。因为我们预测输出的预测框，几乎大部分都不是一一对应的（DETR里的是一一对应的），所以一个目标我们可能预测许多框，这些框的分类分数和位置都不同，进行验证和 推理的时候，我们就要使用相应的方法去进行我们预测框的筛选。

1.nms

nms:非极大值抑制。

1> 根据检测框的分类分数（置信度得分）进行降序排序，选取同类分数最高的检测框；
2> 分别计算检测框与相邻检测框的重叠度IOU，对大于阈值Nt的检测框得分直接置零，也就是舍去,并标记将检测框保留下来；
3> 重复这个过程，找到所有被保留下来的检测框；

把iou值大于所给的阈值的框给置为0筛选掉
这里提供cpu版本的简单的nms实现，现在pytorch里提供的都是使用GPU的nms算子，速度要快的多

import numpy as np
import matplotlib.pyplot as plt

def nms_cpu(dets,iou_thres):
    # 计算交集和并集，准备计算IOU
    x1 = dets[:,0]   # 二维的变成一维的了
    y1 = dets[:,1]
    x2 = dets[:,2]
    y2 = dets[:,3]
    scores = dets[:,4] 

    areas = (x2-x1+1)*(y2-y1+1)  # +1 是为了避免一些小数计算
    # print(areas) 
    keep = [] # 定义一个列表，用来存放NMS后剩余的方框  
    index = scores.argsort()[::-1] # 取出分数从大到小排列的索引    
    # index
    while index.size>0:
        # 取出第一个方框和其他方框进行比对，看又没有
        i = index[0]
        keep.append(i) # keep先保留的是索引值，不是具体的分数
        
        # IOU计算
        x_l = np.maximum(x1[i],x1[index[1:]])   # 会减少一个框坐标
        y_l = np.maximum(y1[i], y1[index[1:]])  # 当index只有一个值的时候，order[1]会报错说index out of range，而index[1:]会是[]，不报错
        x_r = np.minimum(x2[i],x2[index[1:]])
        y_r = np.maximum(y2[i], y2[index[1:]])
        # 注意，如果两个方框相交，计算为正，不相交计算为负,负的设置为0
        h = np.maximum(0,y_r-y_l+1)
        w = np.maximum(0,x_r-x_l+1)       
        # 计算交集
        intersection = h*w
        union = areas[i]+areas[index[1:]]-intersection
        ious = intersection/union+1e-8   # 1e-8考虑分母可能为0的情况     
        # 使用iou阈值，把iou值大于所给的阈值的框给筛选掉
        idx = np.where(ious<=iou_thres)[0]  # 只有条件 (condition)，没有x和y，则输出满足条件 (即非0) 元素的坐标,
        # 把留下的框再次进行NMS操作     # 坐标以tuple的形式给出,通常原数组有多少维，输出的tuple中就包含几个数组，分别对应符合条件元素的各维坐标。
        index = index[idx + 1]
    return keep

画图，可视化下看看：
参考：https://blog.csdn.net/EMIvv/article/details/122484524

# 画图展示过程
def draw_boxes(boxes,color):
    x1 = boxes[:,0]   # 二维的变成一维的了
    y1 = boxes[:,1]
    x2 = boxes[:,2]
    y2 = boxes[:,3]
    s = boxes[:,4]
    print(s)
    plt.plot([x1,x1],[y1,y2],color)
    plt.plot([x1,x2],[y1,y1],color)
    plt.plot([x1,x2],[y2,y2],color)
    plt.plot([x2,x2],[y1,y2],color)
    for i in range(len(s)):
        plt.text(float(x1[i]), float(y2[i]), str(round(s[i],3)),ha='center', fontdict=None,bbox=dict(facecolor='red', alpha=0.5))

boxes = np.array([[100, 100, 210, 210, 0.72],
                  [250, 250, 420, 420, 0.8],
                  [220, 220, 320, 330, 0.92],
                  [200, 210, 300, 300, 0.81],
                  [220, 230, 315, 340, 0.9]])

keep = nms_cpu(boxes,0.6)
plt.figure()
ax1 = plt.subplot(121)
ax2 = plt.subplot(122)
plt.sca(ax1)
draw_boxes(boxes,'b')
plt.sca(ax2)
draw_boxes(boxes[keep],'r')
plt.show()

2.softnms

softnms:是对nms的重叠框处理的方法的改进，认为直接舍去可能不太好，有可能存在同一类的两个目标靠的比较近的情况。所以提出用温和的手段去处理重叠的框，给重叠的框乘以一个与Iou值有关的因子，来控制iou大的分类分数。与nms不同的是，最后是根据所给的分数阈值取框，而不是iou阈值。

1> 根据检测框的置信度得分进行降序排序，选取分数最高的检测框A，
2> 分别计算检测框与相邻检测框的重叠度IOU，对大于阈值的检测框设置一个惩罚函数，降低这些检测框的置信度得分
3> 重复这个过程，找到所有被保留下来的检测框

• 1.线性因子，大于阈值的部分乘以（1-iou）:这样重叠度高的，si会变小，比如最大的分类分数为0.9，iou=0.7大于阈值的一个框si=0.6,这样0.6*（1-0.7）=0.18，这样一下降低了分数，后续要根据重新计算的分数阈值筛选。
  
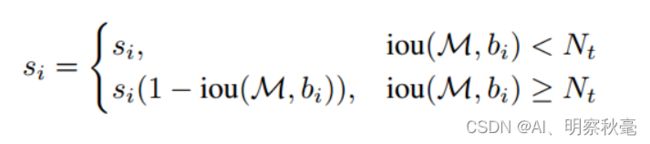
• 2.高斯置信度降低策略，所有原来的分数乘以一个与iou有关的高斯变量。因为高斯变量符合均值为0，所以这样没有重叠的分类分数还是si，重叠的iou值越大，相乘后分数越低。但是没线性一下降低这么多，相对来说更加平缓。
  

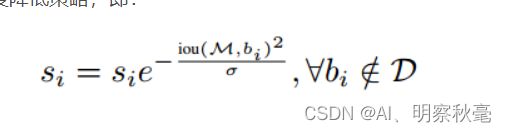
def softnms_cpu(dets,iou_thres,score_thres,sigma=0.5,method=1):
    # 计算交集和并集，准备计算IOU
    x1 = dets[:,0]   # 二维的变成一维的了
    y1 = dets[:,1]
    x2 = dets[:,2]
    y2 = dets[:,3]
    scores = dets[:,4] # 没有新开辟
    areas = (x2-x1+1)*(y2-y1+1)  # +1 是为了避免一些小数计算
    # print(areas) 
    keep = [] # 定义一个列表，用来存放NMS后剩余的方框  
    index = scores.argsort()[::-1] # 取出分数从大到小排列的索引 
    # index
    while index.size>0:
        # 取出第一个方框和其他方框进行比对，看又没有
        i = index[0]
        keep.append(i) # keep先保留的是索引值，不是具体的分数
        
        # IOU计算
        x_l = np.maximum(x1[i],x1[index[1:]])   # 会减少一个框坐标
        y_l = np.maximum(y1[i], y1[index[1:]])  # 当order只有一个值的时候，order[1]会报错说index out of range，而order[1:]会是[]，不报错
        x_r = np.minimum(x2[i],x2[index[1:]])
        y_r = np.maximum(y2[i], y2[index[1:]])
        # 注意，如果两个方框相交，计算为正，不相交计算为负,负的设置为0
        h = np.maximum(0,y_r-y_l+1)
        w = np.maximum(0,x_r-x_l+1)
        
        # 计算交集
        intersection = h*w
        union = areas[i]+areas[index[1:]]-intersection
        ious = intersection/union+1e-8   # 1e-8考虑分母可能为0的情况
        
        # 不同的地方
        if method==0:  # 线性惩罚
            weights = np.ones(ious.shape)
            weights[ious>=iou_thres] = weights[ious>=iou_thres]-ious[ious>=iou_thres] 
        elif method==1:
            weights = np.exp(-ious*ious/sigma)
            
        # 更新分数
        scores[index[1:]] *= weights
        # 更新索引
        update_index = scores[index[1:]].argsort()[::-1]+ 1 # 因为是在index里排序，所以后面再取索引时，到原来的index里取就行了
        print(update_index)
        index = index[update_index]   # 取索引时，到原来的index里取
        # 这里不同的是用置信度分数作为筛选的依据了
        keep_idx = np.where(scores[index]>score_thres)[0]
        index = index[keep_idx]
    return keep

画图：

def draw_boxes(boxes,color):
    x1 = boxes[:,0]   # 二维的变成一维的了
    y1 = boxes[:,1]
    x2 = boxes[:,2]
    y2 = boxes[:,3]
    s = boxes[:,4]
    print(s)
    plt.plot([x1,x1],[y1,y2],color)
    plt.plot([x1,x2],[y1,y1],color)
    plt.plot([x1,x2],[y2,y2],color)
    plt.plot([x2,x2],[y1,y2],color)
    for i in range(len(s)):
        plt.text(float(x1[i]), float(y2[i]), str(round(s[i],3)),ha='center', fontdict=None,bbox=dict(facecolor='red', alpha=0.5))

# !!! 这样输入boxes会在函数里改变里面scores的值，返回后一样改变了值，列表是可变的
#keep_sf = softnms_cpu(boxes,iou_thres=0.5,score_thres=0.3,sigma=0.5,method=1)
box1 = boxes.copy()
keep_sf = softnms_cpu(box1,iou_thres=0.5,score_thres=0.1,sigma=0.5,method=1)
# 画图
plt.figure()
ax1 = plt.subplot(121)
ax2 = plt.subplot(122)
plt.sca(ax1)
draw_boxes(box1,'b')   # box1->boxes...box1:表示经过softnms后的
plt.sca(ax2)
draw_boxes(box1[keep_sf],'r')
plt.show()

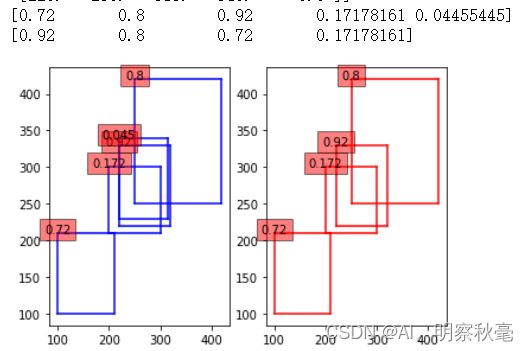
高斯方法的图

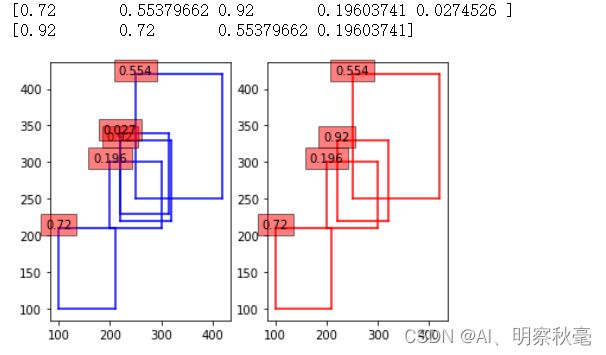
实际上是返回索引，然后在原来的boxes里取相应的框和分数，这里是为了看看softnms后的分数变化。实际上还是下图：只有目标比较密集的时候效果才比较明显，常用的是高斯方法的softnms。而且由上面的图可知用softnms时，分数阈值可以设置的小点。

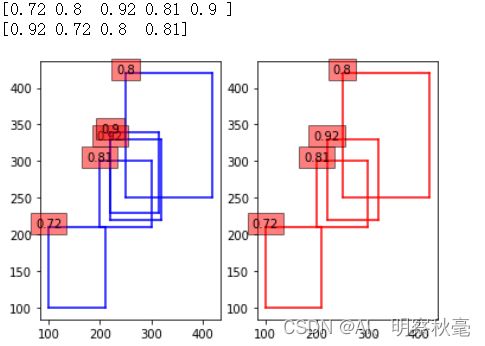
线性方法的图

总结

softnms相对于nms的改进，其实就是一种对原来部分加权进行一种软处理的一种方法，这种方法的思想其实在很多论文里的创新点都有看到过类似的身影。