【机器学习】线性回归之预测商品的销售额
目录
情境:
一、读取数据
二、分析数据
1、热度图 heatmap()
2、散点图
三、特征集和标签集
1、学会查看数据
2、拆分训练集和测试集
四、线性回归
五、开始预测
六、评价测度
七、模拟效果对比图 ROC曲线
八、给模型打分
情境:
一家商店为了扩大销售额,进行了宣传
采用了以下三种方式:
微信:wechat
报纸:newspaper
电视:tv
而销售额:sales(千元)
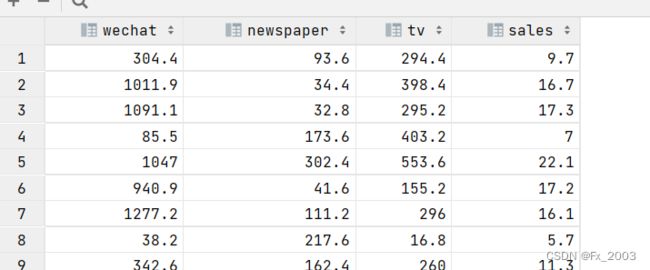
一、读取数据
数据的读取 pandas 的 read_csv
nidm 阶
shape (200,4)两百行4列
head()前五条数据
tail()后五条数据
import pandas as pd
data = pd.read_csv('./data/advertising.csv')
print(data.ndim) # 维度(阶
print(data.shape) # (200,4) 说明有两百条数据,4列 其中第四列sales作为标签 ,其他三个为特征
data.head() # 显示前五条数据二、分析数据
1、热度图 heatmap()
# 分析数据
# 可视化数据
# 数据的相关分析
# seaborn 包,这个包数据可视化效果比较好,其实它也属于Matplotlib的内部包,但是需要单独安装
有关seaborn包:
Seaborn的简述_熊️兔的博客-CSDN博客_seaborn
Seaborn详细教程-数据分析必备手册(2万字总结)seaborn中文手册
import matplotlib.pyplot as plt
import seaborn as sns
# sns.heatmap() 热度图
# cmap:设置颜色带的色系
# annot:是否显示数值注释
sns.heatmap(data.corr(),annot=True,cmap='RdBu_r') # 使用data.corr()计算相关系数
plt.show()
# 相关性越高,颜色越深
可以看出,微信宣传效果比较好
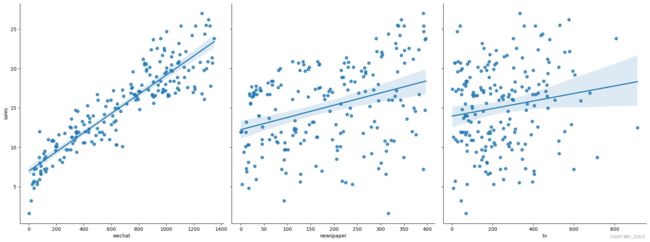
2、散点图
#显示销量和各种广告投放量的散点图
# 参数size,aspect 来调节显示的大小和比例
# kind = 'reg',可以添加一条最佳拟合直线和95%的置信带
sns.pairplot(data,
x_vars=['wechat', 'newspaper', 'tv'],
y_vars='sales',
size=7, aspect=0.9,kind='reg')
plt.show()
# 根据结果可以看出wechat 线性关系比较强可以看到,wechat的拟合线性比较好
三、特征集和标签集
1、学会查看数据
from IPython.core.display_functions import display
# 线性回归模型
'''
优点:快速并且没有调节参数
缺点:相比其他复杂点的模型,它的预测准确率不高,而且它假设特征和标签之间有线性关系,对一些非线性的关系,不能很好进行数据建模
'''
# drop 默认删除行,删除列的话加上 “axis=1”
X = data.drop('sales',axis=1) # 去掉最后一列标签
print('特征集前五条数据\n',X.head())
y = data['sales'] # 从Dataframe 中选择一个Series
display('标签集前五条',y.head())2、拆分训练集和测试集
这里用了sklearn的拆分工具
from sklearn.model_selection import train_test_split
# 构建训练集和测试集
X_train,X_test,y_train,y_test = train_test_split(X,y,random_state=1,train_size=0.7) # train 0.7,test 0.3
# print(X_train.shape) # (140,3)
# print(X_test.shape) # (60, 3)
display(X_train)四、线性回归
# sklearn 的线性回归
from sklearn.linear_model import LinearRegression
linreg = LinearRegression()
model = linreg.fit(X_train,y_train)
print("模型:",model)
print(linreg.coef_) # w
print(linreg.intercept_) # b输出:
模型: LinearRegression()
[0.01170566 0.01323019 0.00058797]
4.599516690419023
五、开始预测
# 预测
y_pred = linreg.predict(X_test)
display(y_pred)六、评价测度
1、线性回归常用的三种:
- 平均绝对误差(MAE)
- 均方误差(MSE)
- 均方根误差(RMSE)
# RMSE
from sklearn import metrics
import numpy as np
sum = 0
for i in range(len(y_pred)):
sum += (y_pred[i] - y_test.values[i]) **2
sum_erro = np.sqrt(sum / len(y_test))
print(sum_erro)
# 上面的代码可以直接这样:
print(np.sqrt(metrics.mean_squared_error(y_test, y_pred)))输出:
1.523063932837681
1.523063932837681
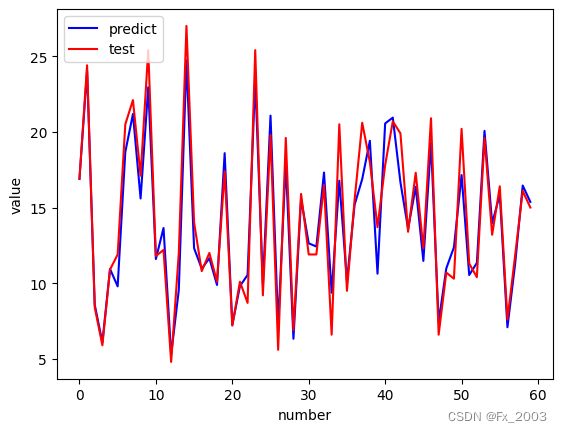
七、模拟效果对比图 ROC曲线
有关ROS曲线:机器学习之ROC曲线_荒野雄兵的博客-CSDN博客_机器学习roc曲线
plt.figure()
plt.plot(range(len(y_pred)), y_pred, 'b', label="predict")
plt.plot(range(len(y_pred)), y_test, 'r', label="test")
# 'upper right', 'upper left',
# 'lower left', 'lower right', 'right',
# 'center left', 'center right', 'lower center',
# 'upper center', 'center'
plt.legend(loc="upper left") # 显示图中的标签 -->左上角
plt.xlabel("number")
plt.ylabel('value')
plt.show()八、给模型打分
linreg.score(X_test, y_test)可以看到还不错