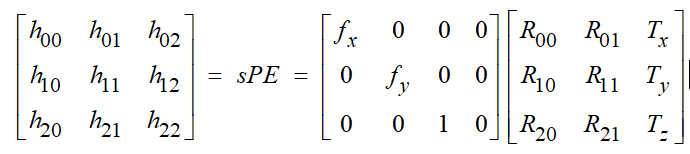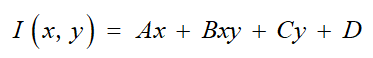Apriltag定位原理与测试

Apriltag定位原理

二维码的检测工作的思路是提取一块四边形的区域，这个区域具有比周围亮度更低的特点。这个思路的主要优点是尽可能多的检测出所有可能的二维码，但是极有可能出现 false positive，后续的编码可以对野值进行剔除。

图 1 二维码检测步骤示意

1.线段的检测

与其他的二维码检测程序相似，首先会计算整个图像上每个像素上的梯度的强度和方向，然后对梯度的强度和方向进行聚类。

聚类算法是基于图的算法：图的节点为图像上每一个像素，图像上相邻的两个像素都存在一条边，边的权值为梯度方向之差。根据边的权值对所有的边进行增序排列，最后会根据边的权值做边的合并。给定一个合并完成边的集合n，边的梯度方向最大值与最小值之差是 D(n)，梯度强度最大值与最小值之差是 M(n)，D(n) 必须在 0 ∼ 2π 之间，所以要对 D(n)做取余的处理。给定两个边集合n和m，当它们满足以下条件，合并这两组边为一组边：

式中： KD和KM ———常量参数，这里取KD = 100 和KM= 1200；

| · |———某一边集合中包含边的数量。

上式约束了两个集合在合并前合的梯度方向接近，KD和KM保证在集合元素数量较少的情况下，能够合并，当合并集合边的数量增大时，边的合并条件会变得更加严苛。由于基于梯度的聚类方法对噪声十分敏感，即使很小的噪声也会造成梯度方向很大的变化。一个好的解决方法就是使用低通滤波器，由于二维码的特征比较大，所以即使低通滤波器会滤掉图像中部分有意义的信息，也不会对最后二维码的检测造成过多的信息丢失。

完成了图像中所有点的聚类，就可以使用加权最小二乘法来拟合直线的方程，每一点的权值就是该点的梯度的强度。通过直线的拟合，得到有向线段的两个端点的坐标p1和 p2，有向线段 p1 p2 的方向为线段p1 p2 的左侧亮度比右侧低。

线段的检测算法在整个二维码提取的流程中所占的时间最多，为了提高检测速度，一般将图像先进性降采样处理，这样能够将速度提高4倍，降采样的过程可以和低通滤波过程一起进行，这样做的一个缺点是会降低图像分辨率，使部分信息丢失，最后导致较小的二维码无法被检测出来。

2.四边形的检测

检测得到所有的线段后，下一步需要挑选线段，对线段分组，每一组线段都是能够构成四边形的候选者。分组遵循以下规则：前一条边的末端点应该和下一条边的始端点之间的距离小于一个阈值，并且相接的线段要构成逆时针的方向。

分组成功后，所有的线段会构成一个树，该树的第一层为所有的有向线段，第二层到最后一层的节点为同一组候选者线段，应用深度优先搜索遍历整个树，若在树的深度为 4 的时候，最后一条边与第一条边构成一个闭环，则说明它们是符合二维码四边形的要求，遍历到该闭环节点的路径就构成了该四边形。

3.单应矩阵和相机外参的估计

定义单应矩阵为从二维码坐标系中的四个角点的齐次坐标到图像二维码四个角点坐标的映射H，单应矩阵可以通过直接线性变换（DLT，Direct Linear Transform）得到。

二维码的位置和姿态的计算需要额外的信息：相机的焦距和二维码的物理距离。3×3 的单应矩阵可以写成3×4的相机内参矩阵P和4×3的外参矩阵E的积。外参矩阵通常是4×4的，但是在二维码坐标系中的四个角点的坐标在z方向为0，所以就可以移除外参矩阵的第三列元素，使用旋转参数Rij和平移参数Tk来表示截取后的外参矩阵，那么单应矩阵就可以表示为：

由于单应矩阵是两组齐次坐标的映射关系，所以存在一个尺度参数s。将上式展开，得到：

由于旋转矩阵为单位正交矩阵，矩阵中列向量的模为1，利用该约束能够计算得到s。我们计算R矩阵中两个列向量的模长均值，得到s的大小，s的符号必须满足二维码在相机坐标系的前向，也就是s要保证 Tz符号为负。通过 DLT 得到的旋转矩阵不一定具有单位正交的特性，所以最后要对R矩阵做极分解。

4.二维码的解码

在二维码的解码过程中，首先将二维码中每一块的坐标通过单应性矩阵映射到图像平面，判断图像平面上映射后的点的像素值是否大于某一个阈值，若大于该阈值，二维码这个坐标上为1，相反，小于该阈值则判定为0。阈值的选取为了满足光照不变性，定义了以下的阈值模型：

该阈值的模型随着图像上坐标的变化而不同，所以能够对不同的光照强度有很强的鲁棒性。

上式具有4个参数，我们使用二维码的边界上的点来训练该模型，因为二维码边界上的像素值都是已知的，一种为高亮度区域，另外一种为暗色区域。分别对这两种区域建立两个模型，对模型进行训练，最后得到某一个点的阈值为该点两个模型预测量的平均值。

5.二维码的编码

图 2 二维码生成图像

完成二维码的解码后，下一步需要检测该二维码是否有效，二维码的编码系统主要起到作用：

• 使具有显著特征的二维码数量最大；

• 尽可能多的检测出二维码的错误并修改；

• 减小错误野值二维码的数量；

• 减小二维码比特数。

通常以上的几项要求是互相矛盾的，当减小二维码比特数时，该二维码被识别的显著性就随之降低。本文直接使用了已经编码好的二维码，所以本方案主要使用该编码系统来过滤掉false postive，解码出错误的二维码将会直接导致估计的错误，该编码系统能够直接有效的提高位姿估计精度。二维码的编码是基于字典码 (lexicode)，字典码的由来受到字典中单词的启发：字典中单词按照字母的顺序从小到大排序，新的单词必须与上一次加入的单词之间的距离为d。字典码具有以下两个参数：编码的比特数n和两个字典码之间最小的海明距离 (Hamming distance)，字典码能够矫正 ⌊(d − 1)/2⌋ 并且检测d/2比特数。为了方便，将比特数为36最小海明距离为10的编码记为36h10。

对于二维码的编码，它必须对旋转鲁棒：二维码无论旋转 90o，180o 或者 270o都要保持与其他的二维码之间的最短距离为d。然而，经典的字典码不具备这样的特性，所以需要对经典的字典码加一条约束：当加入新的编码方式时，保证该编码在旋转四次时与其他的编码的距离至少为d。

存在一部分编码方式，即使能够满足字典码的距离约束，但是它也不能加入整个字库，例如全部为0的单词能够保持与其他单词的海明距离至少为10，但是它在图像上全部为黑色，在自然环境中存在很多相似的模式。为了剔除掉过于简单的几何模式，采用黑白相间的矩形排列模式。从理论上分析，高复杂度的二维码模式在自然界出现的频率更低。

总结起来，最终选取字典码来生成任意大小二维码的每一个bit，例如3×3，4×4 等，这样的方法不仅能够保证二维码对检测的旋转鲁棒性，还能够剔除低集合复杂度的编码方式。通常二维码的生成比较耗时，必须离线进行。对于5×5的二维码在几分钟内可以计算得到，但是利用CPU生成6×6二维码则需要花费数天的时间。

详见https://zhuanlan.zhihu.com/p/53367734