PyTorch基础知识 | 安装 | 张量 | 自动求导

---

PyTorch基础篇：

• PyTorch基础知识 | 安装 | 张量 | 自动求导
• PyTorch主要组成模块 | 数据读入 | 数据预处理 | 模型构建 | 模型初始化 | 损失函数 | 优化器 | 训练与评估
• PyTorch主要组成模块 | hook函数 | 正则化weight decay与Dropout | 标准化
• PyTorch模型定义 | 模型容器 | 模型块 | 修改模型 | 模型读取与保存
• PyTorch进阶技巧 | 自定义损失函数 | 动态调整学习率 | 模型微调 | 半精度训练 | 使用argparse进行调参
• PyTorch可视化 | 可视化网络结构 | 使用TensorBoard可视化训练过程

---

一、PyTorch安装

  这里介绍两种安装方式：

1.基于whl安装

  https://download.pytorch.org/whl/torch_stable.html下载对应cuda版本或cpu，对应pytorch版本，对应python版本、对应电脑系统的文件，选择两个文件torch与torchvision，然后在对应的虚拟环境下pip安装即可。

2.官网命令行安装

  https://pytorch.org/get-started/previous-versions/选择对应cuda版本或cpu，对应pytorch版本，对应python版本、对应电脑系统的命令。每个版本都有两种安装方式：conda和wheel。网速快的话，wheel方式更快一点。

二、张量

1.张量的简介

  张量的核心就是一个数据容器。

张量维度	代表含义
0维张量	代表的是标量（数字）
1维张量	代表的是向量
2维张量	代表的是矩阵
3维张量	时间序列数据 、股价、 文本数据、单张彩色图片(RGB)
4维张量	多张彩色图片(RGB)
5维张量	视频

  多数情况下，它只包含数字。在PyTorch中， 张量(torch.Tensor) 是存储和变换数据的主要工具。Tensor 提供GPU计算和自动求梯度等更多功能。
  Tensor有8个属性：

• data:被包装的Tensor
• dtype:张量的数据类型，如torch.FloatTensor, torch.cuda.FloatTensor(表示数据放到了GPU上)
• shape:张量的形状，如(64，3，224，224)
• device:张量所在设备，GPU/CPU，是加速的关键
• grad: data的梯度
• grad_fn:创建Tensor的Function，是自动求导的关键
• requires_grad:指示是否需要梯度
• is_leaf:指示是否是叶子结点（张量)

2.创建tensor

  常见的构造Tensor的方法如下：

函数	功能
Tensor(sizes)	基础构造函数
tensor(data)	data可以传入list, tuple,ndarray, scalar等，返回tensor
ones(sizes)	全1
zeros(sizes)	全0
eye(sizes)	对角为1，其余为0
arange(s,e,step)	从s到e，步长为step
linspace(s,e,steps)	从s到e，均匀分成step份
rand/randn(sizes)	rand是[0,1)均匀分布；randn是服从N(0，1)的正态分布
normal(mean,std)	正态分布(均值为mean，标准差是std)
randperm(m)	随机排列

2.1 直接创建

  torch.tensor()：直接传入数据list, tuple,ndarray, scalar等，构造一个张量。

torch.tensor(data, dtype=None, device=None, requires_grad=False,pin_memory=False)

功能：从data创建tensor

• data:数据，可以是list, tuple,ndarray, scalar
• dtype:数据类型，默认与data的一致
• device :所在设备，cuda/cpu
• requires_grad:是否需要梯度
• pin_memory:是否存于锁页内存（这与转换效率有关）

注意：torch.tensor创建得到的张量和原数据是不共享内存的，张量对应的变量是独立变量。

传入列表：

import torch
x = torch.tensor([5.5, 3]) 
print(x)

tensor([5.5000, 3.0000])

传入ndarry：

# tensor和numpy array之间的相互转换
import numpy as np

g = np.array([[1,2,3],[4,5,6]])
h = torch.tensor(g)
print(h)

tensor([[1, 2, 3],
        [4, 5, 6]], dtype=torch.int32)

  通过torch.from_numpy()创建张量

torch.from_numpy(ndarray)

注意事项：从torch.from_numpy创建的tensor与原ndarray共享内存，当修改其中一个的数据，另外一个也将会被改动。

import torch
import numpy as np
arr = np.ones((2, 2))
t1 = torch.from_numpy(arr)
print(arr)
print(t1)
t1 += 1
print(arr)
print(t1)

[[1. 1.]
 [1. 1.]]
tensor([[1., 1.],
        [1., 1.]], dtype=torch.float64)
[[2. 2.]
 [2. 2.]]
tensor([[2., 2.],
        [2., 2.]], dtype=torch.float64)

2.2 依据数值创建

  torch.zeros()：创建全0张量

torch.zeros(*size,
	out=None,dtype=None,
	layout=torch.strided,device=None,
	requires_grad=False)

功能:依size创建全0张量

• size:张量的形状，如(3，3)、(3，224,224)
• out:输出的张量
• layout :内存中布局形式，有strided,sparse_coo等
• device :所在设备，gpu/cpu
• requires_grad:是否需要梯度

  torch.zeros_like()

torch.zeros_like( input,
	dtype=None,layout=None,device=None,
	requires_grad=False)

功能:依input形状创建全0张量

• intput:创建与input同形状的全0张量
• dtype:数据类型
• layout :内存中布局形式

  torch.ones(),torch.ones_like()：创建全1张量

torch.ones( *size,
	out=None,dtype=None,
	layout=torch.strided,device=None,
	requires_grad=False)

功能:依size创建全1张量

torch.ones_like( input,
	dtype=None,layout=None,device=None,
	requires_grad=False)

功能:依input形状创建全1张量

• size:张量的形状，如(3，3)、(3，224,224)
• dtype:数据类型
• layout :内存中布局形式
• device :所在设备，gpu/cpu
• requires_grad:是否需要梯度

  torch.full(),torch.full_like()：创建指定数据的张量

torch.full(size,
	fill_value,out=None,dtype=None,
	layout=torch.strided,device=None,
	requires_grad=False)

功能:依input形状创建指定数据的张量

• size:张量的形状,如(3，3)
• fill_value:张量的值

t2 = torch.full((3, 3), fill_value=10)
print(t2)

#tensor([[10., 10., 10.],
#        [10., 10., 10.],
#        [10., 10., 10.]])

  torch.arange()：创建等差张量

torch.arange(start=0,
	end,step=1,
	out=None,dtype=None,
	layout=torch.strided ,device=None,
	requires_grad=False)

功能:创建等差的1维张量
注意事项:数值区间为[start, end),start:数列起始值,end:数列“结束值”,step:数列公差，默认为1

t3 = torch.arange(2, 10, 2)
print(t3)
# tensor([2, 4, 6, 8])

  torch.linspace()：创建均分的1维张量

torch.linspace(start,
	end,
	steps=100,out=None,dtype=None,
	layout=torch.strided,device=None,
	requires_grad=False)

功能:创建均分的1维张量
注意:数值区间为[start, end]，start:数列起始值，end :数列结束值，steps:数列长度
  torch.logspace()：创建对数均分的1维张量

torch. logspace(start,end,
	steps=100,base=10.0,out=None,dtype=None,
	layout=torch.strided,device=None,
	requires_grad=False)

功能:创建对数均分的1维张量
注意:长度为steps，底为base；start:数列起始值，end :数列结束值，steps:数列长度，base :对数函数的底，默认为10
  torch.eye()：创建单位对角矩阵

torch.eye(n,
	m=None,out=None,dtype=None,
	layout=torch.strided,device=None,
	requires_grad=False)

功能:创建单位对角矩阵（2维张量)
注意:默认为方阵；n:矩阵行数，m:矩阵列数

2.3 依概率分布创建

  torch.normal()：生成正态分布的张量。

torch.normal(mean,
	std,
	out=None)

功能:生成正态分布（高斯分布)；mean :均值，std :标准差
四种模式:

• mean为标量,std为标量
• mean为标量，std为张量
• mean为张量， std为标量
• mean为张量，std为张量

# mean：张量 std: 张量
mean = torch.arange(1, 5, dtype=torch.float)
std = torch.arange(1, 5, dtype=torch.float)
t_normal = torch.normal(mean, std)
print("mean:{}\nstd:{}".format(mean, std))
print(t_normal)

# mean：标量 std: 标量
t_normal = torch.normal(0., 1., size=(4,))
print(t_normal)

# mean：张量 std: 标量
mean = torch.arange(1, 5, dtype=torch.float)
std = 1
t_normal = torch.normal(mean, std)
print("mean:{}\nstd:{}".format(mean, std))
print(t_normal)

mean:tensor([1., 2., 3., 4.])
std:tensor([1., 2., 3., 4.])
tensor([0.3966, 1.5400, 0.7993, 9.4299])
tensor([-0.0378, -0.6219, -0.1607, -1.1813])
mean:tensor([1., 2., 3., 4.])
std:1
tensor([ 2.0800, -0.3626,  2.8807,  5.2153])

  torch.randn()，torch.randn_like()：生成标准正态分布的张量

torch.randn(*size,
	out=None,dtype=None,
	layout=torch.strided,device=None,
	requires_grad=False)

功能:生成标准正态分布；size :张量的形状
  torch.rand(),torch.rand_like()：生成区间[0，1)上均匀分布的张量。

torch.rand(*size,
	out=None,dtype=None,
	layout=torch. strided ,device=None,
	requires_grad=False)

功能:在区间[0，1)上,生成均匀分布
  torch.randint()，torch.randint_like()：生成区间[low,high)上整数均匀分布的张量。

torch.randint(low=0,
	high,size,
	out=None,dtype=None,
	layout=torch.strided,device=None,
	requires grad=False)

功能:区间[low,high)生成整数均匀分布； size :张量的形状
  torch.randperm()：生成从0到n-1的随机排列

torch.randperm(n,
	out=None,
	dtype=torch.int64,layout=torch.strided ,device=None,
	requires_grad=False)

功能:生成从0到n-1的随机排列；n:张量的长度

x = torch.randperm(5)
print(x)

tensor([0, 4, 3, 2, 1])

  torch.bernoulli()：以input为概率，生成伯努利分布的张量

torch.bernoulli(input,
*,
generator=None,
out=None)

功能:以input为概率，生成伯努利分布(0-1分布，两点分布)；input :概率值

3.张量的操作

  张量的操作这一部分包括张量的拼接、切分、索引、变换以及数学运算

3.1 张量的拼接

  张量的拼接有两个方法：torch.cat()与torch.stack()，cat方法不会拓展张量维度，而stack方法会拓展张量的维度。
  torch.cat()：将张量序列按维度dim进行拼接

torch.cat(tensors,
	dim=0,out=None)

• tensors:张量序列
• dim :要拼接的维度

  # torch.cat()
  t = torch.ones((2, 3))
  t_1 = torch.cat((t, t), dim=0)
  t_2 = torch.cat((t, t), dim=1)
  print("t_1:{},\nt_1.shape:{}\nt_2:{},\nt_2.shape:{}".format(t_1, t_1.shape, t_2, t_2.shape))
  

  t_1:tensor([[1., 1., 1.],
          [1., 1., 1.],
          [1., 1., 1.],
          [1., 1., 1.]]),
  t_1.shape:torch.Size([4, 3])
  t_2:tensor([[1., 1., 1., 1., 1., 1.],
          [1., 1., 1., 1., 1., 1.]]),
  t_2.shape:torch.Size([2, 6])
  

  torch.stack()：在新创建的维度dim上进行拼接

torch.stack (tensors,
	dim=0,out=None)

• tensors:张量序列

• dim :要拼接的维度

  t = torch.ones((2, 3))
  t_stack = torch.stack((t, t), dim=2)
  print('t_stack:{},\nt_stack.shape:{}'.format(t_stack, t_stack.shape))
  

  t_stack:tensor([[[1., 1.],
           [1., 1.],
           [1., 1.]],
  
          [[1., 1.],
           [1., 1.],
           [1., 1.]]]),
  t_stack.shape:torch.Size([2, 3, 2])
  

3.2 张量的切分

  张量的切分有两个方法：torch.chunk()与torch.split()
  torch.chunk()：将张量按维度dim进行平均切分

torch.chunk (input,
	chunks,dim=0)

返回值:张量列表
注意:若不能整除,最后一份张量小于其他张量

• input:要切分的张量

• chunks :要切分的份数

• dim:要切分的维度

  t = torch.ones((2, 5))
  list_of_tensor = torch.chunk(t, dim=1, chunks=2)
  for idx, tensor in enumerate(list_of_tensor):
      print('第{}个张量:{},shape:{}'.format(idx, tensor, tensor.shape))
  

  第0个张量:tensor([[1., 1., 1.],
          [1., 1., 1.]]),shape:torch.Size([2, 3])
  第1个张量:tensor([[1., 1.],
          [1., 1.]]),shape:torch.Size([2, 2])
  

  torch.split()：将张量按维度dim进行切分

torch.split(tensor,
	split_size_or_sections,dim=0)

返回值:张量列表

• tensor:要切分的张量

• split_size_or_sections : 为int时,表示每一份的长度;为list时,按list元素切分

• dim:要切分的维度

  t = torch.ones((2, 5))
  list_of_tensor = torch.split(t, [2, 1, 2], dim=1)
  for idx, tensor in enumerate(list_of_tensor):
      print('第{}个张量:{},shape:{}'.format(idx, tensor, tensor.shape))
  

  第0个张量:tensor([[1., 1.],
          [1., 1.]]),shape:torch.Size([2, 2])
  第1个张量:tensor([[1.],
          [1.]]),shape:torch.Size([2, 1])
  第2个张量:tensor([[1., 1.],
          [1., 1.]]),shape:torch.Size([2, 2])
  

3.3 张量的索引

  张量的索引有如下方法：torch.index_select() 与torch.masked_select()
  torch.index_select()：在维度dim上，按index索引数据

torch.index_select(input,
	dim,index,out=None)

返回值:依index索引数据拼接的张量

• input:要索引的张量

• dim:要索引的维度

• index:要索引数据的序号

  # 3*3的均匀分布
  t = torch.randint(0, 9, size=(3, 3))
  # 生成索引序号-torch.long64位的整型
  idx = torch.tensor([0, 2], dtype=torch.long)
  # 依据索引选择数据
  t_select = torch.index_select(t, dim=1, index=idx)
  print('t:\n{}\nt_select:\n{}'.format(t, t_select))
  

  t:
  tensor([[8, 1, 2],
          [4, 2, 5],
          [3, 4, 7]])
  t_select:
  tensor([[8, 2],
          [4, 5],
          [3, 7]])
  

  torch.masked_select()：按mask中的True进行索引

torch.masked_select(input,
	mask,
	out=None)

返回值:一维张量

• input:要索引的张量

• mask: 与input同形状的布尔类型张量

  # 3*3的均匀分布
  t = torch.randint(0, 9, size=(3, 3))
  # ge:大于等于；gt:大于
  mask = t.ge(5)
  t_select = torch.masked_select(t, mask)
  print('t:\n{}\nmask:\n{}\nt_select:\n{}'.format(t, mask, t_select))
  

  t:
  tensor([[0, 7, 7],
          [5, 6, 5],
          [6, 7, 1]])
  mask:
  tensor([[False,  True,  True],
          [ True,  True,  True],
          [ True,  True, False]])
  t_select:
  tensor([7, 7, 5, 6, 5, 6, 7])
  

3.4 张量的变换

  张量的变换包括：torch.view()与torch.reshape() 与torch.transpose()与torch.t()与torch.squeeze()与torch.unsqueeze()
  torch.view()：变换张量形状
注意：torch.view() 返回的新tensor与源tensor共享内存(其实是同一个tensor)，更改其中的一个，另外一个也会跟着改变。(顾名思义，view()仅仅是改变了对这个张量的观察角度)

x = torch.randn(4, 4)
y = x.view(16)
z = x.view(-1, 8) # -1是指这一维的维数由其他维度决定
print(x.size(), y.size(), z.size())

torch.Size([4, 4]) torch.Size([16]) torch.Size([2, 8])

x += 1
print(x)
print(y) # 也加了了1

tensor([[ 1.1434,  0.2632,  1.8236,  0.3194],
        [ 1.3223,  1.3341,  1.9673,  1.2045],
        [ 0.7703,  1.5630,  1.2670,  2.3715],
        [ 1.2348,  1.5063, -0.0090,  0.0617]])
tensor([ 1.1434,  0.2632,  1.8236,  0.3194,  1.3223,  1.3341,  1.9673,  1.2045,
         0.7703,  1.5630,  1.2670,  2.3715,  1.2348,  1.5063, -0.0090,  0.0617])

上面我们说过torch.view()会改变原始张量，但是很多情况下，我们希望原始张量和变换后的张量互相不影响。为了使创建的张量和原始张量不共享内存，官方推荐的方法是我们先用 clone() 创造一个张量副本然后再使用 torch.view()进行函数维度变换 。
注意：使用 clone() 还有一个好处是会被记录在计算图中，即梯度回传到副本时也会传到源 Tensor。

x = torch.randn(4, 4)
x_ = x.clone()
y = x_.view(2,8)
x += 1
print(x)
print(y)

tensor([[ 0.8350,  0.6267,  1.5454,  1.6257],
        [ 1.6424, -0.9586,  2.2201,  2.6465],
        [-0.2895,  0.7816,  0.8534,  1.8767],
        [-0.9261,  1.7207,  0.6599, -0.2106]])
tensor([[-0.1650, -0.3733,  0.5454,  0.6257,  0.6424, -1.9586,  1.2201,  1.6465],
        [-1.2895, -0.2184, -0.1466,  0.8767, -1.9261,  0.7207, -0.3401, -1.2106]])

  torch.reshape() :变换张量形状

torch.reshape(input,
	shape)

注意:当张量在内存中是连续时,新张量与input共享数据内存

如果两个变量之间共享内存，那么改变其中一个变量的同时，另一个变量也会改变

• input:要变换的张量

• shape:新张量的形状

  # 生成随机排列
  t = torch.randperm(8)
  t_reshape = torch.reshape(t, (2, 4))
  print('t:\n{}\nt_reshape:\n{}'.format(t, t_reshape))
  

  t:
  tensor([1, 3, 5, 2, 7, 4, 0, 6])
  t_reshape:
  tensor([[1, 3, 5, 2],
          [7, 4, 0, 6]])
  

  torch.transpose()：交换张量的两个维度

torch.transpose(input,
	dim0,dim1)

• input:要变换的张量

• dim0:要交换的维度

• dim1:要交换的维度

  t = torch.rand((2, 3, 4))
  t_transpose = torch.transpose(t, dim0=1, dim1=2)    # c*h*w  =>  c*w*h
  print("t shape:{}\nt_transpose shape: {}".format(t.shape, t_transpose.shape))
  

  t shape:torch.Size([2, 3, 4])
  t_transpose shape: torch.Size([2, 4, 3])
  

  torch.t()：2维张量转置,对矩阵而言,等价于torch.transpose(input,0，1)

torch.t(input)

  torch.squeeze()：压缩长度为1的维度(轴)

torch.squeeze(input,
	dim=None,out=None)

• dim:若为None，移除所有长度为1的轴;若指定维度，当且仅当该轴长度为1时,可以被移除

  t = torch.rand((1, 2, 3, 1))
  # dim为None
  t_sq = torch.squeeze(t)
  # dim=0时长度为1
  t_0 = torch.squeeze(t, dim=0)
  # dim=1时长度不为1
  t_1 = torch.squeeze(t, dim=1)
  print(t.shape)
  print(t_sq.shape)
  print(t_0.shape)
  print(t_1.shape)
  

  torch.Size([1, 2, 3, 1])
  torch.Size([2, 3])
  torch.Size([2, 3, 1])
  torch.Size([1, 2, 3, 1])
  

  torch.unsqueeze()：依据dim扩展维度

torch.usqueeze( input,
	dim,
	out=None)

• dim:扩展的维度

  t_unsq = torch.unsqueeze(t_sq, dim=0)
  print(t_sq.shape)
  print(t_unsq.shape)
  

  torch.Size([2, 3])
  torch.Size([1, 2, 3])
  

3.5 张量的数学运算

  PyTorch中提供大量的数学运算，大致可以分为三类：

• 加减乘除

  torch.add()
  torch.addcdiv()
  torch.addcmul()
  torch.sub()
  torch.div()
  torch.mu()
  

  torch.add()：逐元素计算input + alpha × other

  torch.add(input,
  	alpha=1,other,out=None)
  

  • input:第一个张量
  • alpha:乘项因子
  • other:第二个张量

  torch.addcmul()：

  torch.addcmul(input,
  		value=1,tensor1,tensor2,out=None)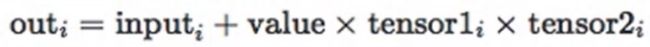
  

  
  torch.addcdiv()：
  

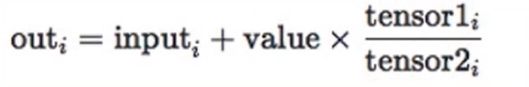
• 对数指数幂函数

  torch.log(input,out=None)
  torch.log10(input, out=None)
  torch.log2(input, out=None)
  torch.exp(input,out=None)
  torch.pow()
  

• 三角函数

  torch.abs(input, out=None)
  torch.acos(input, out=None)
  torch.cosh(input, out=None)
  torch.cos(input, out=None)
  torch.asin(input, out=None)
  torch.atan(input, out=None)
  torch.atan2(input, other, out=None)
  

PyTorch中的 Tensor 支持超过一百种操作，包括转置、索引、切片、数学运算、线性代数、随机数等等，具体使用方法可参考TORCH.TENSOR。

4.广播机制

  当对两个形状不同的 Tensor 按元素运算时，可能会触发广播(broadcasting)机制：先适当复制元素使这两个 Tensor 形状相同后再按元素运算。

import torch
x = torch.arange(1, 3).view(1, 2)
print(x)
y = torch.arange(1, 4).view(3, 1)
print(y)
print(x + y)

tensor([[1, 2]])
tensor([[1],
        [2],
        [3]])
tensor([[2, 3],
        [3, 4],
        [4, 5]])

由于x和y分别是1行2列和3行1列的矩阵，如果要计算x+y，那么x中第一行的2个元素被广播 (复制)到了第二行和第三行，⽽y中第⼀列的3个元素被广播(复制)到了第二列。如此，就可以对2个3行2列的矩阵按元素相加。

5.is_leaf与grad_fn概念

  我们可以知道Tensor中有叶子节点is_leaf与grad_fn的概念。

叶子结点︰用户创建的结点称为叶子结点，如$x与w$
is_leaf:指示张量是否为叶子结点

  为什么要设置叶子节点这一概念？主要是为了节省内存，在梯度反向传播之后，非叶子节点的梯度是会被释放掉的。以$y=(x+w)\ast (w+1)$为例，

import torch

# 需要计算梯度-requires_grad=True
w = torch.tensor([1.], requires_grad=True)
x = torch.tensor([2.], requires_grad=True)

# 前向传播
a = torch.add(w, x)     # retain_grad()
b = torch.add(w, 1)
y = torch.mul(a, b)

# 反向传播-自动求导
y.backward()
print(w.grad)

# 查看叶子结点
print("is_leaf:\n", w.is_leaf, x.is_leaf, a.is_leaf, b.is_leaf, y.is_leaf)

# 查看梯度
print("gradient:\n", w.grad, x.grad, a.grad, b.grad, y.grad)

is_leaf:
 True True False False False
gradient:
 tensor([5.]) tensor([2.]) None None None

  如果我们想要保存非叶子节点的梯度，那么应该怎么做呢？使用.retain_grad()

import torch

# 需要计算梯度-requires_grad=True
w = torch.tensor([1.], requires_grad=True)
x = torch.tensor([2.], requires_grad=True)

# 前向传播
a = torch.add(w, x)     
# 保存非叶子节点a的梯度
a.retain_grad()
b = torch.add(w, 1)
y = torch.mul(a, b)

# 反向传播-自动求导
y.backward()
print(w.grad)

# 查看叶子结点
print("is_leaf:\n", w.is_leaf, x.is_leaf, a.is_leaf, b.is_leaf, y.is_leaf)

# 查看梯度
print("gradient:\n", w.grad, x.grad, a.grad, b.grad, y.grad)

tensor([5.])
is_leaf:
 True True False False False
gradient:
 tensor([5.]) tensor([2.]) tensor([2.]) None None

  grad_fn:记录创建该张量时所用的方法(函数)，是自动求导的关键。

import torch

# 需要计算梯度-requires_grad=True
w = torch.tensor([1.], requires_grad=True)
x = torch.tensor([2.], requires_grad=True)

# 前向传播
a = torch.add(w, x)
# 保存非叶子节点a的梯度
a.retain_grad()
b = torch.add(w, 1)
y = torch.mul(a, b)

# 反向传播-自动求导
y.backward()
print(w.grad)

# 查看创建张良所使用的函数
print("grad_fn:\n", w.grad_fn, x.grad_fn, a.grad_fn, b.grad_fn, y.grad_fn)

tensor([5.])
grad_fn:
 None None <AddBackward0 object at 0x0000021BCD8FB710> <AddBackward0 object at 0x0000021BCD900128> <MulBackward0 object at 0x0000021BCD9000F0>

三、自动求导

  PyTorch 中，所有神经网络的核心是 autograd 包。autograd包为张量上的所有操作提供了自动求导机制。它是一个在运行时定义 ( define-by-run ）的框架，这意味着反向传播是根据代码如何运行来决定的，并且每次迭代可以是不同的。

1.Autograd简介

  torch.Tensor 是这个包的核心类。如果设置它的属性 .requires_grad 为 True，那么它将会追踪对于该张量的所有操作。当完成计算后可以通过调用 .backward()，来自动计算所有的梯度。这个张量的所有梯度将会自动累加到.grad属性。
注意：在 y.backward() 时，如果 y 是标量，则不需要为 backward() 传入任何参数；否则，需要传入一个与 y 同形的Tensor。
  要阻止一个张量被跟踪历史，可以调用.detach()方法将其与计算历史分离，并阻止它未来的计算记录被跟踪。为了防止跟踪历史记录(和使用内存），可以将代码块包装在 with torch.no_grad(): 中。在评估模型时特别有用，因为模型可能具有 requires_grad = True 的可训练的参数，但是我们不需要在此过程中对他们进行梯度计算。
  还有一个类对于autograd的实现非常重要：Function。Tensor 和 Function 互相连接生成了一个无环图 (acyclic graph)，它编码了完整的计算历史。每个张量都有一个.grad_fn属性，该属性引用了创建 Tensor 自身的Function(除非这个张量是用户手动创建的，即这个张量的grad_fn是 None )。下面给出的例子中，张量由用户手动创建，因此grad_fn返回结果是None。

import torch
x = torch.randn(3,3,requires_grad=True)
print(x.grad_fn)

None

  如果需要计算导数，可以在 Tensor 上调用 .backward()。如果 Tensor 是一个标量(即它包含一个元素的数据），则不需要为 backward() 指定任何参数，但是如果它有更多的元素，则需要指定一个gradient参数，该参数是形状匹配的张量。
  创建一个张量并设置requires_grad=True用来追踪其计算历史。

import torch
x = torch.ones(2, 2, requires_grad=True)
print(x)

tensor([[1., 1.],
        [1., 1.]], requires_grad=True)

对这个张量做一次运算。

y = x**2
print(y)
print(y.grad_fn)

tensor([[1., 1.],
        [1., 1.]], grad_fn=<PowBackward0>)
<PowBackward0 object at 0x00000204E1360588>

y是计算的结果，所以它有grad_fn属性。对 y 进行更多操作

z = y * y * 3
out = z.mean()

print(z, out)

tensor([[3., 3.],
        [3., 3.]], grad_fn=<MulBackward0>) tensor(3., grad_fn=<MeanBackward0>)

  .requires_grad_(...) 原地改变了现有张量的requires_grad标志。如果没有指定的话，默认输入的这个标志是 False。

import torch
a = torch.randn(2, 2) # 缺失情况下默认 requires_grad = False
a = ((a * 3) / (a - 1))
print(a.requires_grad)
a.requires_grad_(True)
print(a.requires_grad)
b = (a * a).sum()
print(b.grad_fn)

False
True
<SumBackward0 object at 0x00000204FCF0CC88>

2.torch.autograd—自动求导系统

注意：grad在反向传播过程中是累加的(accumulated)，这意味着每一次运行反向传播，梯度都会累加之前的梯度，所以一般在反向传播之前需把梯度清零。
  深度学习模型的训练就是不断更新权值。权值的更新需要求解梯度。PyTorch提供自动求导系统解决这一问题。自动求导系统autograd只需要搭建前向传播的计算图，然后通过torch.autograd就可以得到每个张量的梯度。下面我们讲解torch.autograd中的方法。
  torch.autograd.backward()：自动求取梯度。

torch.autograd.backward(tensors,
	grad_tensors=None,
	retain_graph=None,create_graph=False)

• tensors:用于求导的张量,如loss

• retain_graph :保存计算图（如果想多次使用计算图）

• create_graph :创建导数计算图,用于高阶求导

• grad_tensors:多梯度权重（用于多个梯度权重的设置）

  w = torch.tensor([1.], requires_grad=True)
  x = torch.tensor([2.], requires_grad=True)
  
  a = torch.add(w, x)     # retain_grad()
  b = torch.add(w, 1)
  
  y0 = torch.mul(a, b)    # y0 = (x+w) * (w+1)
  y1 = torch.add(a, b)    # y1 = (x+w) + (w+1)    dy1/dw = 2
  
  loss = torch.cat([y0, y1], dim=0)       # [y0, y1]
  grad_tensors = torch.tensor([1., 2.])
  
  loss.backward(gradient=grad_tensors)    # gradient 传入 torch.autograd.backward()中的grad_tensors
  
  print(w.grad)
  

  tensor([9.])	
  

  torch.autograd.grad()：求取梯度。

torch.autograd.grad(outputs,
	inputs,grad_outputs=None,
	retain_graph=None,create_graph=False)

• outputs: 用于求导的张量，如 loss

• inputs :需要梯度的张量

• create_graph :创建导数计算图,用于高阶求导

• retain_graph :保存计算图

• grad_outputs:多梯度权重

  x = torch.tensor([3.], requires_grad=True)
  y = torch.pow(x, 2)     # y = x**2
  
  grad_1 = torch.autograd.grad(y, x, create_graph=True)   # grad_1 = dy/dx = 2x = 2 * 3 = 6
  print(grad_1)
  
  grad_2 = torch.autograd.grad(grad_1[0], x)              # grad_2 = d(dy/dx)/dx = d(2x)/dx = 2
  print(grad_2)
  

  (tensor([6.], grad_fn=<MulBackward0>),)
  (tensor([2.]),)
  

torch.autograd()中需要注意如下几点：

1. 梯度不自动清零,需要手动清零

   w = torch.tensor([1.], requires_grad=True)
   x = torch.tensor([2.], requires_grad=True)
   
   for i in range(4):
       a = torch.add(w, x)
       b = torch.add(w, 1)
       y = torch.mul(a, b)
   
       y.backward()
       print(w.grad)
       # 梯度清零
       # w.grad.zero_()
   

   	tensor([5.])
   	tensor([10.])
   	tensor([15.])
   	tensor([20.])
   

   w = torch.tensor([1.], requires_grad=True)
   x = torch.tensor([2.], requires_grad=True)
   
   for i in range(4):
       a = torch.add(w, x)
       b = torch.add(w, 1)
       y = torch.mul(a, b)
   
       y.backward()
       print(w.grad)
       # 梯度清零
       w.grad.zero_()
   

   tensor([5.])
   tensor([5.])
   tensor([5.])
   tensor([5.])
   

2. 依赖于叶子节点的节点，requires_grad默认为True

   w = torch.tensor([1.], requires_grad=True)
   x = torch.tensor([2.], requires_grad=True)
   
   a = torch.add(w, x)
   b = torch.add(w, 1)
   y = torch.mul(a, b)
   
   print(a.requires_grad, b.requires_grad, y.requires_grad)
   

   True True True
   

3. 叶子节点不可执行in-place（原地操作）

四、并行计算简介

  在利用PyTorch做深度学习的过程中，可能会遇到数据量较大无法在单块GPU上完成，或者需要提升计算速度的场景，这时就需要用到并行计算。

1.为什么要做并行计算?

  深度学习的发展离不开算力的发展，GPU的出现让我们的模型可以训练的更快，更好。所以，如何充分利用GPU的性能来提高我们模型学习的效果就需要用到PyTorch的并行计算。PyTorch可以在编写完模型之后，让多个GPU来参与训练，减少训练时间。

2.为什么需要CUDA?

  CUDA是我们使用GPU的提供商——NVIDIA提供的GPU并行计算框架。对于GPU本身的编程，使用的是CUDA语言来实现的。但是，在我们使用PyTorch编写深度学习代码时，使用的CUDA又是另一个意思。在PyTorch使用 CUDA表示要开始要求我们的模型或者数据开始使用GPU了。
  在编写程序中，当我们使用了 .cuda() 时，其功能是让我们的模型或者数据从CPU迁移到GPU(0)当中，通过GPU开始计算。
注意：

1. 我们使用GPU时使用的是.cuda()而不是使用.gpu()。这是因为当前GPU的编程接口采用CUDA，但是市面上的GPU并不是都支持CUDA，只有部分NVIDIA的GPU才支持，AMD的GPU编程接口采用的是OpenCL，在现阶段PyTorch并不支持。

2. 数据在GPU和CPU之间进行传递时会比较耗时，我们应当尽量避免数据的切换。

3. GPU运算很快，但是在使用简单的操作时，我们应该尽量使用CPU去完成。

4. 当我们的服务器上有多个GPU，我们应该指明我们使用的GPU是哪一块，如果我们不设置的话，tensor.cuda()方法会默认将tensor保存到第一块GPU上，等价于tensor.cuda(0)，这将会导致爆出out of memory的错误。我们可以通过以下两种方式继续设置。

   #设置在文件最开始部分
   import os
   os.environ["CUDA_VISIBLE_DEVICE"] = "2" # 设置默认的显卡
   

    CUDA_VISBLE_DEVICE=0,1 python train.py # 使用0，1两块GPU
   

3.常见的并行的方法

1. 网络结构分布到不同的设备中(Network partitioning)
   在刚开始做模型并行的时候，这个方案使用的比较多。其中主要的思路是，将一个模型的各个部分拆分，然后将不同的部分放入到GPU来做不同任务的计算。其架构如下：
   
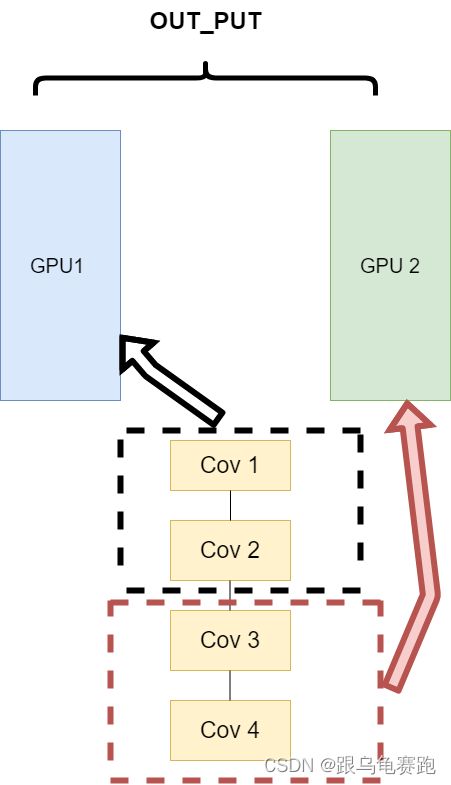
   这里遇到的问题就是，不同模型组件在不同的GPU上时，GPU之间的传输就很重要，对于GPU之间的通信是一个考验。但是GPU的通信在这种密集任务中很难办到，所以这个方式慢慢淡出了视野。
2. 同一层的任务分布到不同数据中(Layer-wise partitioning)
   第二种方式就是，同一层的模型做一个拆分，让不同的GPU去训练同一层模型的部分任务。其架构如下:
   
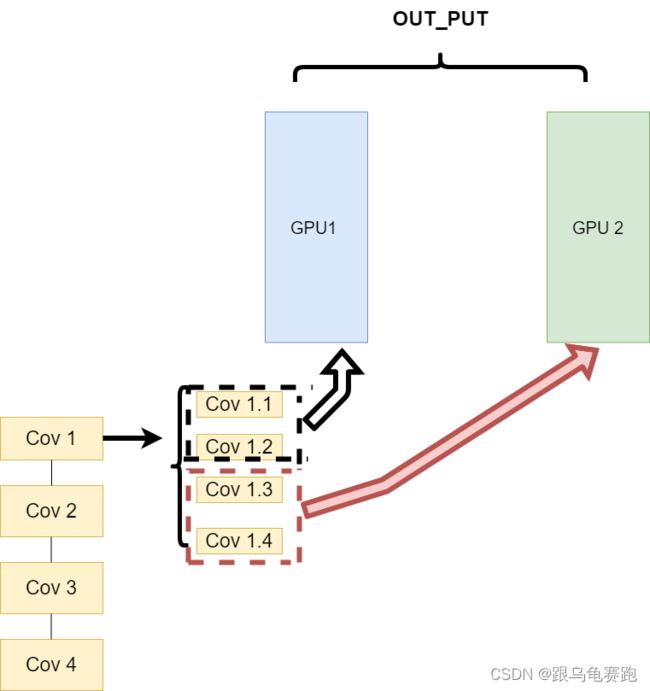
   这样可以保证在不同组件之间传输的问题，但是在我们需要大量的训练，同步任务加重的情况下，会出现和第一种方式一样的问题。
3. 不同的数据分布到不同的设备中，执行相同的任务(Data parallelism)
   第三种方式有点不一样，它的逻辑是，我不再拆分模型，我训练的时候模型都是一整个模型。但是我将输入的数据拆分。所谓的拆分数据就是，同一个模型在不同GPU中训练一部分数据，然后再分别计算一部分数据之后，只需要将输出的数据做一个汇总，然后再反传。其架构如下：
   
   这种方式可以解决之前模式遇到的通讯问题。现在的主流方式是数据并行的方式(Data parallelism)。

---

参考文献：

• https://github.com/datawhalechina/thorough-pytorch