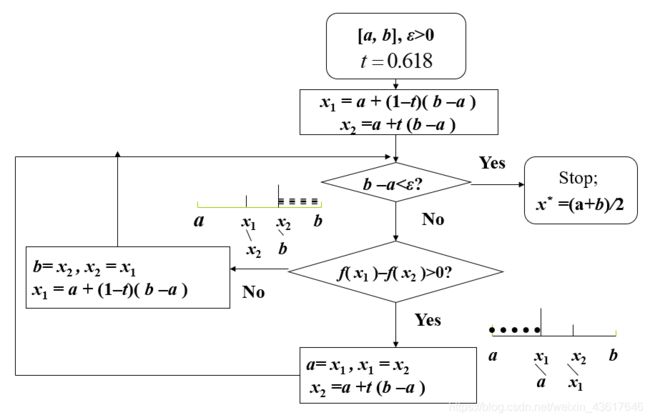
0.618（黄金分割法）求解极值点开源代码

0.618方法求解一元多次单峰函数极小点Python代码

1. 0.618方法寻找极值点流程框图
   
2. -直接上代码（python）

##定义待运算的目标函数，给他整成一元四次的类型，参数可自己通过键盘键入

##定义目标函数
def face(x):              
    return a1*x**4+b1*x**3+c1*x**2+d1*x+e1

##定义每一次迭代返回的结果
def Iteration(count,x1,x2,f1,f2,a,b,len):
    print("第",count, "次迭代")
    print("x1:{:.3f}     x2:{:.3f}     f1:{:.4f}      f2:{:.4f}      [a,b]:[{:.4f},{:.4f}]      |b-a|:{:.4f}".format(x1,x2,f1,f2,a,b,abs(b-a)))
    return count

##0.618法的核心，以0.618比例不断压缩区间，直到逼近精度为止
def HJFG(a,b,acu):  ##a,b为区间左右值，acu为收敛精度
    lamb=0.618  
    count=0    ##迭代次数
    x1=a+(1-lamb)*(b-a)   ##x1,x2 为区间内点，分别是区间的0.382和0.618分断点
    x2=a+lamb*(b-a)
    f1=face(x1)
    f2=face(x2)
    while (abs(b-a)>=acu) :
        count+=1
        if f1<=f2:  ##更新搜索区间
                b=x2
                len=b-a
                Iteration(count,x1,x2,f1,f2,a,b,len)
                if abs(b-a)<=acu:
                        print("函数极小点近似最优点为：",(b+a)/2)
                        Jmin=face((b+a)/2)
                        print("函数极小值为：",Jmin)
                        break 
                else:   
                        x2=x1      
                        x1=a+(1-lamb)*(b-a)   ##替换空间
        elif f1>f2:
                a=x1
                len=b-a
                Iteration(count,x1,x2,f1,f2,a,b,len)
                if abs(b-a)<acu:
                            print("函数极小点近似最优点为：",(b+a)/2)
                            Jmin=face((b+a)/2)
                            print("函数极小值为：",Jmin)
                            break
                else:       
                            x1=x2
                            x2=a+lamb*(b-a)
        f1=face(x1)
        f2=face(x2)
        
        
a1,b1,c1,d1,e1=map(float,input("请依次输入函数各参数").split(' '))
acu=float(input("输入收敛精度："))
print("目标函数为f(x)={}*x^4+{}*x^3+{}*x^2+{}*x+{}".format(a1,b1,c1,d1,e1))
a,b=map(float,input("输入区间长度[a,b]=：").split(' '))   
HJFG(a,b,acu)

3.演示结果

该图片中，给出了一个演示函数，实现了求解。其具体步骤：运行代码，键入参数，按下回车，得到输出结果。