辐射神经场算法——Wild-NeRF / Mipi-NeRF / BARF / NSVF / Semantic-NeRF / DSNeRF
辐射神经场算法——NeRF++ / Wild-NeRF / Mipi-NeRF / BARF / NSVF / Semantic-NeRF
- 辐射神经场算法——NeRF++ / Wild-NeRF / Mip-NeRF / BARF /NSVF / Semantic-NeRF / DSNeRF
-
- 1. NeRF++
- 2. Wild-NeRF
- 3. Mip-NeRF
- 4. BARF
- 5. NSVF
- 6. Semantic-NeRF
辐射神经场算法——NeRF++ / Wild-NeRF / Mip-NeRF / BARF /NSVF / Semantic-NeRF / DSNeRF
原始的NeRF虽然效果很惊艳,但是其一个场景少则一两天的训练速度,以及对于输入图像质量和位姿的要求却不尽人意,因此,在NeRF提出来很短的时间内就衍生出了各种基于NeRF优化的方法,本文主要是对这些方法进行一个简单总结,但是建议先了解原始NeRF的算法原理再来阅读本博客,对于原始NeRF算法的介绍可以参考博客辐射神经场算法——NeRF算法详解
1. NeRF++
NeRF++原论文名为《NeRF++: Analyzing and Improving Nerual Radiance Fileds》,该论文主要包括两部分:一部分是分析了原始NeRF具备的Shape-Radiance Ambiguity问题,另一部分是提出了一个解决室外360度开放场景的渲染方案。
首先针对Shape-Radiance Ambiguity问题,作者做了如下一个实验:

作者先使用一个球形的模型去训练NeRF中的 σ \sigma σ,然后再使用上左中的GT training view去训练NeRF中的 c \bold{c} c,在相同视角下进行预测时发现即使在错误的 σ \sigma σ分布下仍然能输出较好的图像质量,但是一旦更换视角(GT test view)就会输出如上左图的结果。造成该现象的原因正是View-Dependent的网络设计。但是如果我们一旦修改网络设计,将采样点的位置 x x x和方向 d \bold{d} d都从网络的第一层输入的话,网络整体效果就会下降,如下图所示:

文章的第二部分介绍的室外360度开放场景的一种解决方案,在原始NeRF中,对于Front-View的开放场景,使用的一种名为NDT坐标系的方式(可以简单理解为逆深度),但是对于360度的开放场景NDT坐标系是搞不定的,因此作者提出了将360度开放场景的渲染分为两部分通过两个NeRF进行渲染,如下所示:
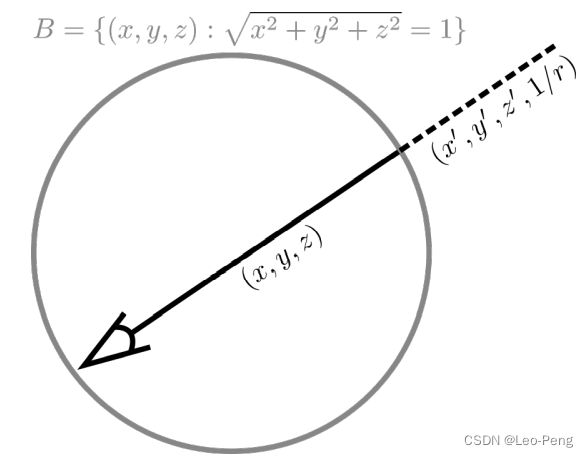
规定一个球体 B = { ( x , y , z ) : x 2 + y 2 + z 2 = 1 } B=\left\{(x, y, z): \sqrt{x^{2}+y^{2}+z^{2}}=1\right\} B={(x,y,z):x2+y2+z2=1}:
球体内保持欧拉坐标系 ( x , y , z ) (x, y, z) (x,y,z),使用原始的NeRF用于渲染前景部分;
球体外通过一个四维向量 ( x ′ , y ′ , z ′ , 1 / r ) \left(x^{\prime}, y^{\prime}, z^{\prime}, 1 / r\right) (x′,y′,z′,1/r)表示,用于渲染背景部分,其中 x ′ 2 + y ′ 2 + z ′ 2 = 1 x^{\prime 2}+y^{\prime 2}+z^{\prime 2}=1 x′2+y′2+z′2=1用于表示方向, 0 < 1 / r < 1 0<1 / r<1 0<1/r<1用于表示距离,并且 x ′ , y ′ , z ′ ∈ [ − 1 , 1 ] , 1 / r ∈ [ 0 , 1 ] x^{\prime}, y^{\prime}, z^{\prime} \in[-1,1], 1 / r \in[0,1] x′,y′,z′∈[−1,1],1/r∈[0,1],用于进行背景渲染的NeRF输入为 ( x ′ , y ′ , z ′ , 1 / r ) \left(x^{\prime}, y^{\prime}, z^{\prime}, 1 / r\right) (x′,y′,z′,1/r),输出则是 σ out , c out \sigma_{\text {out }}, \mathbf{c}_{\text {out }} σout ,cout .
那么接下来的问题就是当我们给定一个像素的射线 r = o + t d \mathbf{r}=\mathbf{o}+t \mathbf{d} r=o+td,当采样点位于球体外时如何求得四维向量 ( x ′ , y ′ , z ′ , 1 / r ) \left(x^{\prime}, y^{\prime}, z^{\prime}, 1 / r\right) (x′,y′,z′,1/r)呢?如下图所示:

我们给定不同采样点 p \mathbf{p} p得到不同的半径 r r r,那么如果获得 x ′ , y ′ , z ′ x^{\prime}, y^{\prime}, z^{\prime} x′,y′,z′呢?上图中点 a = o + t a d \mathbf{a}=\mathbf{o}+t_{a} \mathbf{d} a=o+tad,我们令 ∣ o + t a d ∣ = 1 \left|\mathbf{o}+t_{a} \mathbf{d}\right|=1 ∣o+tad∣=1就可以求得点 a \mathbf{a} a的坐标,同理点 b = o + t b d \mathbf{b}=\mathbf{o}+t_{b} \mathbf{d} b=o+tbd可以通过 d T ( o + t b d ) = 0 \mathbf{d}^{T}\left(\mathbf{o}+t_{b} \mathbf{d}\right)=0 dT(o+tbd)=0求得,那么我们根据 ω = arcsin ∣ b ∣ − arcsin ( ∣ b ∣ ⋅ 1 r ) \omega=\arcsin |\mathbf{b}|-\arcsin \left(|\mathbf{b}| \cdot \frac{1}{r}\right) ω=arcsin∣b∣−arcsin(∣b∣⋅r1)即可以对点 a \mathbf{a} a方向进行渲染既可以得到点 p \mathbf{p} p的方向 x ′ , y ′ , z ′ x^{\prime}, y^{\prime}, z^{\prime} x′,y′,z′,其实就是一个很简单的几何求解。解决了这个问题后就可以给出最后NeRF++的计算公式:
C ( r ) = ∫ t = 0 t ′ σ ( o + t d ) ⋅ c ( o + t d , d ) ⋅ e − ∫ s = 0 t σ ( o + s d ) d s d t ⏟ (i) + e − ∫ s = 0 t ′ σ ( o + s d ) d s ⏟ (ii) ⋅ ∫ t = t ′ ∞ σ ( o + t d ) ⋅ c ( o + t d , d ) ⋅ e − ∫ s = t ′ t σ ( o + s d ) d s d t ⏟ (iii) . \begin{aligned} \mathbf{C}(\mathbf{r})=& \underbrace{\int_{t=0}^{t^{\prime}} \sigma(\mathbf{o}+t \mathbf{d}) \cdot \mathbf{c}(\mathbf{o}+t \mathbf{d}, \mathbf{d}) \cdot e^{-\int_{s=0}^{t} \sigma(\mathbf{o}+s \mathbf{d}) d s} d t}_{\text {(i) }} \\ &+\underbrace{e^{-\int_{s=0}^{t^{\prime}} \sigma(\mathbf{o}+s \mathbf{d}) d s}}_{\text {(ii) }} \cdot \underbrace{\int_{t=t^{\prime}}^{\infty} \sigma(\mathbf{o}+t \mathbf{d}) \cdot \mathbf{c}(\mathbf{o}+t \mathbf{d}, \mathbf{d}) \cdot e^{-\int_{s=t^{\prime}}^{t} \sigma(\mathbf{o}+s \mathbf{d}) d s} d t}_{\text {(iii) }} . \end{aligned} C(r)=(i) ∫t=0t′σ(o+td)⋅c(o+td,d)⋅e−∫s=0tσ(o+sd)dsdt+(ii) e−∫s=0t′σ(o+sd)ds⋅(iii) ∫t=t′∞σ(o+td)⋅c(o+td,d)⋅e−∫s=t′tσ(o+sd)dsdt.从公式可以看出,背景和前景会分别渲染,然后背景会作为一个固定值加入到前景中,如下图所示:

2. Wild-NeRF
Wild-NeRF提出于2021年CVPR,原论文名称为《NeRF in the Wild: Neural Radiance Fields for Unconstrained Photo Collections》,Wild指的是室外场景,该论文主要解决的是原始NeRF在室外场景应用遇到的两个问题
- Variable Illumination:这个指的是,原始NeRF算法对于输入图片要求是光照条件具备一致性,而在室外的数据集上这一点是很难保证的,为此作者在原始MLP网络的基础上增加了Latent Appearance Modeling部分;
- Transition Occluders:这个指的是,在室外场景中拍摄经常会遇到动态物体这遮挡,在原始NeRF则是假设所有物体都是静止的,为此作者在原来MLP输出Intensity和Color的基础上增加了和动态物体相关的Trainsition Intensity和Transition Color。
因此Wild-NeRF的MLP网络结构如下图所示:

其中 X Y Z XYZ XYZ和 θ ϕ \theta\phi θϕ为原始NeRF的输入, l ( a ) l^{(a)} l(a)为新增的Lantent Appearance Modeling部分,其实就是针对每一张图片输入一个长度的 N N N维的向量来描述该图片的光照条件,而 l ( τ ) l^{(\tau)} l(τ)则是另外一个 N N N维的向量来描述该图片Transition部分的情况。 l ( a ) l^{(a)} l(a)和 l ( τ ) l^{(\tau)} l(τ)都属于Generative Latent Code技术中的Latent Code。
从图中我们可以看到,除了增加 l ( a ) l^{(a)} l(a)和 l ( τ ) l^{(\tau)} l(τ),网络还多输出了Transition Color σ i ( τ ) ( t ) \sigma_{i}^{(\tau)}(t) σi(τ)(t)和Transition Intensity c i ( τ ) ( t ) \mathbf{c}_{i}^{(\tau)}(t) ci(τ)(t)以及一个用于描述不确定度的量 β \beta β, σ i ( τ ) ( t ) \sigma_{i}^{(\tau)}(t) σi(τ)(t)和 c i ( τ ) ( t ) \mathbf{c}_{i}^{(\tau)}(t) ci(τ)(t)参与颜色积分,如下所示: C ^ i ( r ) = ∑ k = 1 K T i ( t k ) ( α ( σ ( t k ) δ k ) c i ( t k ) + α ( σ i ( τ ) ( t k ) δ k ) c i ( τ ) ( t k ) ) \hat{\mathbf{C}}_{i}(\mathbf{r})=\sum_{k=1}^{K} T_{i}\left(t_{k}\right)\left(\alpha\left(\sigma\left(t_{k}\right) \delta_{k}\right) \mathbf{c}_{i}\left(t_{k}\right)+\alpha\left(\sigma_{i}^{(\tau)}\left(t_{k}\right) \delta_{k}\right) \mathbf{c}_{i}^{(\tau)}\left(t_{k}\right)\right) C^i(r)=k=1∑KTi(tk)(α(σ(tk)δk)ci(tk)+α(σi(τ)(tk)δk)ci(τ)(tk)) where T i ( t k ) = exp ( − ∑ k ′ = 1 k − 1 ( σ ( t k ′ ) + σ i ( τ ) ( t k ′ ) ) δ k ′ ) \text { where } T_{i}\left(t_{k}\right)=\exp \left(-\sum_{k^{\prime}=1}^{k-1}\left(\sigma\left(t_{k^{\prime}}\right)+\sigma_{i}^{(\tau)}\left(t_{k^{\prime}}\right)\right) \delta_{k^{\prime}}\right) where Ti(tk)=exp(−k′=1∑k−1(σ(tk′)+σi(τ)(tk′))δk′)
β \beta β积分后得到 β i \beta_i βi, β i \beta_i βi在损失函数中扮演的角色如下所示: L i ( r ) = ∥ C i ( r ) − C ^ i ( r ) ∥ 2 2 2 β i ( r ) 2 + log β i ( r ) 2 2 + λ u K ∑ k = 1 K σ i ( τ ) ( t k ) L_{i}(\mathbf{r})=\frac{\left\|\mathbf{C}_{i}(\mathbf{r})-\hat{\mathbf{C}}_{i}(\mathbf{r})\right\|_{2}^{2}}{2 \beta_{i}(\mathbf{r})^{2}}+\frac{\log \beta_{i}(\mathbf{r})^{2}}{2}+\frac{\lambda_{u}}{K} \sum_{k=1}^{K} \sigma_{i}^{(\tau)}\left(t_{k}\right) Li(r)=2βi(r)2∥∥∥Ci(r)−C^i(r)∥∥∥22+2logβi(r)2+Kλuk=1∑Kσi(τ)(tk)
β i \beta_i βi越大说明该像素不确定度越高,该像素有更多可能来自于Transition的物体,因此权重也越小,具体过程如下图所示:

基于以上操作,Wild-NeRF就可以对室外场景进行一个效果不错的建模,基于 l ( a ) l^{(a)} l(a)还有一个很有意思的应用,即输入不同的 l ( a ) l^{(a)} l(a),网络也会对应渲染出不同光照条件下的场景,看起来非常炫酷,如下图所示:

3. Mip-NeRF
Mip-NeRF原论文名为《Mip-NeRF: A Multiscale Representation for Anti-Aliasing Neural Radiance Fields》,其实在我写这篇博客不久前,又有一篇名为Mip-NeRF 360的论文出炉,效果更为惊艳。Mip-NeRF解决的主要是当训练图片和渲染图片处于不同分辨率条件下时会导致模糊或者错误的问题。
我们知道,原始的NeRF是通过穿过图像像素的一条射线进行积分,在射线上采样的是一个一个的点,而Mip-NeRF则是将这样一条射线更换成了一个圆锥(Cone),如下图所示:
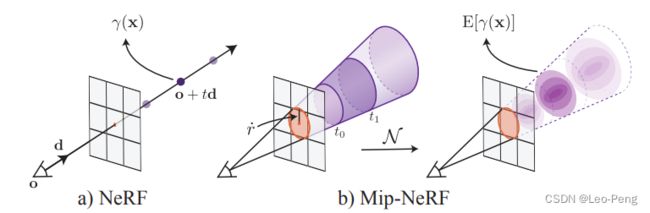
论文里主要说明了在使用圆锥进行采样的情况下如何进行Positional Encoding,首先论文定义了在上图中 [ t 0 , t 1 ] [t_0, t_1] [t0,t1]范围内通过圆锥获得的采样点 x \mathbf{x} x的特征集合: F ( x , o , d , r ˙ , t 0 , t 1 ) = 1 { ( t 0 < d T ( x − o ) ∥ d ∥ 2 2 < t 1 ) ∧ ( d T ( x − o ) ∥ d ∥ 2 ∥ x − o ∥ 2 > 1 1 + ( r ˙ / ∥ d ∥ 2 ) 2 ) } \mathrm{F}\left(\mathbf{x}, \mathbf{o}, \mathbf{d}, \dot{r}, t_{0}, t_{1}\right)=\mathbb{1}\left\{\left(t_{0}<\frac{\mathbf{d}^{\mathrm{T}}(\mathbf{x}-\mathbf{o})}{\|\mathbf{d}\|_{2}^{2}}
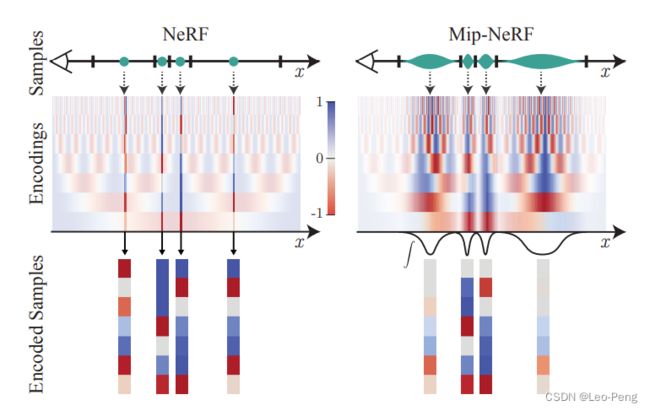
由于Position Encoding对所有的采样点都使用的同样的处理方式,因此在高频部分容易产生混淆,如上左图所示,无论高频低频经过Positional Encoding后输出高频部分有很多相似的蓝色,而Integrated Positional Encoding则可以避免这一问题,对于相对低频的输入经过Integrated Positional Encoding后输出高频部分趋近于0,也就是上右图中的白色,因此就避免了高频混淆。这也就是Mip-NeRF效果好的原因,如下对比图所示:
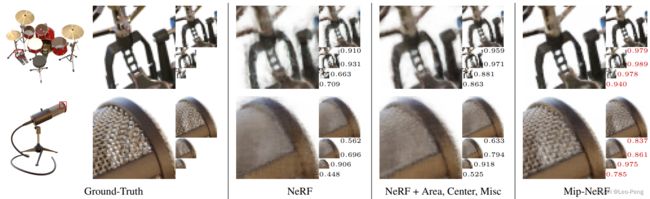
关于Mip-NeRF的积分过程,原论文的补充材料中有我就不在此赘述。Mip-NeRF通过建立高斯分布解决实际问题感觉很棒。
4. BARF
BARF原论文名为《BARF: Bundle-Adjusting Neural Radiance Fields》,该论文解决的问题的主要是原始NeRF对于准确的先验位姿态的依赖,在BARF的实验中,即使没有非常准确的位姿仍然可以取得非常不错的结果。与这项任务相关的论文还有NeRF–,INeRF等等,但是BARF论文中对反向传播的推导是最详细的。
BARF先从2D问题入手,给定如下图(a)中一些Crop图像,要求算法实现对齐并最终恢复到图(c )的结果

最基本的方式是最小化两幅图像之间的光度误差: min p ∑ x ∥ I 1 ( W ( x ; p ) ) − I 2 ( x ) ∥ 2 2 \min _{\mathbf{p}} \sum_{\mathbf{x}}\left\|\mathcal{I}_{1}(\mathcal{W}(\mathbf{x} ; \mathbf{p}))-\mathcal{I}_{2}(\mathbf{x})\right\|_{2}^{2} pminx∑∥I1(W(x;p))−I2(x)∥22其中, x ∈ R 2 \mathbf{x} \in \mathbb{R}^{2} x∈R2为图像坐标, I : R 2 → R 3 \mathcal{I}: \mathbb{R}^{2} \rightarrow \mathbb{R}^{3} I:R2→R3为三通道图像, W : R 2 → R 2 \mathcal{W}: \mathbb{R}^{2} \rightarrow \mathbb{R}^{2} W:R2→R2为通过参数 p ∈ R P \mathbf{p} \in \mathbb{R}^{P} p∈RP描述的一个变换函数,按照梯度下降法的步骤,我们需要求解 Δ p \Delta \mathbf{p} Δp进行迭代,那么 Δ p = − A ( x ; p ) ∑ x J ( x ; p ) ⊤ ( I 1 ( W ( x ; p ) ) − I 2 ( x ) ) \Delta \mathbf{p}=-\mathbf{A}(\mathbf{x} ; \mathbf{p}) \sum_{\mathbf{x}} \mathbf{J}(\mathbf{x} ; \mathbf{p})^{\top}\left(\mathcal{I}_{1}(\mathcal{W}(\mathbf{x} ; \mathbf{p}))-\mathcal{I}_{2}(\mathbf{x})\right) Δp=−A(x;p)x∑J(x;p)⊤(I1(W(x;p))−I2(x))矩阵 A \mathbf{A} A有SLAM基础的同学应该知道,如果是高斯牛顿法就是 A ( x ; p ) = ( ∑ x J ( x ; p ) ⊤ J ( x ; p ) ) − 1 \mathbf{A}(\mathbf{x} ; \mathbf{p})=\left(\sum_{\mathbf{x}} \mathbf{J}(\mathbf{x} ; \mathbf{p})^{\top} \mathbf{J}(\mathbf{x} ; \mathbf{p})\right)^{-1} A(x;p)=(∑xJ(x;p)⊤J(x;p))−1,如果是最速梯度下降法则是 − 1 -1 −1,而其中 J ∈ R 3 × P \mathbf{J} \in \mathbb{R}^{3 \times P} J∈R3×P为雅可比矩阵: J ( x ; p ) = ∂ I 1 ( W ( x ; p ) ) ∂ W ( x ; p ) ∂ W ( x ; p ) ∂ p \mathbf{J}(\mathbf{x} ; \mathbf{p})=\frac{\partial \mathcal{I}_{1}(\mathcal{W}(\mathbf{x} ; \mathbf{p}))}{\partial \mathcal{W}(\mathbf{x} ; \mathbf{p})} \frac{\partial \mathcal{W}(\mathbf{x} ; \mathbf{p})}{\partial \mathbf{p}} J(x;p)=∂W(x;p)∂I1(W(x;p))∂p∂W(x;p)其中 ∂ W ( x ; p ) ∂ p ∈ R 2 × P \frac{\partial \mathcal{W}(\mathbf{x} ; \mathbf{p})}{\partial \mathbf{p}} \in \mathbb{R}^{2 \times P} ∂p∂W(x;p)∈R2×P为变换函数相对参数的导数,这个只要函数预先定义好,导数是好求的。而 ∂ I ( x ) ∂ x ∈ R 3 × 2 \frac{\partial \mathcal{I}(\mathbf{x})}{\partial \mathbf{x}} \in \mathbb{R}^{3 \times 2} ∂x∂I(x)∈R3×2是图像像素值相对空间坐标的导数,由于图像通常是一个高频复杂信号,想求解该导数是非常困难的,于是作者借助网络来解决该问题,将光度误差公式修改如下: min p , Θ ∑ x ( ∥ f ( x ; Θ ) − I 1 ( x ) ∥ 2 2 + ∥ f ( W ( x ; p ) ; Θ ) − I 2 ( x ) ∥ 2 2 ) \min _{\mathbf{p}, \boldsymbol{\Theta}} \sum_{\mathbf{x}}\left(\left\|f(\mathbf{x} ; \mathbf{\Theta})-\mathcal{I}_{1}(\mathbf{x})\right\|_{2}^{2}\right.\left.+\left\|f(\mathcal{W}(\mathbf{x} ; \mathbf{p}) ; \mathbf{\Theta})-\mathcal{I}_{2}(\mathbf{x})\right\|_{2}^{2}\right) p,Θminx∑(∥f(x;Θ)−I1(x)∥22+∥f(W(x;p);Θ)−I2(x)∥22)在求解变换函数 p \mathbf{p} p的同时求解网络参数 Θ \boldsymbol{\Theta} Θ,这样就将上面复杂的数值求解简化成了网络训练过程的梯度下降 ∂ f ( x ) ∂ x \frac{\partial f(\mathbf{x})}{\partial \mathbf{x}} ∂x∂f(x)。我们来重新观察一下这个网络 f f f的作用,输入一个坐标 x \mathbf{x} x,输出是该坐标的像素值,这不正是NeRF完成的工作吗?区别只是NeRF是在三维空间中完成此任务,因此我们定一个三维刚体变换 W : R 3 → R 3 \mathcal{W}: \mathbb{R}^{3} \rightarrow \mathbb{R}^{3} W:R3→R3,NeRF的积分公式可以写为: I ^ ( u ; p ) = g ( f ( W ( ( z 1 u ‾ ; p ) ; Θ ) , … , f ( W ( z N u ‾ ; p ) ; Θ ) ) \hat{\mathcal{I}}(\mathbf{u} ; \mathbf{p})=g\left(f\left(\mathcal{W}\left((z_{1} \overline{\mathbf{u}} ; \mathbf{p}\right) ; \boldsymbol{\Theta}\right), \ldots, f\left(\mathcal{W}\left(z_{N} \overline{\mathbf{u}} ; \mathbf{p}\right) ; \boldsymbol{\Theta}\right)\right) I^(u;p)=g(f(W((z1u;p);Θ),…,f(W(zNu;p);Θ))其中 u ‾ \overline{\mathbf{u}} u为积分向量, z i z_{i} zi为采样点, g ( ⋅ ) g(·) g(⋅)为积分公式, p \mathbf{p} p为三维变换参数,最终损失函数为: min p 1 , … , p M , Θ ∑ i = 1 M ∑ u ∥ I ^ ( u ; p i , Θ ) − I i ( u ) ∥ 2 2 \min _{\mathbf{p}_{1}, \ldots, \mathbf{p}_{M}, \boldsymbol{\Theta}} \sum_{i=1}^{M} \sum_{\mathbf{u}}\left\|\hat{\mathcal{I}}\left(\mathbf{u} ; \mathbf{p}_{i}, \boldsymbol{\Theta}\right)-\mathcal{I}_{i}(\mathbf{u})\right\|_{2}^{2} p1,…,pM,Θmini=1∑Mu∑∥∥∥I^(u;pi,Θ)−Ii(u)∥∥∥22经过上面一通复杂的操作,最后的结论其实就是将表示位姿参数 p 1 , … , p M \mathbf{p}_{1}, \ldots, \mathbf{p}_{M} p1,…,pM作为变量给到网络进行更新。我们知道,在NeRF的输入过程中会有一个Positional Encoding操作,如下所示: γ ( x ) = [ x , γ 0 ( x ) , γ 1 ( x ) , … , γ L − 1 ( x ) ] ∈ R 3 + 6 L \gamma(\mathbf{x})=\left[\mathbf{x}, \gamma_{0}(\mathbf{x}), \gamma_{1}(\mathbf{x}), \ldots, \gamma_{L-1}(\mathbf{x})\right] \in \mathbb{R}^{3+6 L} γ(x)=[x,γ0(x),γ1(x),…,γL−1(x)]∈R3+6L γ k ( x ) = [ cos ( 2 k π x ) , sin ( 2 k π x ) ] ∈ R 6 \gamma_{k}(\mathbf{x})=\left[\cos \left(2^{k} \pi \mathbf{x}\right), \sin \left(2^{k} \pi \mathbf{x}\right)\right] \in \mathbb{R}^{6} γk(x)=[cos(2kπx),sin(2kπx)]∈R6当我们对Positional Encoding操作进行求导后: ∂ γ k ( x ) ∂ x = 2 k π ⋅ [ − sin ( 2 k π x ) , cos ( 2 k π x ) ] \frac{\partial \gamma_{k}(\mathbf{x})}{\partial \mathbf{x}}=2^{k} \pi \cdot\left[-\sin \left(2^{k} \pi \mathbf{x}\right), \cos \left(2^{k} \pi \mathbf{x}\right)\right] ∂x∂γk(x)=2kπ⋅[−sin(2kπx),cos(2kπx)]我们发现,第 k k k次频的Positional Encoding操作会对原本的梯度信号放大 2 k π 2^{k} \pi 2kπ倍,而不同频次之间的梯度又会相互影响,这使得有效地更新 Δ p \Delta \mathbf{p} Δp变得更加困难,为了解决这个问题,作者提出了一个类似于动态低频滤波器的操作,如下所示,对第 k k k次频的Positional Encoding进行加权 γ k ( x ; α ) = w k ( α ) ⋅ [ cos ( 2 k π x ) , sin ( 2 k π x ) ] \gamma_{k}(\mathbf{x} ; \alpha)=w_{k}(\alpha) \cdot\left[\cos \left(2^{k} \pi \mathbf{x}\right), \sin \left(2^{k} \pi \mathbf{x}\right)\right] γk(x;α)=wk(α)⋅[cos(2kπx),sin(2kπx)]其中权重 w k w_{k} wk定义为: w k ( α ) = { 0 if α < k 1 − cos ( ( α − k ) π ) 2 if 0 ≤ α − k < 1 1 if α − k ≥ 1 w_{k}(\alpha)= \begin{cases}0 & \text { if } \alpha
5. NSVF
NSVF原论文名为《Neural Sparse Voxel Fields》,该论文解决的是要是原始NeRF训练过程收敛速度慢的问题。原始NeRF是使用一个MLP网络的参数对整个空间进行建模,即原始NeRF的MLP网络的输入只有采样点的坐标和方向,输出就是该采样点的颜色和密度,因此我们可以理解为所有的信息都保存在MLP网络中。而NSVF是使用一个Sparse Voxel Octree来辅助对空间建模,具体说来就是NSVF通过Sparse Voxel Octree保存了空间中各个节点位置的Feature,然后根据采样点的位置对Feature进行插值,最终输入MLP网络的是采样点的Feature和方向,因此空间中的信息一部分保存在了MLP网络中,另一部分则保存在Sparse Voxel Octree的Feature中。
NSVF的网络结构如下图所示:
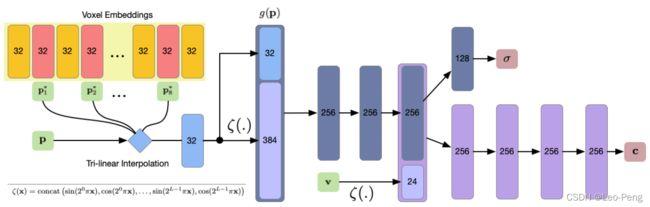
其中,Voxel Embedding部分即为Sparse Voxel Octree保存的特征,每个Voxel有8个角点 p 1 ∗ … p 8 ∗ p_1^*\ldots p_8^* p1∗…p8∗,每个角点存储着 d d d维的特征 g ~ i ( p 1 ∗ ) , … , g ~ i ( p 8 ∗ ) ∈ R d \widetilde{g}_{i}\left(\boldsymbol{p}_{1}^{*}\right), \ldots, \tilde{g}_{i}\left(\boldsymbol{p}_{8}^{*}\right) \in \mathbb{R}^{d} g i(p1∗),…,g~i(p8∗)∈Rd,记为,根据采样点 p p p 落在Voxel中的位置对Voxel的8个特征按照距离进行插值得到采样点对应的特征,然后对该Feature进行Positional Embedding操作: g i ( p ) = ζ ( χ ( g ~ i ( p 1 ∗ ) , … , g ~ i ( p 8 ∗ ) ) ) g_{i}(\boldsymbol{p})=\zeta\left(\chi\left(\widetilde{g}_{i}\left(\boldsymbol{p}_{1}^{*}\right), \ldots, \widetilde{g}_{i}\left(\boldsymbol{p}_{8}^{*}\right)\right)\right) gi(p)=ζ(χ(g i(p1∗),…,g i(p8∗)))其中 χ ( . ) \chi(.) χ(.)表示插值操作, ζ ( . ) \zeta(.) ζ(.)表示Position Embedding操作。采样点方向 v \mathbf{v} v同样进行Position Embedding操作后同 g i ( p ) g_{i}(\boldsymbol{p}) gi(p)一起输入MLP网络,并最终输出颜色 c \boldsymbol{c} c和密度 σ \boldsymbol{\sigma} σ。
文中提到,原始的NeRF可以视为NSVF的一个特例: g i ( p ) = ζ ( χ ( p 1 ∗ , … , p 8 ∗ ) ) = ζ ( p ) g_{i}(\boldsymbol{p})=\zeta\left(\chi\left(\boldsymbol{p}_{1}^{*}, \ldots, \boldsymbol{p}_{8}^{*}\right)\right)=\zeta(\boldsymbol{p}) gi(p)=ζ(χ(p1∗,…,p8∗))=ζ(p)基本操作都是相同的,只是没有Voxel用于保存特征而已。
除了网路基本的结构外,文章还提出了Self-Pruning和Progressive Training两个方法,其中Self-Pruning即在训练过程,对于删除密度较小的栅格,以起到减小计算量的作用;Progressive Training则是在训练过程中不断减小Voxel的尺寸,以达到提高精度的目的。如下图就是Progressive Training的过程:
6. Semantic-NeRF
Semantic-NeRF原论文名为《In-Place Scene Labelling and Understanding with Implicit Scene Representation》,该论文的主要贡献时在NeRF的基础上加入了语义的结果,论文方法并不复杂,就是在MLP网络上加了一路Semantic的输出,然后仿照颜色的积分方式对Semantic进行积分,如下图所示:
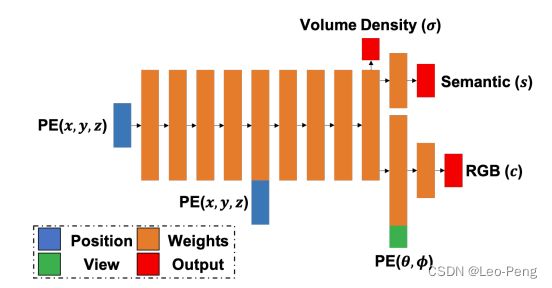
在我看来,Semantic-NeRF并没有什么物理模型支撑和数学证明过程,仅仅是利用了网络的插值的作用,该论文展示了这样一个应用,对于一个场景通过极少数视角/像素的语义标注,就可以将其他视角/像素的语义标注推导出来,在该作者后面的论文中有将其衍生出一个标注工具,感兴趣的读者可以自行去查阅论文。
以上就完成了这几篇论文的一个小结,基于原始NeRF优化的论文还有很多,而且最近也不断有新的论文发表,相信在不久的将来该方法会应用到各项工程技术中,有问题欢迎交流~