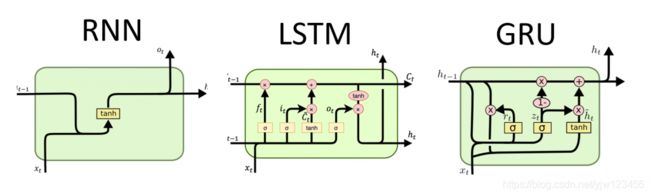
从RNN到LSTM再到GRU
引言
RNN
循环神经网络是处理时序数据的,它将序列按照顺序分成了很多时间步。在每个时间步,它的输入依赖于前一个时间步的输出(记忆单元)和当前的输入信息。废话不多说,直接上图,上公式。本文其实相当于一个整理,如何想看详细的介绍,建议看最后参考处的文章。
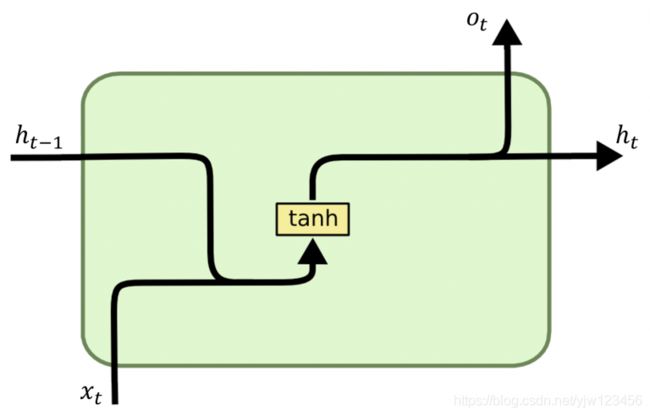
其中 x t x_t xt表示当前的输入, h t − 1 h_{t-1} ht−1表示前一个时刻的隐藏状态,初始为0向量。
o t o_t ot是当前时刻的输出, h t h_t ht是当前时刻的隐藏状态。
首选来看 h t h_t ht的计算:
h t = tanh ( W h h h t − 1 + W h x x t + b h ) (1) h_t = \tanh(W_{hh} h_{t-1} + W_{hx} x_t + b_h) \tag{1} ht=tanh(Whhht−1+Whxxt+bh)(1)
即计算当前时刻隐藏状态的时候,同时考虑了输入 x t x_t xt和前一个时刻隐藏状态 h t − 1 h_{t-1} ht−1的信息。
为了更好的说明,假设 W h h W_{hh} Whh的大小是 ( 100 × 100 ) (100 \times 100) (100×100), W h x W_{hx} Whx的大小是 ( 100 × 10000 ) (100 \times 10000) (100×10000),隐藏状态 h t − 1 h_{t-1} ht−1的大小 ( 100 × 1 ) (100 \times 1) (100×1),输入 x t x_t xt的大小 ( 10000 × 1 ) (10000 \times 1) (10000×1),最后偏差 b h b_h bh的大小 ( 100 × 1 ) (100 \times1) (100×1)。
h t ⏟ 100,1 = tanh ( W h h ⏟ 100 ,100 ⋅ h t − 1 ⏟ 100,1 + W h x ⏟ 100,10000 ⋅ x t ⏟ 10000,1 + b h ⏟ 100,1 ) \underbrace{h_t}_\text{100,1} = \tanh( \underbrace{W_{hh}} _\text{100 ,100} \cdot \underbrace{h_{t-1}}_\text{100,1} + \underbrace{W_{hx}}_\text{100,10000} \cdot \underbrace{x_t}_\text{10000,1} + \underbrace{b_h}_\text{100,1}) 100,1 ht=tanh(100 ,100 Whh⋅100,1 ht−1+100,10000 Whx⋅10000,1 xt+100,1 bh)
现在要做的事情是把上面这个公式描述简化,以便于理解和记忆。
把 W h h W_{hh} Whh和 W h x W_{hx} Whx按列叠加起来得 W h ( 100 × 10100 ) W_h(100 \times 10100) Wh(100×10100):
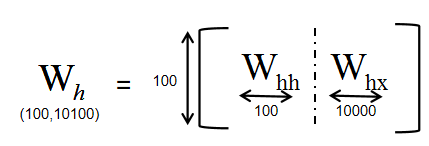
把 h t − 1 h_{t-1} ht−1和 x t x_t xt按行叠加起来得 [ h t − 1 , x t ] ( 10100 × 1 ) [h_{t-1},x_t](10100 \times 1) [ht−1,xt](10100×1):
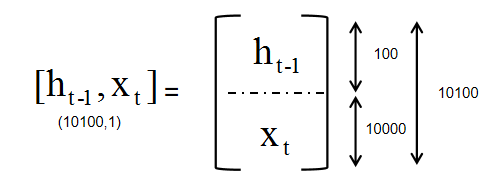
这样,公式 ( 1 ) (1) (1)就可以写成:
h t = tanh ( W h [ h t − 1 , x t ] + b h ) (2) h_t = \tanh(W_h [h_{t-1},x_t] + b_h) \tag{2} ht=tanh(Wh[ht−1,xt]+bh)(2)
本文后面也会一直按照这种写法来简化。
得到了 h t h_t ht之后,就可以计算 o t o_t ot:
o t = g ( W o h t + b o ) (3) o_t = g(W_o h_t + b_o) \tag{3} ot=g(Woht+bo)(3)
这里的 g g g是激活函数,根据任务的不同可以用sigmoid或softmax。
RNN虽好,但是存在梯度消失和梯度爆炸的问题,导致一旦序列过长,在反向传播时RNN就会出问题。
其中梯度爆炸问题,有一个解决方法是梯度修剪(gradient clipping),就是设定一个阈值,当梯度向量超过某个阈值时,将它减少到阈值。而梯度消失问题更难解决。因此有人提出了GRU来解决这个问题。
LSTM
LSTM是RNN的变种,是为了解决RNN存在的长期依赖问题而专门设计出来的。所谓长期依赖问题是,后面的单词在很长的时间序列后还依赖前面的单词,但由于梯度消失问题,导致前面的单词无法影响到后面的单词。
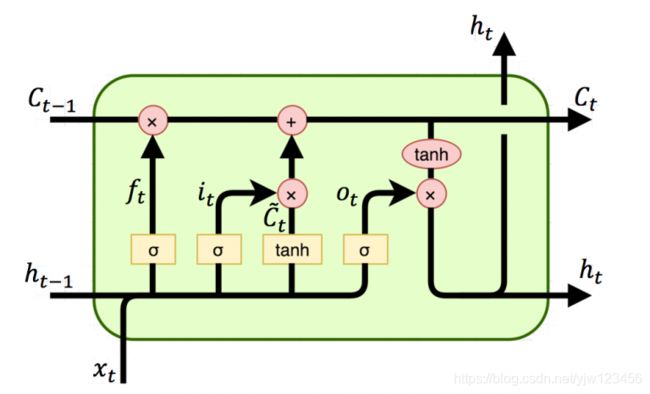
x t x_t xt是当前时刻的输入, h t − 1 h_{t-1} ht−1是上一个时刻的隐藏状态, C t − 1 C_{t-1} Ct−1是上一时刻的单元状态。 h t h_t ht是当前时刻的隐藏状态, C t C_t Ct是当前时刻的单元状态(记忆)。
相当于是LSTM会有两个输出。
其中输出 h t h_t ht是与当前的单元状态 C t C_t Ct有关的,而 C t C_t Ct是由前一时刻的单元状态 C t − 1 C_{t-1} Ct−1和候选值 C ∼ t \overset{\sim}{C}_t C∼t有关的。 因此我们先来看下候选值 C ∼ t \overset{\sim}{C}_t C∼t的计算公式:
C ∼ t = tanh ( W c [ h t − 1 , x t ] + b c ) (4) \overset{\sim}{C}_t = \tanh(W_c [h_{t-1},x_t] + b_c) \tag{4} C∼t=tanh(Wc[ht−1,xt]+bc)(4)
这里的候选值和RNN的隐藏状态计算方法类似。当前单元状态受两个门控制,分别是遗忘门 f t f_t ft和输入门 i t i_t it。
遗忘门:
f t = σ ( W f [ h t − 1 , x t ] + b f ) (5) f_t = \sigma(W_f [h_{t-1},x_t] + b_f) \tag{5} ft=σ(Wf[ht−1,xt]+bf)(5)
使用sigmoid函数使得门的取值限定为[0,1]之间。
输入门:
i t = σ ( W i [ h t − 1 , x t ] + b i ) (6) i_t = \sigma(W_i [h_{t-1},x_t] + b_i) \tag{6} it=σ(Wi[ht−1,xt]+bi)(6)
其中,遗忘门用来控制内存中之前的单元状态 C t − 1 C_{t-1} Ct−1是否会被遗忘掉,输入门决定候选值(哪些维度)能多大程度的存入当前单元状态 C t C_t Ct:
C t = f t ∗ C t − 1 + i t ∗ C t ∼ (7) C_t = f_t * C_{t-1} + i_t * \overset{\sim}{C_t} \tag{7} Ct=ft∗Ct−1+it∗Ct∼(7)
基于当前单元状态 C t C_t Ct,就可以得到当前时刻的隐藏状态 h t h_t ht:
h t = o t ∗ tanh ( C t ) (8) h_t = o_t * \tanh (C_t) \tag{8} ht=ot∗tanh(Ct)(8)
其中 o t o_t ot是输出门,不难猜到,输出门也是由 h t − 1 , x t h_{t-1},x_t ht−1,xt计算而来的:
o t = σ ( W o [ h t − 1 , x t ] + b o ) (9) o_t = \sigma(W_o [h_{t-1},x_t] + b_o) \tag{9} ot=σ(Wo[ht−1,xt]+bo)(9)
输出门控制了当前时刻能输出多少隐藏状态。
基于当前的隐藏状态,可以计算出当前时刻的输出 y ^ t \hat y_t y^t:
y ^ t = s o f t m a x ( W y h t + b y ) (10) \hat y_t = softmax(W_y h_t + b_y) \tag{10} y^t=softmax(Wyht+by)(10)
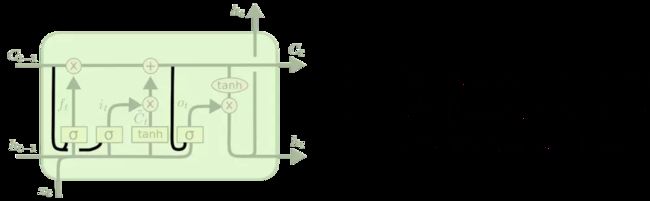
Peephole LSTM
具有窥视孔连接的LSTM
GRU
GRU 旨在解决RNN 中出现的梯度消失问题。GRU也可以被视为LSTM的变体,启发于LSTM,但更易于实现和计算,且在某些情况能产生同样出色的结果。
GRU把遗忘门和输入门合并成为一个“更新门”,把单元状态和隐藏状态合并,还有其他变化。这样做使得 GRU比标准的LSTM模型更简单。
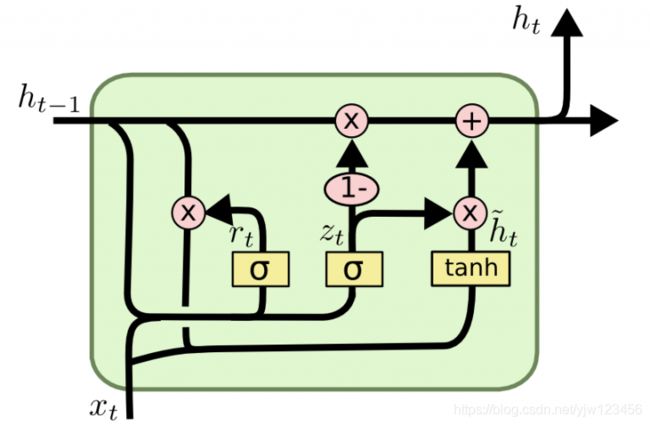
x t x_t xt是当前时刻的输入, h t − 1 h_{t-1} ht−1是上一个时刻的隐藏状态, h t h_t ht是当前时刻计算出来的隐藏状态。
在计算当前时刻的隐藏状态时,它会首先计算一个候选状态 h ∼ t \overset{\sim}{h}_t h∼t,而在计算候选状态时,会考虑重置门的取值。
所以先来看重置门 r t r_t rt是如何计算的:
r t = σ ( W r [ h t − 1 , x t ] ) (11) r_t = \sigma(W_r [h_{t-1},x_t]) \tag{11} rt=σ(Wr[ht−1,xt])(11)
使用sigmoid函数使得门的取值限定为[0,1]之间。
一般这里可以不用考虑偏置,原论文中也没有偏置。
如果重置门近于0,当前候选值 h ∼ t \overset{\sim}{h}_t h∼t会忽略前一个隐藏状态 h t − 1 h_{t-1} ht−1,并用当前的输入 x t x_t xt来计算。这可以有效地让隐藏状态抛弃任何将来发现的不相关信息。 来看一下候选值的计算公式:
h ∼ t = tanh ( W h [ r t ∗ h t − 1 , x t ] ) (12) \overset{\sim}{h}_t = \tanh(W_h [r_t * h_{t-1},x_t]) \tag{12} h∼t=tanh(Wh[rt∗ht−1,xt])(12)
可以看到,和RNN隐藏状态计算类似,不过多了一个重置门,重置门的大小和 h t − 1 h_{t-1} ht−1是一致的,*代表逐元素相乘。
计算出来候选值之后,通过更新门来控制前一个隐藏状态有多少信息可以传递到当前隐藏状态。这类似于LSTM的记忆单元,可以让GRU记住长期信息。
来看一下更新门的计算公式:
z t = σ ( W z [ h t − 1 , x t ] ) (13) z_t = \sigma(W_z [h_{t-1},x_t]) \tag{13} zt=σ(Wz[ht−1,xt])(13)
门的计算方法类似,不过权重矩阵不同。最后就可以计算当前时刻的隐藏状态了:
h t = ( 1 − z t ) ∗ h t − 1 + z t ∗ h ∼ t (14) h_t = (1-z_t) * h_{t-1} + z_t * \overset{\sim}{h}_t \tag{14} ht=(1−zt)∗ht−1+zt∗h∼t(14)
因为每个隐藏单元都是独立的重置门和更新门,所以每个隐藏单元将学习捕获到不同时间范围的依赖。这些学习捕获短期依赖的单元倾向于使重置门频繁地激活,但学习长期依赖的单元几乎总是激活更新门。
总结
LSTM和GRU都能通过各种门将重要信息保留,保证其在长期传播的时候也不会被丢失。
GRU和LSTM的性能在很多任务上不分伯仲。
GRU有两个门,而LSTM有三个门,因此GRU计算速度更快。
数据集小时倾向于使用GRU,但是数据集很大的情况下,LSTM性能更好。
参考
- 吴恩达深度学习——循环神经网络
- Learning Phrase Representations using RNN Encoder–Decoder for Statistical Machine Translation翻译
- RNN, LSTM & GRU
- LSTM背后的数学原理
- 从零实现循环神经网络