Deconvolution layer或者Transposed convolution layer的理解

这个是github上关于反卷积的一些动态示意图

一文读懂卷积反卷积，博主的对反卷积的理解，主要来自这篇文章

下面，主要结合上面的第二个链接，来理解Deconvolution layer 看它是怎么进行计算的。

同时附上 pytorch 库里面关于这个layer 参数的介绍：

参考这个链接看pytorch

 

其实在实际应用的时候，convTranspose2d主要是前面（in channel, out channel, kernel size, stride, padding, outpadding）

所以接下来就是怎么理解反卷积里面的这些参数，主要结合上面第二个博客里的内容； 首先，你把convTranspose2d当作是conv2d的反过来的过程。

对于conv2d 我们有 (inchannel, outchannel, kernel size, stride, padding) 这些参数

（kernel size： k； stride： s； padding， p）

假设现在我们的input是 （n, inchannel, i, i） i 是input的size大小，n 是input这个batch的大小， inchannel 是channel的个数

那么经过了刚才的那个卷积： output的size o可以表示为：

      

那么现在我们假设上式是完全可以整除的，我们现在经历了卷积；接下来我们想通过反卷积再从o 恢复到 i：

我们推导下 o 到 i 的公式：

既然我们想把反卷积看成类似于卷积的操作；我们试图把第二个公式恢复成 类似于第一个公式那种 新的输入size 新的padding大小 新的kernel size  新的stride 的样子

结合着反卷积动态图，我们知道在反卷积的时候， = 1 因为看起来是在新的input上面 紧挨着滑动的。（动图可以看我文章最开头附着的链接）

我们接着，就按着想把 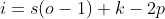 变形为新的 卷积操作的公式进行变形（注意反卷机的时候，kernel size 跟卷积的时候一样，大小不变）

那么对于transpose2d ，如果把它当作一个新的卷积的话：

我们用i1 p1 s1 k1 代表新的参数：

 其实这个新的input结合图像也很好理解，就是那个output 然后有（o-1 个间隙）每个间隙插入（stride - 1）个0； 所以最终input 大小就变成了这个和的形式

k1 = k

s1 = 1

那么原来的公式   

就变形为： 

后面就是通过将o 变形成这样的。具体每一个新的参数是什么表达式前面已经给出了。

也就是说，这里完全可以把 卷积 与 反卷积看成一个可以逆过来的过程。

那么我们现在给一个例子来说明下反卷积怎么来看这个过程

例如，deconvolution layer 的kernel size， stride， padding， outpadding依次是（ 9 ，4，3，1）outpadding是在已经计算之后再加一圈, 假设反卷机层的 input size 表示为 input

那么可以看成一个新的卷积操作，新的卷积操作的各项参数是： 

i_new = i + (i -1)(stride - 1)  = i + (i -1) * 3 ;   padding_new = k-1-padding = 9 - 1 - 3 = 5;

stride_new  = 1; kernel_size = 9

那么output = (i_new + 2 * padding_new - kernel_size) / stride + 1 = (4i - 3 + 2 * 5 - 9)/1 + 1 = 4i - 2 + 1 = 4i - 1;

所以为了让这个卷积之后如果是4的整数倍的话，需要 outpadding  = 1 

如果你自己不想像我这样既推导，也计算（方便自己理解）；

你可以直接记忆公式即可。  （因为这个是之前用逆回来的公式推导的，这里的o是反卷积层的input ； s  反卷积层的stride ；k 反卷机层的kernel； p 反卷积层的 padding）

继续给一个例子 （9 4 4 3）kernel size， stride， padding， outpadding依次是（ 9 4 4 3）

这个反卷积层看作一个新的卷积层，假设反卷积层的 input size 表示为 input

新的input size 是 input + (input - 1)(stride - 1) = input + (input -1 )* 3

new_padding = k-1 - padding = 9-1-4 = 4

new_kernel = kernel = 9

new_stride = 1

所以输出 output可以看作这个新的卷积的输出： input + (input -1 )* 3 + 2 * 4 - 9 + 1 = 4*input-3

所以这个反卷积中 为了最后是4的整数倍， outpadding = 3