图像特征的学习笔记

• 图像都有哪些特征？
  1、颜色特征
  是一种全局特征，描述了图像或图像区域所对应的景物的表面性质。是基于像素点的特征，由于颜色对图像或图像区域的方向、大小等变化不敏感，所以颜色特征不能很好地捕捉图像中对象的局部特征。颜色直方图是最常用的表达颜色特征的方法，其优点是不受图像旋转和平移变化的影响，进一步借助归一化还可不受图像尺度变化的影响，但是缺少颜色空间分布的信息。
  2、纹理特征
  也是一种全局特征，也描述了景物的表面性质，反映的是图像中同质现象的视觉特征，体现物体表面的具有缓慢变换或周期性变化的表面组织结构排列属性。图像纹理通过像素及其周围空间邻域的灰度分布来表现，即局部纹理信息。局部纹理信息不同程度上的重复性，就是全局纹理信息。
  3、形状特征
  形状通常与图像中的特定目标对象有关，是人们对目标的最初认识，有一定的语义信息，是比颜色特征和纹理特征更高一层的特征。一个好的形状描述符应具备独特性、完备性、几何不变性、灵活性以及抽象性。以对图像中物体或区域的分割为基础，两种经典的算法是SIFT和HOG。
  4、空间关系特征
  所谓空间关系，是指图像中分割出来的多个目标之间的相互的空间位置或相对方向关系。通常空间位置信息可以分为两类：相对空间位置信息和绝对空间位置信息。前一种关系强调的是目标之间的相对情况，如上下左右关系等，后一种关系强调的是目标之间的距离大小以及方位。空间关系特征可加强对图像内容的描述区分能力，但它常对图像或目标的旋转、反转、尺度变化等比较敏感。

• 各个特征都有什么描述方法？
  1、颜色特征描述方法：
  a)颜色直方图
  适用于描述难以自动分割的图像和不需要考虑物体空间位置的图像，表达了不同颜色在图像中所占的比例，以反映图像颜色的组成分布，即各种颜色出现的概率。不会受到图像旋转、平移、尺度等影响，但是无法描述图像中的某个具体对象和物体，图像中颜色的局部分布以及各种色彩的空间位置无法描述。会出现一对多的情况，就是颜色占比很一致，但实际表达的高层语义完全不同。
  b)颜色矩
  c)颜色集
  d)颜色聚合向量
  e)颜色相关图
  其他详细方法可参见颜色特征(颜色直方图，颜色矩，颜色集，颜色聚合向量和颜色相关图)
  2、纹理特征描述方法：
  纹理方法分为4类：基于统计数据、基于结构、基于模型、信号处理。
  构成纹理特征的两个要素：纹理基元、由基元排列得到的纹理
  纹理分析过程：从像素出发；检测出纹理基元；获得有关基元排列分布方式的信息；建立纹理基元模型。总的来说就是通过一定的图像处理技术提取出纹理特征参数,从而获得纹理的定量或定性描述的处理过程。
  a)灰度共生矩阵(Gray-level Co-occurrence Matrix, GLCM)
  定义1： 灰度共生矩阵（Gray Level Co-occurrence Matrix，GLCM）统计了灰度图中像素间的灰度值分布规律以区分不同的纹理。灰度共生矩阵中每个元素的值可以定义为(x, y)点与(x + dx, y + dy)点的值对为(i, j)的概率。统计整幅图像中每一种灰度值组合出现的概率矩阵 P 即为灰度共生矩阵（前半句还能看懂，后半句呵呵）。
  理解：
  A.“灰度”：由此可知材料原始数据是一幅灰度图或者至少他是一个单频段的图片，就是如下面的左图 $I$。右图就是GLCM矩阵，看到有8行8列，这是因为左边的像素值最大就到8。实际上右面就是左面任意两个像素点（1到8）任意组合得到的。比如说GLCM(1,1)表示左面两个点的组合就是$I$(1)和$I$(1)；GLCM(1,2)表示左面两个点的组合就是$I$(1)和$I$(2)。图里的箭头指向很清楚，可以看到GLCM不同位置实际就是左面灰度矩阵中有几对，那就是几。比如GLCM(1,1)就只有1对，GLCM(1,2)有2对，GLCM(1,3)左面没有就是0。
  
  B.“共生”：纸面意思可知是一种对应相邻关系。所以呢应该就是指上面说的这个像素对。那么怎么定义的共生呢（成对）？规则就是定义一个（a,b）,那么位于（x,y）和（x+a,y+b）的两个点是一对。所以a,b实际就是两个点的相隔单位。如下图：
  
  a=1,b=0 ，这个时候就是水平成对，0度扫描（红色）
  a=1,b=1，这个时候就是右对角成对，45度扫描（黄色）
  a=0,b=1，这个时候就是垂直成对，90度扫描（蓝色）
  a=-1,b=-1，这个时候就是左对角成对，135度扫描（绿色）
  C.“矩阵”：这个矩阵是一个概率矩阵，用两个位置的像素的联合概率密度来定义的。对上面我们得到的GLCM进行归一化就可以得到出现概率矩阵了。
  综上： 距离差分值（a，b） 取不同的数值组合，可以得到不同情况下的联合概率矩阵。（a，b）取值要根据纹理周期分布的特性来选择，对于较细的纹理，选取（1，0）、（1，1）、（2，0）等小的差分值。所以，一幅图象的灰度共生矩阵能反映出图象灰度关于方向、相邻间隔、变化幅度的综合信息，它是分析图象的局部模式和它们排列规则的基础。
  特别注意： 由于一幅灰度影像的灰度级一般为256级，假设图像为512*512。那么共生矩阵就要计算$256^2\ast 512\ast 512$次计算，那就太多了。所以一般在计算前将灰度值再次量化，设置为8或者16级，这样只会颜色变淡，但不影响纹理特征的提取。
  而且，灰度共生矩阵维度大，一般不作为区分纹理的特征，基于它构建的一些 统计量 才会作为纹理分类的特征。比如：能量，熵，对比度，均匀性，相关性，方差，和平均，和方差、和熵、差方差、差平均、差熵、相关信息测度以及最大相关系数。
  python代码实现：

#拒绝重复造车，直接使用skimage来进行计算
import skimage
#from skimage.feature import graycomatrix, graycoprops
import numpy as np
#以图片引入的array为源数据，计算灰度共生矩阵，生成GLCM
skimage.feature.graycomatrix(image, distances, angles, levels=None, symmetric=False, normed=False)
#计算GLCM的纹理属性,以归一化的GLCM为数据源
skimage.feature.graycoprops(P, prop='contrast')
#包含6个统计量contrast对比度、dissimilarity非均匀性、
#homogeneity均匀性、ASM角二阶矩、energy能量、correlation相关性
#*****************************skimage中的例子*********************************
import matplotlib.pyplot as plt
from skimage.feature import graycomatrix, graycoprops
from skimage import data
PATCH_SIZE = 21
#打开图片数据
image = data.camera()
# 从图像的草地区域选择一些点作为草地的试验块
grass_locations = [(280, 454), (342, 223), (444, 192), (455, 455)]
grass_patches = []
for loc in grass_locations:
    grass_patches.append(image[loc[0]:loc[0] + PATCH_SIZE,
                               loc[1]:loc[1] + PATCH_SIZE])
# 从图像的草地区域选择一些点作为草地的试验块
sky_locations = [(38, 34), (139, 28), (37, 437), (145, 379)]
sky_patches = []
for loc in sky_locations:
    sky_patches.append(image[loc[0]:loc[0] + PATCH_SIZE,
                             loc[1]:loc[1] + PATCH_SIZE])
# 计算每个块的GLCM矩阵，并从中提取非均匀性和相关性统计值
xs = []
ys = []
for patch in (grass_patches + sky_patches):
    glcm = graycomatrix(patch, distances=[5], angles=[0], levels=256,
                        symmetric=True, normed=True)#计算GLCM矩阵
    xs.append(graycoprops(glcm, 'dissimilarity')[0, 0])#计算非均匀性
    ys.append(graycoprops(glcm, 'correlation')[0, 0])#计算相关性
# 画图
fig = plt.figure(figsize=(8, 8))#创建一个大的图布
# display original image with locations of patches
ax = fig.add_subplot(3, 2, 1)#三行两列图里的第一个图为原图以及提取的点位置
ax.imshow(image, cmap=plt.cm.gray,
          vmin=0, vmax=255)
for (y, x) in grass_locations:
    ax.plot(x + PATCH_SIZE / 2, y + PATCH_SIZE / 2, 'gs')
for (y, x) in sky_locations:
    ax.plot(x + PATCH_SIZE / 2, y + PATCH_SIZE / 2, 'bs')
ax.set_xlabel('Original Image')
ax.set_xticks([])
ax.set_yticks([])
ax.axis('image')

# 对于每个块的两个属性（非均匀，相关）作为x,y画为散点图
ax = fig.add_subplot(3, 2, 2)
ax.plot(xs[:len(grass_patches)], ys[:len(grass_patches)], 'go',
        label='Grass')
ax.plot(xs[len(grass_patches):], ys[len(grass_patches):], 'bo',
        label='Sky')
ax.set_xlabel('GLCM Dissimilarity')
ax.set_ylabel('GLCM Correlation')
ax.legend()

# 展示各个图像块的实际样子
for i, patch in enumerate(grass_patches):
    ax = fig.add_subplot(3, len(grass_patches), len(grass_patches)*1 + i + 1)
    ax.imshow(patch, cmap=plt.cm.gray,
              vmin=0, vmax=255)
    ax.set_xlabel('Grass %d' % (i + 1))

for i, patch in enumerate(sky_patches):
    ax = fig.add_subplot(3, len(sky_patches), len(sky_patches)*2 + i + 1)
    ax.imshow(patch, cmap=plt.cm.gray,
              vmin=0, vmax=255)
    ax.set_xlabel('Sky %d' % (i + 1))

# 绘制图形
fig.suptitle('Grey level co-occurrence matrix features', fontsize=14, y=1.05)
plt.tight_layout()
plt.show()

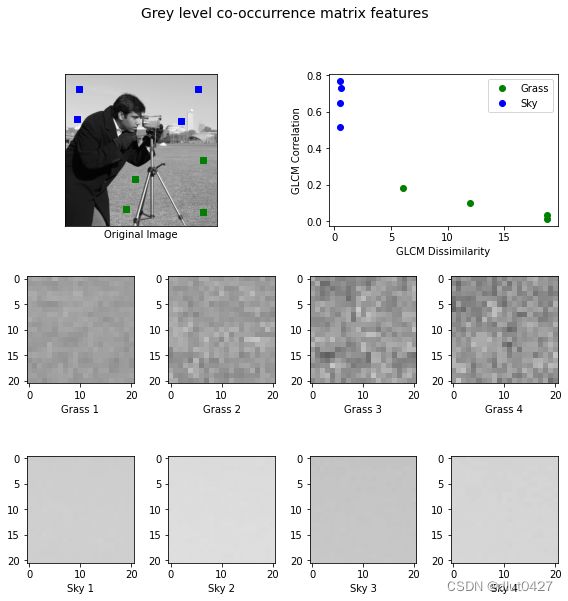
结果如下图：

b) LBP特征(Local Binary Pattern)
LBP（Local Binary Pattern，局部二值模式）是一种用来描述图像局部纹理特征的算子；它具有旋转不变性和灰度不变性等显著的优点。

原始的LBP算子定义为在33的窗口内，以窗口中心像素为阈值，将相邻的8个像素的灰度值与其进行比较，若周围像素值大于中心像素值，则该像素点的位置被标记为1，否则为0。这样，33邻域内的8个点经比较可产生8位二进制数（通常转换为十进制数即LBP码，共256种），就可以得到该窗口中心像素点的LBP值，利用该值来反映该区域的纹理信息。
参考：目标检测的图像特征提取之（二）LBP特征
c）其他详细见数字图像处理—图像纹理特征
3、形状特征描述方法：
有待继续丰富。。。。
参考：
1.图像特征(三)——纹理特征(GLCM、LBP)
2.灰度共生矩阵的原理及实现(特征提取)-OpenCV
3.scikit-image Documentation