模型压缩——重参数化

模型压缩主要的方法有：重参数化、剪枝、量化等，本章主要讲重参数化
在解决恒等映射时对卷积核插值或者重新生成一个卷积核时有些会直接使用Dirac初始化增加的权重。
Dirac初始化看这里：https://www.e-learn.cn/topic/1523429

重参数化

重参数化有并行合并和串行合并(主要是为了合并模块成一个卷积)，要想合成只有一条，那要先串行再并行，而且串行合并的那一块不能有ReLU，sigmoid、tanh这种公式只有一种的可以，ReLU为在x>0和x<0的公式不同所以不行。
优点：训练时采用多分支的网络使模型获取更好的特征表达，测试时将并行融合成串行，从而降低计算量和参数量，提升速度(融合后理论上和融合前识别效果一样，实际基本都是稍微降低一点点)

RepVGG 和ACNe的重参数化方法

ACNet

在add中：$w1\cdot x+w_2\cdot x=(w_1+w_2)\cdot x$

在这里，1x3 Conv等于第二行和第三行权值为0的3x3 Conv，3x1 Conv等于第二列和第三列权值为0的3x3 Conv。
那么，此时图中的3个尺寸不同Conv就可以等价于3个尺寸都相同的卷积了，也就可以应用上面add的公式了。
实际上Conv后会后BN，BN和Conv的融合看底下的RepVGG

RepVGG

RepVGG和ACNet很像，主要概念的在训练的时候采用原来多分支的复杂网络，在测试的使用将多分支合并成一条支路进行测试，不再训练，从而提升速度。(并行和并，对支路是有限制的，如下图这样的支路，每一条支路可以先合并成一个卷积，然后再支路合并)


RepVGG的重参数化过程：

1. 将所有的Conv和BN合并，参数融合公式：$w_{i,:,:,:}^{\prime }=\frac{{\gamma }_i}{{\sigma }_i}{w}_{i,:,:,:},b_i^{\prime }=-\frac{{\mu }_i{\gamma }_i}{{\sigma }_i}+{\beta }_i$，其中$w_i$为原卷积权重，${\mu }_i$、${\sigma }_i$、${\gamma }_i$和${\beta }_i$分别为BN的均值、方差、尺度因子和偏移因子。
2. 将融合后的Conv转为3×3 Conv(尺度最大的Conv)。1×1 Conv转换成3×3 Conv采用中心权值与1×1 Conv相等，四周权值为0的方法。恒等映射采用第i核Conv的第i通道下的中间权值为1，其余为0的3×3 Conv替换。(其它尺度的Conv同理)
3. 合并分支的中所有3×3 Conv。将所有分支的卷积核的权值w和偏置b相加，形成一个新的3×3 Conv(上面的ACNet)。

推导：
上面的过程中第二步和第三步很简单，但第三步只能在分支最后连接采用add的方法，聚合连接不行。主要是第一步的推导，这里将推导这一过程。
Conv中每一次计算的公式可以表达成：$Conv(x)=w\cdot x$(一般不加bias，加bias同理)
BN的公式是：$BN(x)={\gamma }_i\cdot (\frac{x-{\mu }_i}{\sqrt{{\sigma }_i^2+ϵ}})+{\beta }_i$，$ϵ$极小值
那么Conv+BN的公式为${\gamma }_i\cdot (\frac{w\cdot x-{\mu }_i}{\sqrt{{\sigma }_i^2+ϵ}})+{\beta }_i=\frac{{\gamma }_i}{\sqrt{{\sigma }_i^2+ϵ}}{w}_i\cdot x-\frac{{\gamma }_i{\mu }_i}{\sqrt{{\sigma }_i^2+ϵ}}+{\beta }_i$
由于$ϵ$是极小值，可以忽略，那么就成了$\frac{{\gamma }_i}{{\sigma }_i}{w}_i\cdot x-\frac{{\gamma }_i{\mu }_i}{{\sigma }_i}+{\beta }_i$ ，此时就是新的卷积：$Conv(x)=w^{\prime }\cdot x+{\beta }^{\prime }$,$w_{i,:,:,:}^{\prime }=\frac{{\gamma }_i}{{\sigma }_i}{w}_{i,:,:,:},b_i^{\prime }=-\frac{{\mu }_i{\gamma }_i}{{\sigma }_i}+{\beta }_i$
因此忽略了$ϵ$，以及权重融合时计算机的精度问题，会导致测试的时候出现实际效果略微下降。

Diverse Branch Block (DBB)

从上图可以看到DBB涉及到串联和并联的融合，其中上面的RepVGG和ACNet已经解释了并联融合，这里主要讲解串联融合。
上面也写了BN和Conv融合，这里不讲

串联1x1 Conv和KxK Conv融合

这里是将串联1x1 Conv和KxK Con卷积融合。
DBB里提出的融合方法为先将1x1 Conv的0维和1维对换(0维为核数，1维为通道数)，然后再用它对KxK Conv进行Conv操作得出合并后的Conv核的权值，最后再用合并后的Conv核对Input进行Conv操作，如下图。
公式：$X⨂F1⨂F2=X⨂(F2⨂trans(F1))$

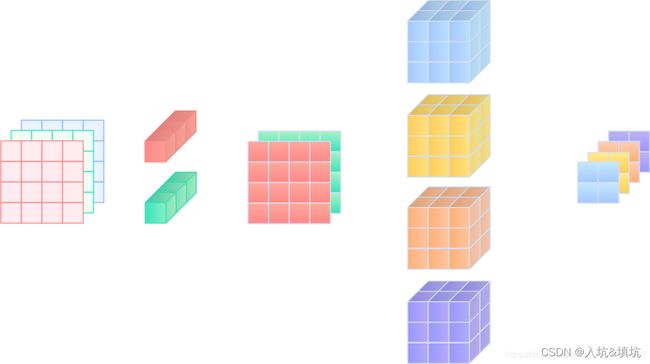
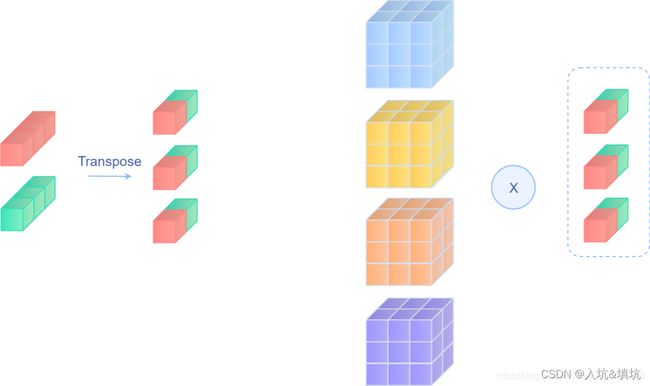
假设输入为CxHxW，1x1 Conv有M个，则1x1 Conv$\in R^{M\times C\times 1\times 1}$，输出为MxHxW，KxK Conv有N个，则KxK Conv$\in R^{N\times M\times K\times K}$，输出为NxHxW
对换1x1 Conv的0维度和一维度后，1x1 Conv$\in R^{C\times M\times 1\times 1}$，就成了C个通道数为M的1x1 Conv，此时再对KxK Conv进行Conv，输出就为KxK Conv$\in R^{N\times C\times K\times K}$

1x1 Conv和AVG(Average Pooling)融合

AVG等价于N核Conv(假设输入特征图由N张)，低i核在第i通道下的所有权值为$\frac{1}{siz{e}^2}$，其余通道下的权值为0，此时融合1x1 Conv和AVG=融合1x1 Conv和KxK Conv，回到了上面的串联1x1 Conv和KxK Conv融合

拼接融合

当每条支路都变成采用一个KxK Conv实现，然后Concat所有支路的输出，就等价于采用一个在通道上拼接所有支路Conv权值的KxK Conv。

RMNet

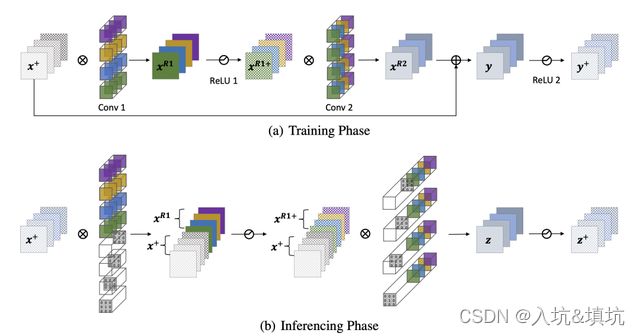
RMNet基于ResNet实现的，如果block里存在ReLU的话block的最后一定要有，只有这样才能保证下一个block接收到的输入都是正的（线性映射）。而对于像MobileNet2这种网络，它的ReLU操作是放置在Block中间，此时无法保证下一个Block的输入一定是正的。所以此时不能直接做ReLU操作，而是使用一个PReLU(LeakReLU)，对输入的特征将PReLU的alpha参数设置为1，以保持线性映射。而对于卷积后的特征，将PReLU的alpha参数设置为0，此时等价于ReLU。

去残差，不存在下采样

如上图，残差连接重点是2个block，融合方法如下：
已知输入为正值，特征通道为N，Block里的第一个Conv后存在ReLu，第二个Conv后会和Block的输入进行add，再ReLU。

Step1: 对第一个Block里的第一层Conv进行插值，先插入N个Conv核，插入的第i个Conv核的第i个通道下的中间权值为1，四周为0。现在第一个Conv输出的特征图就相比原来多出了N张，这N张组成的特征和Block输入的一样。由于Block输入为正值，插值的Conv的权重只有0和1，所有即便再经过ReLU，输出的也和原来一样(多出来的N张中的第i张就等于Block输入特征的第i张)。
Step2: 对Block中的第二层Conv进行插值。第二层Conv的每个核多增加N个通道，第i个核的多增加的第i个通道的中间值为1，其余为0。（第i核输出的是第i张特征图，原本进行Res的时候适合Block输入的第i张特征图进行add，此时Block输入的第i张特征图变成了上一层Conv输出的多增加的第i张特征图，那么第二层Conv的每个Conv核对应于这张的卷积核通道就是第i个多增加的通道）

去残差，下采样

有两种，第一种如下：

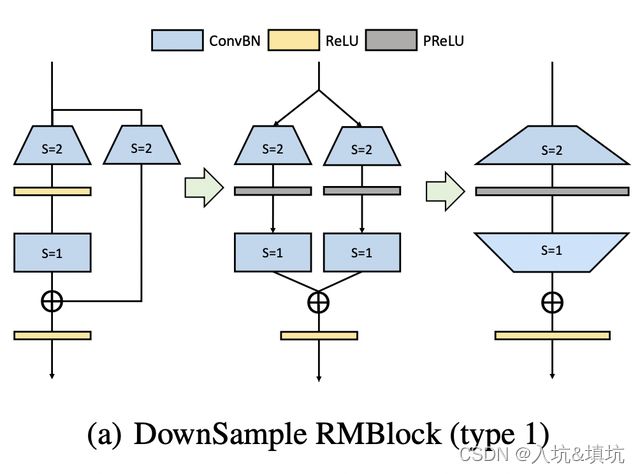
将旁路分支中 stride=2 的1x1卷积经过pad补0填充为3x3卷积，扩张通道数(这个卷积原本就是扩通道)。
此时卷积出来的结果有正有负（跟前面讨论的Mobilenetv2的情况类似），为了保证恒等映射，我们这里采用的是PReLU(残差分支即左边的，alpha权重为0等价于ReLU，旁路分支的alpha权重为1，等价于恒等映射)。
然后我们再接入一个Dirac初始化的3x3卷积来保证恒等映射。最后我们能融合成最右边图的情况。

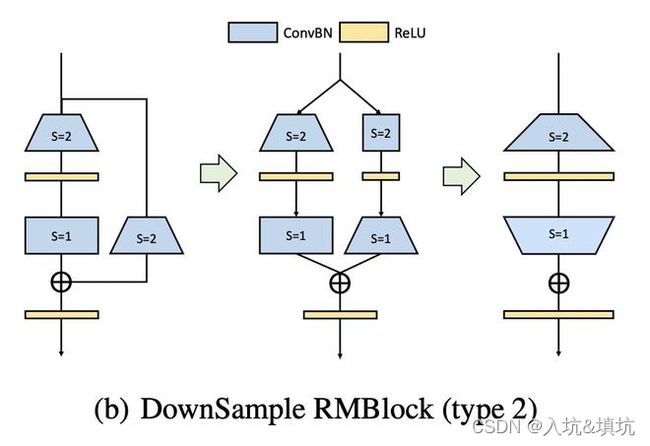
第二种：先采用大小3x3， stride=2 的恒等映射卷积，降低分辨率。再用 stride=1 的3x3卷积扩张通道数。
两种的融合方法：两条支路的第一层卷积在个数这个维度上拼接，假如左边m核Conv，右边n核Conv，拼接后就是m+n核的Conv。底下两个s=1的Conv就在通道上拼接。（无论先扩通道还是后扩，第一层右边的Conv影响的是核的个数，不关Conv核的通道数，所以上面的拼接没问题。而原本的1x1 Conv s=2在第二种里就成了1x1 Conv s=1了，最后又使用padding将其变成3x3的Conv，然后再来和左边第二层的Conv进行通道拼接）
从参数量角度的话，第二种比较少

• 方案1: Conv1(C4C33) + PReLU(4C) + Conv2(4C2C33) = 108C^2 + 4C(两方案的HW可以抵消，所以只算C，C为输入Block输入特征的通道，4C代表扩充的通道，原本左右两侧第一层各自扩充2C，合并后就成了4C)
• 方案2: Conv1(C3C33) + Conv2(3C2C33) = 81C^2（左侧扩充2C，右侧不扩充，所以Conv1共扩充了3C，实际最后输出了2C）