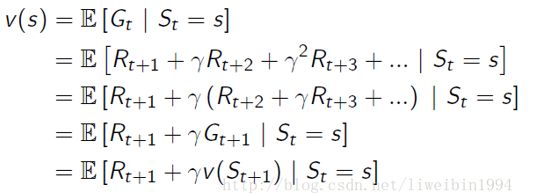一文搞定！！！多智能体强化学习的前世今生

        最近在学习多智能体的强化学习，看了几篇高质量基础论文，发现还是很有必要将强化学习的体系简单过一遍，然后再有针对性地练习代码。

推进文章：多智能体强化学习路线图 (MARL Roadmap)

转载总结链接：从0开始强化学习——强化学习的简介和分类 

                        多智能体强化学习笔记 01

                        马尔科夫决策过程

                                              

1.强化学习简介

1.1 强化学习概念

        强化学习与监督学习、非监督学习都属于机器学习，是人工智能的范畴。值得一提的是深度学习也是机器学习的一种范式，深度学习在机器学习的基础上优化了数据分析，建模过程的流程也缩短了，由神经网络统一了原来机器学习中百花齐放的算法，减少了特征工程的构成，同时调参工作也变得更加复杂。深度学习针对数据量较多，硬件GPU配置较高，特征维数较复杂的系统，传统的机器学习反之。

 

       强化学习（Reinforcement Learning,RL）是用来描述和解决智能体（agent）在与环境的交互过程中通过学习策略以达成回报最大化或实现特定目标的问题，它是一种决定下一步行动方案的机器学习任务，通过试错学习（trial and error learning）来实现这一目标，努力使reward回报最大化。强化学习并不需要具体的标签，而是通过与环境不断的反馈、交互，学习到适合环境的决策方案。

1.2 强化学习分类

 1.2.1 理解环境模型（Model Based RL）与不理解环境模型（Model Free RL）

        不理解环境的RL就是仅仅通过环境的反馈，来影响决策，不会对环境建模，也没有想象能力。

        理解环境的RL是会根据真实的环境构造出一个虚拟环境，不仅可以根据真实环境的反馈指引决策，也可以在虚拟环境中的反馈指导决策。

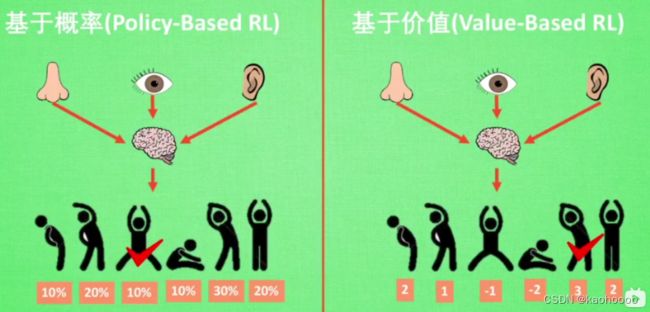
1.2.2 基于概率（Policy Based RL）和基于价值（Value-Based RL）

        基于概率的RL是对每一种行为都会计算出一个概率，然后根据概率去决定采取哪种行为，这种方法中，概率值小的行为也有可能被选中，主要针对连续类动作。

        而基于价值的RL是对每种行为计算出一个价值，对于动作的决策完全取决于价值的大小，价值最大的动作就会被选中，主要针对离散类动作。

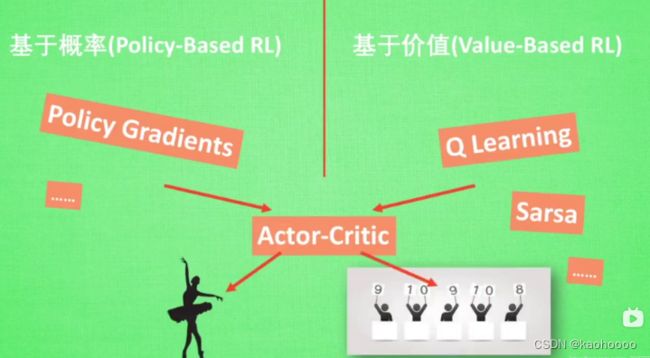
         也存在将policy-based RL和 value-based RL结合的方法：Actor-Critic，其中Actor部分就是通过基于概率的方法做出动作决策，Critic部分可以基于做出的动作给出动作的价值评判。这样就实现了在policy gradients基础上增加价值学习的过程。

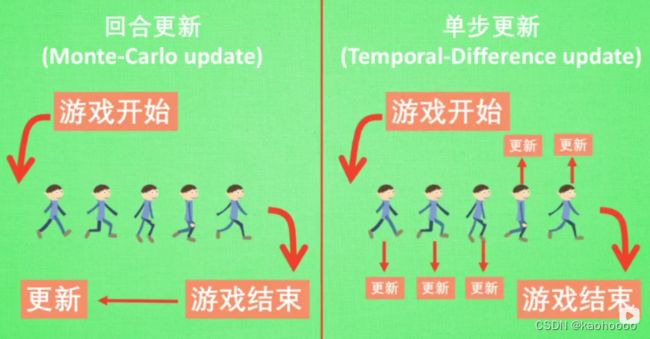
 1.2.3 回合更新（Monte-Carlo update，蒙特卡洛）和单步更新（Temporal-Difference update，TD）

        回合更新是指某种游戏整个回合结束才对RL参数进行更新，而单步更新是指在每一次决策之后就进行更新。

         目前大多数方法都是基于单步更新的，因为单步更新更有效率，并且许多问题并不属于回合问题。常见的基于回合更新的方法有：Policy Gradients、Monte-Carlo Learning；单步更新方法：Q Learning、Sarsa、升级版的Policy Gradients

1.2.4 在线学习（online learning）和离线学习（offline learning）

        在线学习是指本人参加游戏，边学边玩。离线学习是指通过学习自己以前的游戏记录或者他人的游戏记录，从中学习经验的方法。常见的在线学习方法有：Sarsa、Sarsa(λ)；离线学习方法有：Q Learning、Deep Q Learning。

2.多智能体强化学习

2.1 基础知识

2.1.1 多智能体强化学习

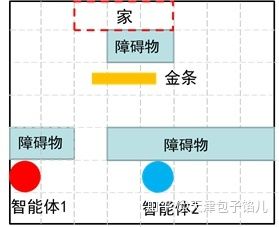
       举一个强化学习的简单例子：如图所示为两个智能体将金条搬运回家的例子。在这里我们称两个智能体分别是小红和小蓝。该例子的故事应该是这样的：小红和小蓝是幸福甜蜜的一对夫妻，有一天他们在离家不远的地方发现一根金条，这根金条需要两个人一人抬着一边才能扛回家。假设他们各自的初始位置如图1所示。要想把金条扛回家，小红和小蓝必须先绕过障碍物，然后每个人到达金条的一边，扛起金条后，两人还得绕开家门口的障碍物，这样才能将金条扛回家。

两个智能体搬运金条

        这是一个典型的多智能体协作的例子。该例子来自于多智能体强化学习综述论文《Multi-agent reinforcement learning: An overview》，这里对原文中的例子稍稍改编了一下。

        从这个例子中，我们可以思考一下，什么是多智能体强化学习。我觉得多智能体强化学习至少应该包括如下几个要素：

（1） 在多智能体系统中至少有两个智能体。

（2） 智能体之间存在着一定的关系，如合作关系（如本例），竞争关系（如多人游戏），或者同时存在竞争与合作的关系。

（3） 每个智能体最终所获得的回报不仅仅与自身的动作有关系，还跟对方的动作有关系。如本例中每个智能体要想获得回报，必须是金条被两个智能体一起搬回家。

 2.1.2 马尔科夫与博弈

        首先，马尔科夫是指多智能体系统的状态符合马尔科夫性，即下一时刻的状态只与当前时刻有关，与前面的时刻没有直接关系。

        其次：博弈描述的是多智能体之间的关系。

（1）马尔科夫决策过程

状态转移矩阵：

        对于一个具体的状态s和它的下一个状态s’ ，它们的状态转移概率(就是从s转移到s’的概率)定义为：

         假如总共有n种状态可以选择。那么状态转移矩阵P定义为：

         矩阵中第 i 行表示：当前状态为 i，那么它的下一个状态为1 , … , n  的概率分别为 ​,...,​。显然这一行所有概率之和为1。

马尔科夫过程：

        是一个二元组 ，其中S为状态集合，P为状态转移概率矩阵。

马尔科夫奖励过程 ：

        简单标示为 >。R表示为从S到S’能够获得的奖励期望，为折扣因子。

奖励之和：

        ​是某个具体的episode所获得的return，当然我们的目标是想找到一个路径使得的值最大，也就是累积奖赏G最大,G表示从s开始一直到终点的所有奖励之和。因为离s越远的地方一般影响较小，所以加了一个折扣因子来表达影响衰减。

Value Function (价值函数) ：

        值函数表示在状态 s 下，​的期望

 Bellman Equation贝尔曼方程：

         贝尔曼方程，由价值函数的定义公式推导而来，可以发现最后为一个递归过程。从最后的推导结果来看，一个状态 s 的价值 V(s) 由两部分组成：一部分是​，它代表即时奖励的期望，它与下一个状态无关，另一个是下一时刻状态的价值期望。

 Markov Decision Process马尔科夫决策过程：

        马尔科夫决策过程是一个五元组，它是在前面马尔科夫奖励过程的基础上添加了**动作集(A)**改进来的。在强化学习的简介中我们也知道，agent与环境是通过执行动作来进行交互的。因此，我们需要添加动作集进来，这样从一个状态转移到另一个状态就是因为执行了动作才会产生的。

 policy策略π：

        策略表示在一个状态s下，agent接下来可能会采取的任意一个action的概率分布。对于每一个状态s都会有这样一个π(a|s)，所有状态的π(a|s)就形成 整体策略π，策略π是指所有状态都要使用这个策略，不是单独指某一个状态。无论怎样，我们的目标是最大化累积奖赏，所以我们可以通过不断地改进我们的策略，使得我们最后能够获得最大累积奖赏。

（2）博弈

        博弈论英文为game theory，从宏观上可以将博弈论研究的问题分为：合作博弈和非合作博弈，现代狭义的博弈论一般指非合作博弈。

        非合作博弈根据参与博弈的参与人做决策的先后顺序可以分为：静态博弈和动态博弈。静态博弈是指参与人同时做决策，常用标准型（normal form）表述其策略。如两人零和博弈等。动态博弈是指参与人有先后顺序做决策，且后者能观察到前者所做的决策，如围棋等。常用扩展型（extensive form）来表述其策略，常用的扩展型表述为博弈树。

        马尔可夫决策过程包含一个智能体与多个状态。矩阵博弈包括多个智能体与一个状态。随机博弈(stochastic game / Markov game)是马尔可夫决策过程与矩阵博弈的结合，具有多个智能体与多个状态，即多智能体强化学习。为更好地理解，引入如下定义：

静态博弈：static/stateless game是指没有状态s，不存在动力学使状态能够转移的博弈。例如一个矩阵博弈。

阶段博弈：stage game，是随机博弈的组成成分，状态s是固定的，相当于一个状态固定的静态博弈，随机博弈中的Q值函数就是该阶段博弈的奖励函数。若干状态的阶段博弈组成一个随机博弈。

重复博弈：智能体重复访问同一个状态的阶段博弈，并且在访问同一个状态的阶段博弈的过程中收集其他智能体的信息与奖励值，并学习更好的Q值函数与策略。

        多智能体强化学习就是一个随机博弈，将每一个状态的阶段博弈的纳什策略组合起来成为一个智能体在动态环境中的策略。并不断与环境交互来更新每一个状态的阶段博弈中的Q值函数（博弈奖励）。

         对于一个随机博弈可以写为，其中n表示智能体数量，S表示状态空间，表示第i个智能体的动作空间，表示状态转移概率，在（0,1）范围内，表示回报值。

        对于一个多智能体强化学习过程，就是找到每一个状态的Nash均衡策略，然后将这些策略联合起来。根据每个智能体的奖励函数可以对随机博弈进行分类。若智能体的奖励函数相同，则称为完全合作博弈或团队博弈。若智能体的奖励函数逆号，则称为完全竞争博弈或零和博弈。

3.多智能体强化学习分类

        多智能体强化学习中的实验环境通常是分为一下几种：完全合作的任务，完全竞争的任务，混合着竞争与合作的任务。

3.1 完全合作的任务

        在完全合作的环境中，agents与环境进行交互与学习，在交互与学习的过程中，agents获得相同的reward信号，即如果它们合作做的很好，那么就告诉给它们正的reward，如果它们并没有合作，或者没有做的比较好的时候，就不给予reward，甚至给予负的reward（cost），更一般地说法：agent具有相同的奖励函数（如果有不同的reward，那么也可以将这些reward相加，那么就可以转化成这样同一个reward的性质了，目的就是最大化全局的reward）。

        所以，在这类的环境中，学习目标当然是：最大化折扣累计回报了。即所有agent一起努力，将大家的reward最大化。因为agent之间的目标并不冲突，所以可以直接地将single agent的算法直接运用过来（注意一下，因为reward函数相同，所以这个思路很直接），那么用过来就会有一个建模的问题：我是应该single agent还是multiagent呢？

        single agent就是将所有agent的action看成一个action的向量，所以这个single agent的学习目标是学习出一个policy能够在每个state下做出相应的action向量，让折扣累积收益最大。

        multiagent的角度呢，就是将每个agent单独拿出来学习，每个agent决定一个action，从集中式的action向量拆分成一个个独立的action。这样的方法就是independent q-learning。

        但是直接independent q-learning会带来一些效率与其他的问题，比如agent直接的action可能会相互影响，导致最终收敛到的policy并不是全局最优的policy。比如：最优的策略是所有agent采用相同的action，一旦有一个action不同就给予很大的惩罚，那么在学习探索的过程中，因为惩罚的存在，agent可能很难学到这个最优的policy，涉及的算法有：JAL，FMQ，Team-Q，Distributed-Q，OAL。

3.2完全竞争的任务

        在完全竞争的环境中，可以很直观地理解为：每个agent都是只关心自己的reward，想要最大化自己的reward，并不考虑自己想要最大化自己的reward的action对于他人的影响。

        一个比较常见的环境就是：两个agent在环境中交互，他们的reward互相为相反数，即 r1=−r2 。在这样的环境中，最大化自己的reward就是最小化对手的reward，所以agent间不能存在合作与竞争的可能，这样的环境很常见，很多双人的棋类的游戏的reward经常就这样进行设计，比如围棋，alphago的目的就是最大化自己的胜率，最小化对手的胜率。

        在这种环境中做planing的话，一种很经典的做法就是冯诺伊曼的minimax的算法，我们可以把这个思想扩展到MARL中agent的学习过程，比如minimax Q-learning：Q1=maxa1mina2Q(s,a1,a2)。

3.3 混合着竞争与合作的任务

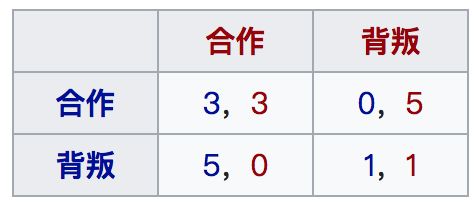
         在这个环境中，agent依然是独立获得自己的reward，但是reward的设计非常有意思，当每个agent只考虑最大化自己的reward时，反而可能会使得自己的reward与另外agent的reward陷入更差的情况。以囚徒困境来讲：

        当agent想要最大化自己的reward时，每个agent都会选择背叛-背叛，因为在这种情况下：当另外的agent选择合作时，我能获得5的reward，比3高；当另外的agent选择竞争时，我能获得1的reward，比0高，这也就是所谓的nash均衡。所以当两个agent都这么考虑的话，最终就是竞争-竞争，agent的reward都是1，但是其实我们观察局面，会发现可能存在一种更好的结果，那就是：合作-合作，这样的话，双方的reward都是3，3比1好，同时两个agent的total reward为6，比任意的情况都好。

        但是很多情况下我们并不知道另外一个agent会是什么类型，环境的reward是什么类型，所以其实学习出Nash均衡的策略在这样的环境中是一种保守的选择，虽然没有合作-合作好，但是确保了自己的reward，从这个角度出发，有：Nash-Q。Nash-Q或许好，但是我们却希望能够在学习中尝试与对手合作，达成合作-合作的局面，如果不可以的话，最终再收敛到竞争-竞争的局面，涉及到的算法：WoLF-IGA，WoLF-PHC，GIGA，GIGA-WoLF，CE-Q等。