关联规则算法(The Apriori algorithm)
一、前言
最近在看 无监督学习 的时候,发现欠缺了数据挖掘的知识,回来补充~
关联规则的目的在于在一个数据集中找出项之间的关系,也称之为购物篮分析 (market basket analysis)。例如,购买鞋的顾客,有10%的可能也会买袜子,60%的买面包的顾客,也会买牛奶。这其中最有名的例子就是"尿布和啤酒"的故事了。
本篇的Apriori算法主要是基于频繁集的关联分析。其主要目的就是为了寻找强关联规则。
二、重要概念
要理解频繁集、强关联规则,要先借助下面的一个情境,来介绍几个重要概念。
下表是一些购买记录:
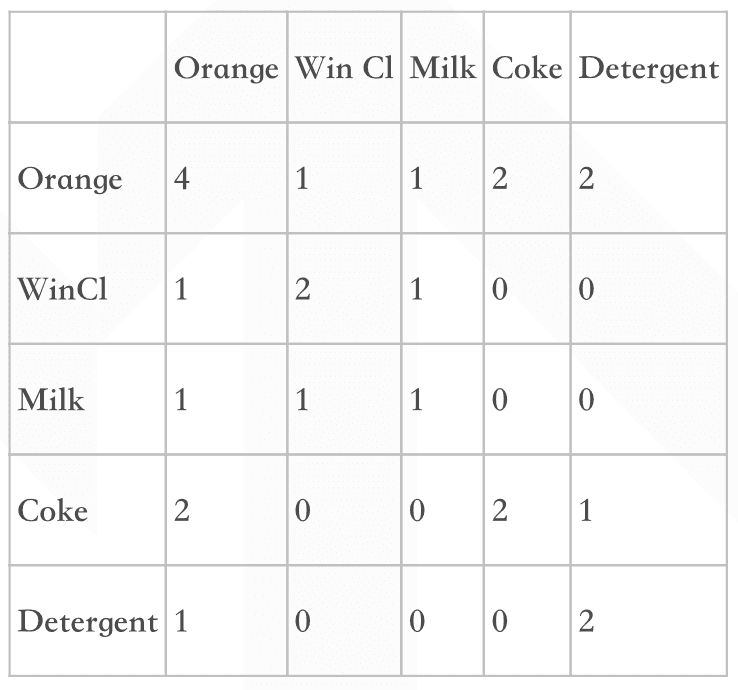
将购买记录整理,可得到下表,横栏和纵栏的数字表示同时购买这两种商品的交易条数。如购买有Orange的交易数为4,而同时购买Orange和Coke的交易数为2。
1. 置信度(Confidence)
置信度,表示这条规则有多大程度上值得可信。
设条件的项的集合为A,结果的集合为B。置信度计算在A中,同时也含有B的概率。即Confidence(A->B)=P(B|A)。例 如计算"如果Orange则Coke"的置信度。由于在含有Orange的4条交易中,仅有2条交易含有Coke。其置信度为0.5。
2. 支持度(Support)
支持度,计算在所有的交易集中,既有A又有B的概率。
例如在5条记录中,既有Orange又有Coke的记录有2条。则此条规则的支持度为2/5=0.4。现在这条规则可表述为,如果一个顾客购买了Orange,则有50%的可能购买Coke。而这样的情况(即买了Orange会再买Coke)会有40%的可能发生。
3. 频繁集
支持度大于预先定好的最小支持度的项集。
4. 关联规则
关联规则:令项集I={i1,i2,...in},且有一个数据集合D,它其中的每一条记录T,都是I的子集。那么关联规则是形如A->B的表达式,A、B均为I的子集,且A与B的交集为空。这条关联规则的支持度:support = P(A并B)。这条关联规则的置信度:confidence = support(A并B)/suport(A)。
强关联规则:如果存在一条关联规则,它的支持度和置信度都大于预先定义好的最小支持度与置信度,我们就称它为强关联规则。
三、算法的原理和过程
下面用一个例子说明算法的过程:
1. 数据准备
项目集合 I={1,2,3,4,5};
事务集 T:
设定最小支持度(minsup)=3/7,最小置信度(misconf)=5/7。
2. 生成频繁项目集
假设:n-频繁项目集为包含n个元素的项目集,例如1-频繁项目集为包含1个元素的项目集
则这里,1-频繁项目集有:{1},{2},{3},{4},{5}
生成2-频繁项目集的过程如下:
首先列出所有可能的2-项目集,如下:
{1,2},{1,3},{1,4},{1,5}
{2,3},{2,4},{2,5}
{3,4},{3,5}
{4,5}
计算它们的支持度,发现只有{1,2},{1,3},{1,4},{2,3},{2,4},{2,5}的支持度 满足要求,因此求得2-频繁项目集:
{1,2},{1,3},{1,4},{2,3},{2,4}
生成3-频繁项目集:
对于现有的2-频繁项目集,两两取并集,并确保第三个二元组也在2-频繁项目集内,把得到的所有3-项目集分别计算支持度,剔除不满足最小支持度的项目集;
例如,
{1,2},{1,3}的并集得到{1,2,3};
{1,2},{1,4}的并集得到{1,2,4};
{1,3},{1,4}的并集得到{1,3,4};
{2,3},{2,4}的并集得到{2,3,4};
但是由于{1,3,4}的子集{3,4}不在2-频繁项目集中,所以需要把{1,3,4}剔除掉。{2,3,4} 同理剔除。
然后再来计算{1,2,3}和{1,2,4}的支持度,发现{1,2,3}的支持度为3/7 ,{1,2,4}的支持度为2/7,所以需要把{1,2,4}剔除。因此得到3-频繁项目集:{1,2,3}。
重复上面步骤继续寻找n-频繁项目集,直到不能发现更大的频繁项目集。所以,到此,频繁项目集生成过程结束。
3. 生成强关联规则
这里只说明3-频繁项目集生成关联规则的过程,即以集合{1,2,3}为例:
回顾事物集,先生成1-后件的关联规则:
(1,2)—>3,置信度=3/4(出现(1,2)的记录共4条,其中有3条包含3,所以3/4);
(1,3)—>2,置信度=3/5;
(2,3)—>1,置信度=3/3;
第二条置信度<5/7,未达到最小置信度,所以剔除掉。所以对于3-频繁项目集生成的强关联规则为:(1,2)—>3和(2,3)—>1。
这表示,如果1、2出现了,则极有可能出现3;2、3出现,则极有可能有1。
四、代码解析
不定期更新