Adaptive Graph Encoder for Attributed Graph Embedding 阅读笔记
我的博客链接
0. 总览
0.1 文章是关于什么的?(what?)
图卷积网络,属性图嵌入,自适应学习,拉布拉斯平滑
0.2 要解决什么问题?(why?|challenge)
已经存在的GCN-based 模型有三个主要缺陷:
- 作者实验显示图卷积网络的滤波器和权重矩阵的纠缠会损害性能和鲁棒性。
- 作者表明在这些方法中的图卷积滤波器是广义拉普拉斯平滑滤波器的特例,但它们并没有保留最佳的低通特性。
- 现有算法的训练目标通常是回复邻接矩阵或特征矩阵,而这些矩阵与现实应用不总是是一致的。
0.3 用什么方法解决?(how?)
作者提出了一个自适应图编码 Adaptive Graph Encoder (AGE)的属性图嵌入框架:
- 为了更好地避免节点特征中的高频噪音,作者首次应用了精心设计的拉普拉斯平滑滤波器。
- AGE采用自适应编码器,该编码器可以迭代地增强滤波后的功能,以实现更好的节点嵌入。
0.4文章有什么创新?
- 上述方法即为创新点。
0.5 效果如何?
AGE超过最好的图嵌入模型在节点聚类和链接预测任务上。
0.6 还存在什么问题?
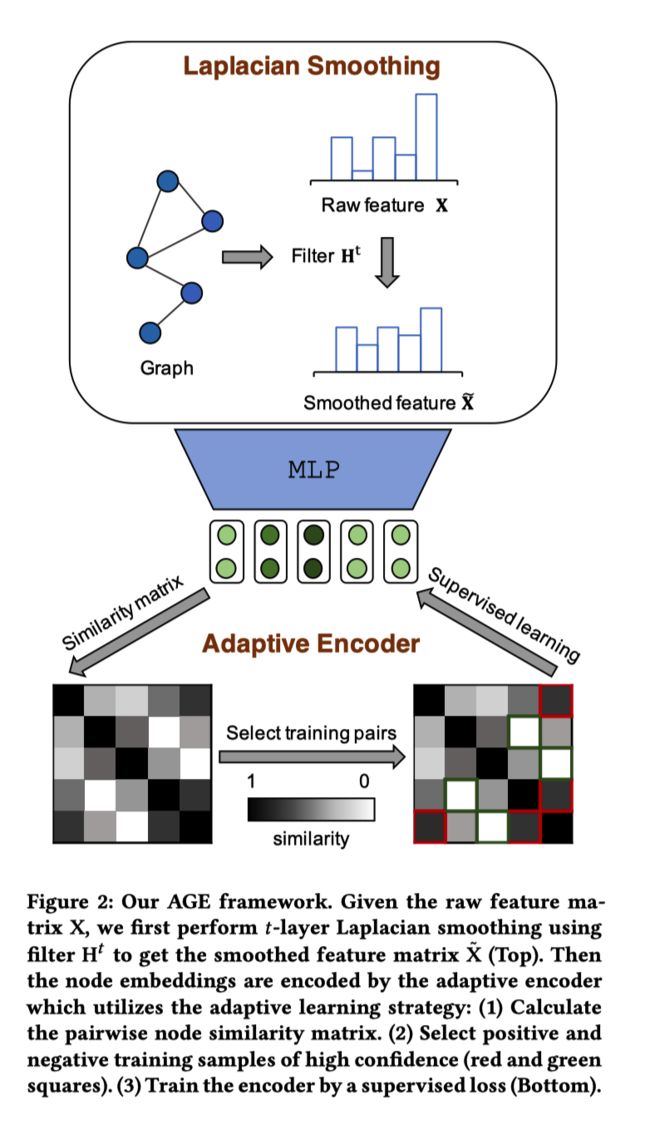
- 拉普拉斯平滑滤波器:设计的滤波器 H \mathbf{H} H用作低通滤波器,以对特征矩阵 X \mathbf{X} X的高频分量进行去噪。平滑后的特征矩阵 X ~ \tilde{\mathbf{X}} X~被用作自适应编码器的输入。
- 自适应编码器:为了获得更具代表性的节点嵌入,该模块通过自适应选择高度相似或不相似的节点对来构建训练集。 然后以监督的方式训练编码器。
2.1 拉普拉斯平滑滤波器
图学习基本假设:图上的邻近节点应该相似,因此,节点特征在图流形上应该是平滑的。
2.1.1 平滑信号
为了衡量信号 x x x的平滑程度,计算图的Rayleigh quotient(瑞利商):
R ( L , x ) = x ⊤ L x x ⊤ x = ∑ ( i , j ) ∈ E ( x i − x j ) 2 ∑ i ∈ V x i 2 R(\mathrm{L}, \mathbf{x})=\frac{\mathbf{x}^{\top} \mathbf{L} \mathbf{x}}{\mathbf{x}^{\top} \mathbf{x}}=\frac{\sum_{(i, j) \in \mathcal{E}}\left(x_{i}-x_{j}\right)^{2}}{\sum_{i \in \mathcal{V}} x_{i}^{2}} R(L,x)=x⊤xx⊤Lx=∑i∈Vxi2∑(i,j)∈E(xi−xj)2
- 该商实际上是 x x x的标准化方差得分。 如上所述,平滑信号应在相邻节点上分配相似的值。 因此,具有较低瑞利商的信号被假定为更平滑。
考虑图的拉普拉斯特征分解: L = U Λ U − 1 \mathbf{L}=\mathbf{U} \mathbf{\Lambda} \mathbf{U}^{-1} L=UΛU−1, U ∈ R n × n \mathbf{U} \in \mathbb{R}^{n \times n} U∈Rn×n组成特征向量, Λ = diag ( λ 1 , λ 2 , ⋯ , λ n ) \Lambda=\operatorname{diag}\left(\lambda_{1}, \lambda_{2}, \cdots, \lambda_{n}\right) Λ=diag(λ1,λ2,⋯,λn)是特征值的对角矩阵。所以特征向量 u i u_i ui的平滑为:
R ( L , u i ) = u i ⊤ L u i u i ⊤ u i = λ i R\left(\mathbf{L}, \mathbf{u}_{i}\right)=\frac{\mathbf{u}_{i}^{\top} \mathbf{L} \mathbf{u}_{i}}{\mathbf{u}_{i}^{\top} \mathbf{u}_{i}}=\lambda_{i} R(L,ui)=ui⊤uiui⊤Lui=λi
- 该等式表示更平滑的特征向量与较小的特征值相关联,这意味着频率较低。
因此,作者基于上述两个等式创造出如下信号 x x x:
x = U p = ∑ i = 1 n p i u i \mathbf{x}=\mathbf{U p}=\sum_{i=1}^{n} p_{i} \mathbf{u}_{i} x=Up=i=1∑npiui
- p i p_i pi是特征向量 u i u_i ui的系数。
至此, x x x的平滑实际上是:
R ( L , x ) = x ⊤ L x x ⊤ x = ∑ i = 1 n p i 2 λ i ∑ i = 1 n p i 2 R(\mathbf{L}, \mathbf{x})=\frac{\mathbf{x}^{\top} \mathbf{L} \mathbf{x}}{\mathbf{x}^{\top} \mathbf{x}}=\frac{\sum_{i=1}^{n} p_{i}^{2} \lambda_{i}}{\sum_{i=1}^{n} p_{i}^{2}} R(L,x)=x⊤xx⊤Lx=∑i=1npi2∑i=1npi2λi
- 因此,为了获得更平滑的信号,我们的滤波器的目标是在滤除高频分量的同时保留低频分量。 由于其高计算效率和令人信服的性能,拉普拉斯平滑滤波器[28]通常用于此目的.
2.1.2 广义拉普拉斯平滑滤波器
广义拉普拉斯平滑滤波器被定义为:
H = I − k L \mathbf{H}=\mathbf{I}-k \mathbf{L} H=I−kL
- k k k是一个实值。
使用 H \mathbf{H} H作为滤波器矩阵,被过滤的信号 x ~ \tilde{\mathbf{x}} x~为:
x ~ = H x = U ( I − k Λ ) U − 1 U p = ∑ i = 1 n ( 1 − k λ i ) p i u i = ∑ i = 1 n p ′ i u i \tilde{\mathbf{x}}=\mathbf{H x}=\mathbf{U}(\mathbf{I}-k \mathbf{\Lambda}) \mathbf{U}^{-1} \mathbf{U} \mathbf{p}=\sum_{i=1}^{n}\left(1-k \lambda_{i}\right) p_{i} \mathbf{u}_{i}=\sum_{i=1}^{n} p^{\prime} i \mathbf{u}_{i} x~=Hx=U(I−kΛ)U−1Up=i=1∑n(1−kλi)piui=i=1∑np′iui
因此,为了实现低通滤波,频率响应函数1-应该是一个减量和非负函数。 堆叠Laplacian平滑滤波器,我们将滤波后的特征矩阵表示为:
X ~ = H t X \tilde{\mathbf{X}}=\mathbf{H}^{t} \mathbf{X} X~=HtX
- 注意到,滤波器中是没有参数的
2.1.3 k的选择
在实际中,使用重归一化技巧: A ~ = I + A \tilde{A}=I+A A~=I+A,作者设计一个对称归一化图拉普拉斯:
L ~ s y m = D ~ − 1 2 L ~ D ~ − 1 2 \tilde{\mathbf{L}}_{s y m}=\tilde{\mathbf{D}}^{-\frac{1}{2}} \tilde{\mathbf{L}} \tilde{\mathbf{D}}^{-\frac{1}{2}} L~sym=D~−21L~D~−21
- 其中 D ~ \tilde{\mathbf{D}} D~和 L ~ \tilde{\mathbf{L}} L~分别是与 A ~ \tilde{\mathbf{A}} A~相对应的度矩阵和拉普拉斯矩阵
然后滤波器变成:
H = I − k L ~ s y m \mathbf{H}=\mathbf{I}-k \tilde{\mathbf{L}}_{s y m} H=I−kL~sym
- 注意到,这里如果取 k = 1 k=1 k=1,则滤波器变成GCN滤波器。
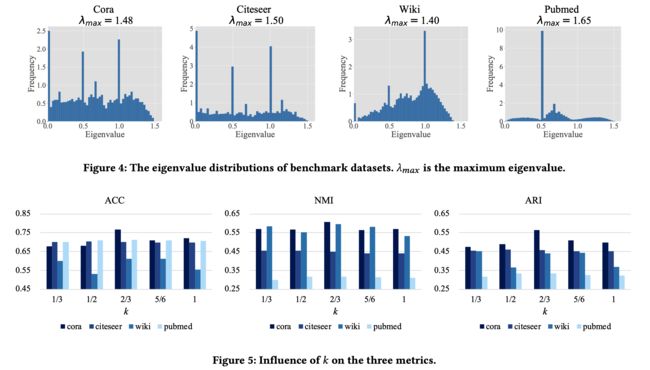
为了选择最佳 k k k,应该仔细地发现特征值 Λ ~ \tilde{\Lambda} Λ~的分布(从 L ~ s y m = U ~ Λ ~ U ~ − 1 \tilde{\mathbf{L}}_{s y m}=\tilde{\mathbf{U}} \tilde{\Lambda} \tilde{\mathbf{U}}^{-1} L~sym=U~Λ~U~−1的分解获得)。
x ~ \tilde{x} x~的平滑为:
R ( L , x ~ ) = x ~ ⊤ L x ~ x ~ ⊤ x ~ = ∑ i = 1 n p i 2 λ i ∑ i = 1 n p i 2 R(\mathrm{L}, \tilde{\mathrm{x}})=\frac{\tilde{\mathbf{x}}^{\top} \mathrm{L} \tilde{\mathbf{x}}}{\tilde{\mathbf{x}}^{\top} \tilde{\mathbf{x}}}=\frac{\sum_{i=1}^{n} p_{i}^{2} \lambda_{i}}{\sum_{i=1}^{n} p_{i}^{2}} R(L,x~)=x~⊤x~x~⊤Lx~=∑i=1npi2∑i=1npi2λi
- 因此, p ′ 2 p \prime^2 p′2随着 λ i \lambda_i λi增加应当减少。作者表示最大特征值为 λ m a x \lambda_{max} λmax。
- k < 1 / λ max k<1 / \lambda_{\max } k<1/λmax就不能滤除所有高频部分,
- k > 1 / λ max k>1 / \lambda_{\max } k>1/λmax,滤波器不是一个低通滤波器在 ( 1 / k , λ max ] \left(1 / k, \lambda_{\max }\right] (1/k,λmax]上,因为这段区间中, p ′ 2 p \prime^2 p′2随着 λ i \lambda_i λi增加而增加。
2.2 自适应编码
对于属性图嵌入任务,两个节点之间的关系至关重要,这要求训练目标是合适的相似性度量。作者认为GAE方法选用邻接矩阵作为节点对的真实标签仅仅记录了一跳的结构信息,这远远不够。同时,平滑特征或经过训练的嵌入的相似度更加准确,因为它们将结构和特征融合在一起。为此,作者自适应地选择相似度高的节点对作为正训练样本,而相似度低的节点对作为负训练样本。
节点嵌入通过被过滤的节点特征线性编码为:
Z = f ( X ~ ; W ) = X ~ W \mathbf{Z}=f(\tilde{\mathbf{X}} ; \mathbf{W})=\tilde{\mathbf{X}} \mathbf{W} Z=f(X~;W)=X~W
- W \mathbf{W} W是一个权重矩阵。
- 作者用了min-max scaler来讲嵌入缩减到[0,1]
作者使用余弦相似度来计算节点对的相似程度:
s = Z Z T ∥ Z ∥ 2 2 \mathrm{s}=\frac{\mathrm{ZZ}^{\mathrm{T}}}{\|\mathrm{Z}\|_{2}^{2}} s=∥Z∥22ZZT
2.2.1训练负样例选择:
r i j r_{ij} rij是节点对 ( v i , v j ) \left(v_{i}, v_{j}\right) (vi,vj)的相似度将排序rank。节点对 ( v i , v j ) \left(v_{i}, v_{j}\right) (vi,vj)的标签为:
l i j = { 1 r i j ≤ r p o s 0 r i j > r n e g None otherwise l_{i j}=\left\{\begin{array}{ll}1 & r_{i j} \leq r_{p o s} \\ 0 & r_{i j}>r_{n e g} \\ \text { None } & \text { otherwise }\end{array}\right. lij=⎩⎨⎧10 None rij≤rposrij>rneg otherwise
- 然后作者设置了正样例的最大rank值 r p o s r_{pos} rpos,和负样例的最小rank值 r n e g r_{neg} rneg。
用这种方法作者的训练集由 r p o s r_{pos} rpos个正样例和 n 2 − r n e g n^2-r_{neg} n2−rneg个负样例(因为负样例实际是远远多于正阳里的,所以这里作者生成的负样例比较多)
对于首次的训练集构建,由于encoder部分还未训练,直接应用平滑特征来计算初始的相似度矩阵:
S = X ~ X ~ ⊤ ∥ X ~ ∥ 2 2 \mathrm{S}=\frac{\tilde{\mathbf{X}} \tilde{\mathbf{X}}^{\top}}{\|\tilde{\mathbf{X}}\|_{2}^{2}} S=∥X~∥22X~X~⊤
在每个epoch中,作者随机采样 r p o s r_{pos} rpos个负样例来平和正负样例的数量。
作者采用交叉熵损失:
L = ∑ ( v i , v j ) ∈ O − l i j log ( s i j ) − ( 1 − l i j ) log ( 1 − s i j ) \mathcal{L}=\sum_{\left(v_{i}, v_{j}\right) \in O}-l_{i j} \log \left(s_{i j}\right)-\left(1-l_{i j}\right) \log \left(1-s_{i j}\right) L=(vi,vj)∈O∑−lijlog(sij)−(1−lij)log(1−sij)
2.2.2 阈值更新
受课程学习(curriculum learning)理念的启发,作者针对 r p o s r_{pos} rpos和 r n e g r_{neg} rneg设计了一种特定的更新策略,以控制训练集的大小。
在训练过程开始时,会为编码器选择更多样本以找到粗糙的聚类模式。 之后,将保留较高置信度的样本以进行训练,从而迫使编码器捕获精炼的模式。 实际上,随着训练过程的进行, r p o s r_{pos} rpos减小而 r n e g r_{neg} rneg线性增加。 所以作者设计了不同的开始和结束时的阈值,并随着更新的次数 T T T来不断变化,以达到动态调整。
r p o s ′ = r p o s + r p o s e d − r p o s s t T r n e g ′ = r n e g + r n e g e d − r n e g s t T \begin{array}{l}r_{p o s}^{\prime}=r_{p o s}+\frac{r_{p o s}^{e d}-r_{p o s}^{s t}}{T} \\ r_{n e g}^{\prime}=r_{n e g}+\frac{r_{n e g}^{e d}-r_{n e g}^{s t}}{T}\end{array} rpos′=rpos+Trposed−rposstrneg′=rneg+Trneged−rnegst
整个算法流程如下:
3 实验
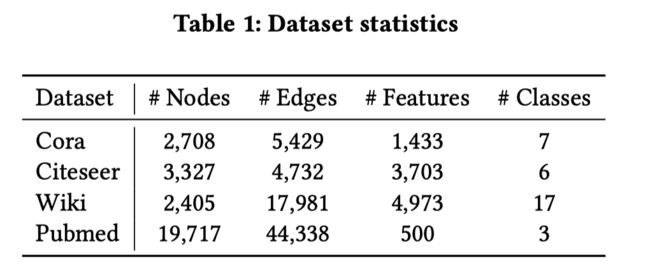
3.1 数据集
Features in Cora and Citeseer are binary word vectors, while in Wiki and Pubmed, nodes are associated with tf-idf weighted word vectors.
3.2 Baseline
- GAE and VGAE
- ARGA and ATVGA
- GALA
在节点聚类任务中可以分为以下三组:
- 只用特征模型:Kmeans 和 Spectral-Clustering
- 只用图结构模型:Spectral-G, DeepWalk
- 特征和图都用模型:TADW, MGAE, AGC, DAEGC
3.3 评价标准
节点聚类
- Accuracy (ACC), Normalized Mutual Information (NMI), and Adjusted Rand Index (ARI)
链接预测
- Area Under Curve (AUC) and Average Precision (AP) scores
3.4 实验结果
作者设计了辅助实验去回答以下三个假设:
- 滤波器和权重矩阵的纠缠对嵌入质量没有提升;
- 对比于重构损失,作者的自适应学习策略是有效的,并且每个机制有它自己的贡献;
- 对于拉普拉斯平滑滤波器 k = 1 / λ max k=1 / \lambda_{\max } k=1/λmax是最佳选择。
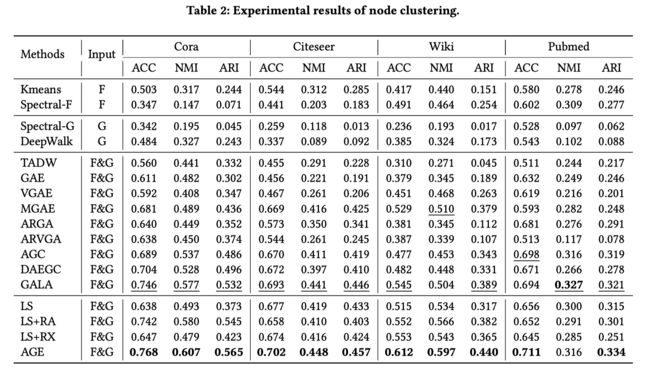
3.4.1 节点分类
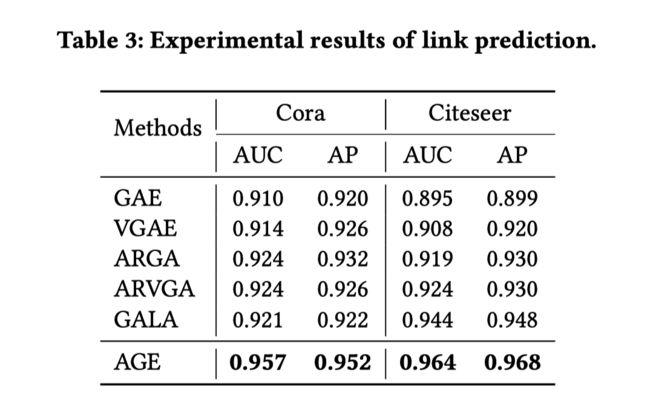
3.4.2 链接预测结果
作者使用简单的内积来得到预测的邻接矩阵:
A ^ = σ ( Z Z ⊤ ) \hat{\mathbf{A}}=\sigma\left(\mathbf{Z} \mathbf{Z}^{\top}\right) A^=σ(ZZ⊤)
- 其中 σ \sigma σ是sigmoid函数
GALA还为链接预测任务增加了重建损失,而AGE不使用显式链接进行监督。
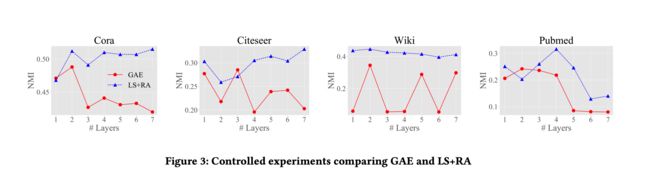
3.4.3 GAE v.s. LS+RA
回答假设1.滤波器和权重矩阵的纠缠对嵌入质量没有提升;
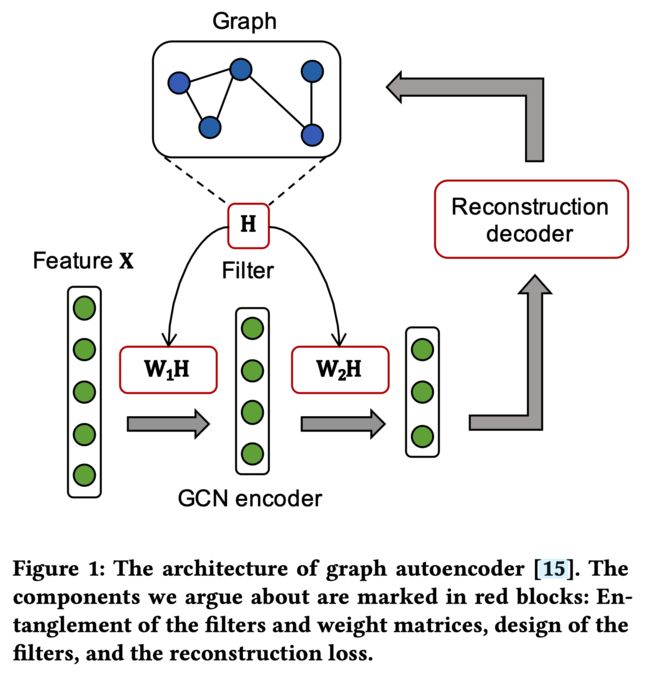
GAE在每一层中结合力权重矩阵和滤波器,如图一所示;
LS+RA把权重矩阵移动到滤波器之后。
3.4.4 消融实验
为了验证假设2:对比于重构损失,作者的自适应学习策略是有效的,并且每个机制有它自己的贡献;
LS+RA and LS+RX 展现出了可以和基线模型相比的表现,AGE模型要好于这两个模型说明自适应目标是更好的。
LS+RA 和 LS+RX分别在Cora, Wiki and Pubmed 和 Citeseer上表现效果更好。这说明了对于不同的数据集结构信息和特征信息的重要程度不同。此外,在Citeseer和Pubmed上,重建损失对平滑特征产生负面影响。
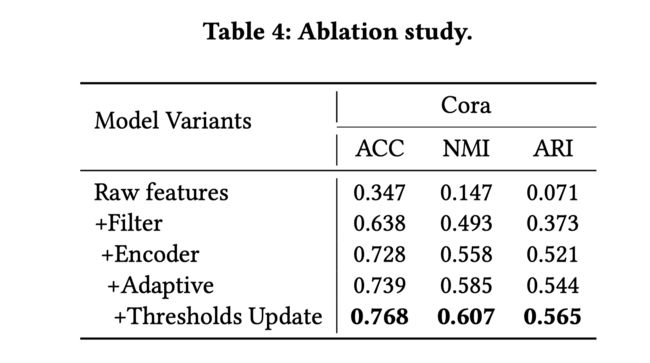
对Cora进行消融研究,以证明AGE中四种机制的功效。所有五个变体都通过对节点特征或嵌入的余弦相似度矩阵执行谱聚类来对节点进行聚类。
- “raw features”仅对原始节点特征执行频谱聚类;
- “ +Filter”使用平滑节点特征对节点进行聚类;
- “ +Encoder”从平滑节点特征的相似度矩阵初始化训练集,并通过固定的训练集学习节点嵌入;
- “ +Adaptive”以固定的阈值自适应地选择训练样本;
- “ +Thresholds Update”进一步添加了阈值更新策略,并且完全是完整模型。
3.4.5 k k k的选择
验证假设3:对于拉普拉斯平滑滤波器 k = 1 / λ max k=1 / \lambda_{\max } k=1/λmax是最佳选择。
3.4.6 可视化
参考链接
- 论文原文下载地址