神经网络中的BN操作（常见正则化处理）

1. BN简介

  BN的存在，主要起因于数据分布的问题。所谓数据分布，分为两种情况，一种在输入时数据分布不一样，称之为Covariate Shift，比如训练的数据和测试的数据本身分布就不一样，那么训练后的模型就很难泛化到测试集上。另一种分布不一样是指在输入数据经过网络内部计算后，分布发生了变化，使数据分布变得不稳定，从而导致网络寻找最优解的过程变得缓慢，训练速度会下降，这种称之为内部协方差偏移（Internal Covariate Shift）。

  内部协方差偏移为什么会影响网络训练：训练深度网络时，神经网络隐层参数更新会导致网络输出层输出数据的分布（相对于输入数据分布）发生变化，而且随着层数的增加，根据链式规则，这种偏移现象会逐渐被放大。这对于网络参数学习来说是个问题：因为神经网络本质学习的就是数据分布（representation learning），如果数据分布变化了，神经网络又需要学习新的分布。

  BN层的作用是对一个batch内的所有样本进行标准化，将不规范的样本分布变换为正态分布。处理后的样本数据分布于激活函数的敏感区域（梯度值较大的区域），因此在反向传播时能够加快误差的传播，加速网络训练。

1.1. 目前主流的归一化层介绍

  目前主要有这几个方法：

  Batch Normalization（2015年）：
Ioffe S, Szegedy C. Batch normalization: Accelerating deep network training by reducing internal covariate shift[C]//International conference on machine learning. PMLR, 2015: 448-456.

  Layer Normalization（2016年）：
Ba J L, Kiros J R, Hinton G E. Layer normalization[J]. arXiv preprint arXiv:1607.06450, 2016.

  Instance Normalization（2017年）：
Ulyanov D, Vedaldi A, Lempitsky V. Instance normalization: The missing ingredient for fast stylization[J]. arXiv preprint arXiv:1607.08022, 2016.

  Group Normalization（2018年）：
Wu Y, He K. Group normalization[C]//Proceedings of the European conference on computer vision (ECCV). 2018: 3-19.

  Switchable Normalization（2018年）：
Luo P, Ren J, Peng Z, et al. Differentiable learning-to-normalize via switchable normalization[J]. arXiv preprint arXiv:1806.10779, 2018.

  4种方法的示意图如下：

  假设输入图像大小为$[N,C,H,W]$简单来说，5种方法的主要区别在于：

  BN：将一个batch内的样本（$N$个样本），按照$N,H,W$三个维度进行标准化，也就是说，在每个通道上将所有的$N$个样本的$H,W$进行标准化操作。在batch较小时效果不好；

  LN：对特定的单个样本，按照$C,H,W$三个维度进行标准化，也就是说，对每个样本的所有通道上的$H,W$进行标准化操作。对RNN作用明显；

  IN：对特定的单个样本，按照$H,W$两个维度进行标准化，也就是说，对每个样本的每个通道上的$H,W$进行标准化操作。一般用于图像风格迁移任务中；

  GN：对特定的单个样本，将$C$分组，按照分组进行LN操作，也就是说，对每个样本特定通道上的$H,W$进行标准化操作；

  SN：将前面四种标准化方法结合，赋予权重，让网络自行学习归一化层如何选择。

1.2. Batch Normalization

  Batch Normalization的目标是将特征进行标准化，即使网络输入成为0均值标准差为1的正态分布。BN可以看成是对一个Batch（比如$N$）内的样本，按特征通道进行归一化（对每个通道上的样本进行归一化）。

  网络在训练中，样本数据通常是以batch的方式传入网络，因此每个batch的样本分布可能出现差异，通过BN操作使每个batch中的样本分布均变为标准正态分布，可以加速网络的训练；

  internal covarivate shift问题

  BN的操作流程：（假设这里的样本$x_i$均为单通道）

算法过程：

• 在当前通道上，计算每个batch内样本的均值${\mu }_{\mathcal{B}}$;
• 在当前通道上，计算每个batch内样本的方差${\sigma }_{\mathcal{B}}^2$;
• 对当前通道上的样本进行归一化操作；
• 引入缩放和平移操作。

import numpy as np

def Batchnorm(x, gamma, beta, bn_param):

    # x_shape:[B, C, H, W]
    running_mean = bn_param['running_mean']
    running_var = bn_param['running_var']
    results = 0.
    eps = 1e-5

    x_mean = np.mean(x, axis=(0, 2, 3), keepdims=True)
    x_var = np.var(x, axis=(0, 2, 3), keepdims=True0)
    x_normalized = (x - x_mean) / np.sqrt(x_var + eps)
    results = gamma * x_normalized + beta

    # 因为在测试时是单个图片测试，这里保留训练时的均值和方差，用在后面测试时用
    # 指数加权移动平均法(exponenentially weighted average)计算训练阶段中的均值和方差
    running_mean = momentum * running_mean + (1 - momentum) * x_mean
    running_var = momentum * running_var + (1 - momentum) * x_var

    bn_param['running_mean'] = running_mean
    bn_param['running_var'] = running_var

    return results, bn_param

  与Dropout类似，要保证训练阶段的输出和预测阶段的输出分布一致，那么就要进行一下处理（简单来说就是使用训练阶段的均值和方差的期望来对测试样本进行归一化）。

  因为训练数据时一般会用batch对样本进行划分，但是在验证或测试时，一次只会输入一条数据，没有均值和方差，如何对单条数据进行批标准化呢？针对这种情况，可以利用训练集中的均值和方差，下图是BN论文中的原图，1-6步是训练过程，7-12步是推断过程：

  在上述过程中，每个样本$x$的通道数为$K$，第$k$个通道上的样本为$x^{(k)}$。

  训练阶段对在每个通道上对样本进行归一化操作，并加入偏移和缩放操作得到$y$，通过损失函数优化原始的网络函数$\Theta$和BN层的参数$\{{\gamma }^{(k)},{\beta }^{(k)}{\}}_{k=1}^K$。

  冻结BN层的参数，即$N_{\text{BN}}^{\text{inf}}\leftarrow N_{\text{BN}}^{\text{tr}}$，完成样本的预测任务。

  求训练阶段每个batch的均值和方差的无偏估计，作为预测阶段的均值和方差，进行归一化操作，如：

$$y\leftarrow \gamma \left(\frac{x-E[x]}{\sqrt{Var[x]+ϵ}}\right)+\beta =\frac{\gamma }{\sqrt{Var[x]+ϵ}}x+\left[\beta -\frac{\gamma E[x]}{\sqrt{Var[x]+ϵ}}\right]$$

无偏估计：无偏估计是用样本统计量来估计总体参数时的一种无偏推断。

• 样本均值$\bar{X}$是样本总体期望$E[X]$的无偏估计；
• 样本二阶原点矩$A_2=\frac{1}{n}{\sum }_{i=1}^n{X}_i^2$是总体二阶原点矩${\mu }_2=E[X^2]的无偏估计$

1.3. 为什么BN层要加上scale和shift？

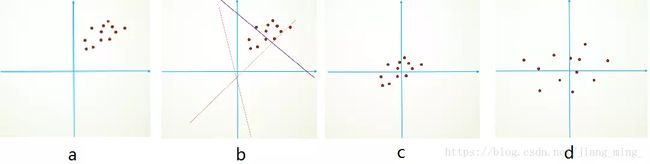
  首先解释下scale和shift的作用，以下图进行解释：

  假设原始输入数据如图a所示，完成二分类任务时划分超平面如图b所示。对原始数据进行平移操作，处理后数据如图c所示。可以看出相对于原始数据，平移后的数据更容易确定最优超平面的参数b；对平移后的数据进行缩放操作，如图d所示，可以看出处理后的数据差异性更大，更容易确定最优划分超平面。

  总得来说，平移和缩放操作是为了降低网络训练的难度，加速网络训练。

  BN进行缩放和平移操作的另一个原因是：假设强制对网络的每一层输入作归一化操作得到标准正态分布，当输入数据原始分布不符合标准正态分布时，很容易导致后层的网络学习不到输入数据的分布。因此，暴力归一化显然是不合理的。而BN中引入可学习的缩放和平移参数$\gamma ,\beta$目的就是，不会强制使分布变为正态分布，保留网络学习到输入分布的部分特性。甚至预测阶段的两个参数是通过训练集学习得到，因此能够通过两个参数使预测阶段的样本向训练集的整体分布靠近。所以，当训练样本和预测样本分布一致时，效果提升明显。

  另外一点，网络训练过程中，梯度受到输入的影响，假如输入$x$的分布不稳定（例如方差较大），会导致梯度值太大或太小，导致参数更新过程的不稳定。BN可以缓解这种不稳定的情况。

1.4 为什么BN可以是网络参数梯度变化较为稳定？

  上面提到BN可以使网络输出值变得较为稳定，从而使梯度变化较为稳定。也就是说，假设当输入缩放$\alpha$倍后，通过BN层的输出分布大致相同。因为，$x,W$相对于$\text{BN}\left(Wx\right)$和缩放$\alpha$倍后的权重输出$\text{BN}\left(\alpha Wx\right)$相等，即$\text{BN}\left(\alpha Wx\right)=\text{BN}\left(Wx\right)$，由此可以得出：
$$\frac{\partial \text{BN}\left((\alpha W)x\right)}{\partial x}=\frac{\partial \left(Wx\right)}{\partial x},\frac{\partial \text{BN}\left((\alpha W)x\right)}{\partial \alpha W}=\frac{1}{\alpha }\frac{\partial \left(Wx\right)}{\partial W}$$
可以看出，BN层可以减缓网络参数的梯度变化，因此可以使用更大的学习率加速训练。此外，BN的好处还有：

• Batch Normalization也可以帮助我们避免输入值经过饱和激活函数后陷入饱和区的现象。它可以确保不出现激活值太高或太低的情况，即梯度不会接近零。不使用BN时，权重很可能永远无法学习（梯度无限接近于零），BN也有助于减少对于参数初始值的依赖。
• BN能够减少训练时每层梯度的变化幅度，使梯度稳定在比较适合的变化范围内，减少了梯度对于参数尺度和初始值的依赖，降低了调参难度。且因为梯度变化更为稳定，因此可以使用更大尺度的学习率，加快网络收敛速度。
• BN作为一种正则化的形式，有助于减小过拟合问题。使用BN后，不需要太多的dropout，这是很有意义的。因为我们不需要再担心drop神经元时丢失太多的信息。当然两种技术也是能够结合使用的。

1.5 BN层在误差反向传播过程中如何工作？

  BN层的反向传播相比于普通层要略微复杂一些，首先给出论文中的公式，对其中省略的步骤在下面会给出推导过程。

  由于网络正向传播是根据$\gamma ,\beta$和均值、方差将$x_i$变换为$y_i$，那么反向传播则是根据$\frac{\partial \ell }{\partial y_i}$，计算出损失函数对于$\gamma ,\beta$以及$x_i$的偏导，其中对$x_i$求偏导则是为了将误差继续传播。BN层的输出为：$y_i={\text{BN}}_{\gamma ,\beta }\left(x_i\right)=\gamma {\hat{x}}_i+\beta$ 。

  通过分析，我们需要得到的$\frac{\partial \ell }{\partial x_i},\frac{\partial \ell }{\partial \gamma },\frac{\partial \ell }{\partial \beta }$，而${\hat{x}}_i,{\mu }_{\mathcal{B}},{\sigma }_{\mathcal{B}}^2$与$x_i$都有关系，即求解$\frac{\partial \ell }{\partial x_i}$可以分为：

$$\frac{\partial \ell }{\partial x_i}=\frac{\partial \ell }{\partial {\hat{x}}_i}\frac{\partial {\hat{x}}_i}{\partial x_i}+\frac{\partial \ell }{\partial {\mu }_{\mathcal{B}}}\frac{\partial {\mu }_{\mathcal{B}}}{\partial x_i}+\frac{\partial \ell }{\partial {\sigma }_{\mathcal{B}}^2}\frac{\partial {\sigma }_{\mathcal{B}}^2}{\partial x_i}$$

  第一项中：
$$\frac{\partial \ell }{\partial {\hat{x}}_i}=\frac{\partial \ell }{\partial y_i}\frac{\partial y_i}{\partial {\hat{x}}_i}=\frac{\partial \ell }{\partial y_i}\gamma$$

  先求损失$\ell$相对于参数${\mu }_{\mathcal{B}},{\sigma }_{\mathcal{B}}^2$的梯度：
$$\frac{\partial \ell }{\partial {\sigma }_{\mathcal{B}}^2}=\sum _{i=1}^m\frac{\partial \ell }{\partial {\hat{x}}_i}\frac{\partial {\hat{x}}_i}{\partial {\sigma }_{\mathcal{B}}^2}=\sum _{i=1}^m\frac{\partial \ell }{\partial {\hat{x}}_i}\cdot \left(x_i-{\mu }_{\mathcal{B}}\right)\cdot \frac{-1}{2}{\left({\sigma }_{\mathcal{B}}^2+ϵ\right)}^{-\frac{3}{2}}$$

参数${\sigma }_{\mathcal{B}}^2$与参数${\mu }_{\mathcal{B}}$相关，因此其梯度需要分为两部分：
$$\begin{array}{rl}\frac{\partial \ell }{\partial {\mu }_{\mathcal{B}}}& =\sum _{i=1}^m\frac{\partial \ell }{\partial {\hat{x}}_i}\frac{\partial {\hat{x}}_i}{\partial {\mu }_{\mathcal{B}}}+\frac{\partial \ell }{\partial {\sigma }_{\mathcal{B}}^2}\frac{\partial {\sigma }_{\mathcal{B}}^2}{\partial {\mu }_{\mathcal{B}}}\\ & =\sum _{i=1}^m\frac{\partial \ell }{\partial {\hat{x}}_i}\cdot \frac{-1}{\sqrt{{\sigma }_{\mathcal{B}}^2+ϵ}}+\frac{\partial \ell }{\partial {\sigma }_{\mathcal{B}}^2}\cdot \frac{{\sum }_{i=1}^m-2\left(x_i-{\mu }_{\mathcal{B}}\right)}{m}\end{array}$$

  下面求解$\frac{\partial \ell }{\partial x_i}$：
$$\begin{array}{rl}\frac{\partial \ell }{\partial x_i}& =\frac{\partial \ell }{\partial {\hat{x}}_i}\frac{\partial {\hat{x}}_i}{\partial x_i}+\frac{\partial \ell }{\partial {\hat{x}}_i}\frac{\partial {\hat{x}}_i}{\partial {\mu }_{\mathcal{B}}}\frac{\partial {\mu }_{\mathcal{B}}}{\partial x_i}+\frac{\partial \ell }{\partial {\hat{x}}_i}\frac{\partial {\hat{x}}_i}{\partial {\sigma }_{\mathcal{B}}^2}\frac{\partial {\sigma }_{\mathcal{B}}^2}{\partial x_i}\\ & =\frac{\partial \ell }{\partial {\hat{x}}_i}\frac{\partial {\hat{x}}_i}{\partial x_i}+\frac{\partial \ell }{\partial {\mu }_{\mathcal{B}}}\frac{\partial {\mu }_{\mathcal{B}}}{\partial x_i}+\frac{\partial \ell }{\partial {\sigma }_{\mathcal{B}}^2}\frac{\partial {\sigma }_{\mathcal{B}}^2}{\partial x_i}\\ & =\frac{\partial \ell }{\partial {\hat{x}}_i}\frac{1}{\sqrt{{\sigma }_{\mathcal{B}}^2+ϵ}}+\frac{\partial \ell }{\partial {\mu }_{\mathcal{B}}}\frac{1}{m}+\frac{\partial \ell }{\partial {\sigma }_{\mathcal{B}}^2}\frac{\partial {\sigma }_{\mathcal{B}}^2}{\partial x_i}\end{array}$$

注意：
$$\begin{array}{rl}\frac{\partial {\sigma }_{\mathcal{B}}^2}{\partial x_i}& =\frac{2}{m}\left(x_i-{\mu }_{\mathcal{B}}\right)\left(1-\frac{1}{m}\right)+\frac{2}{m}\sum _{k=1,k\ne i}^m\left(x_k-{\mu }_{\mathcal{B}}\right)\left(-\frac{1}{m}\right)\\ & =\frac{2}{m}\left(x_i-{\mu }_{\mathcal{B}}\right)+\frac{2}{m}\left(-\frac{1}{m}\right)\sum _{k=1}^m\left(x_k-{\mu }_{\mathcal{B}}\right)\\ & =\frac{2}{m}\left(x_i-{\mu }_{\mathcal{B}}\right)+\frac{2}{m}\left(-\frac{1}{m}\right)\left(\sum _{k=1}^m{x}_k-m{\mu }_{\mathcal{B}}\right)\\ & =\frac{2}{m}\left(x_i-{\mu }_{\mathcal{B}}\right)\end{array}$$

所以：
$$\frac{\partial \ell }{\partial x_i}=\frac{\partial \ell }{\partial {\hat{x}}_i}\frac{1}{\sqrt{{\sigma }_{\mathcal{B}}^2+ϵ}}+\frac{\partial \ell }{\partial {\mu }_{\mathcal{B}}}\frac{1}{m}+\frac{\partial \ell }{\partial {\sigma }_{\mathcal{B}}^2}\frac{2}{m}\left(x_i-{\mu }_{\mathcal{B}}\right)$$

再加上对$\gamma ,\beta$的偏导：
$$\begin{array}{rl}\frac{\partial \ell }{\partial \gamma }& =\sum _{i=1}^m\frac{\partial \ell }{\partial y_i}\frac{\partial y_i}{\partial \gamma }=\sum _{i=1}^m\frac{\partial \ell }{\partial y_i}{\hat{x}}_i\\ \frac{\partial \ell }{\partial \beta }& =\sum _{i=1}^m\frac{\partial \ell }{\partial y_i}\frac{\partial y_i}{\partial \beta }=\sum _{i=1}^m\frac{\partial \ell }{\partial y_i}\end{array}$$

1.6 为什么要保证训练和测试阶段的输出分布一致

  在Batch Normalization的论文中，作者将内部协方差偏移(Internal Covariate Shift)问题定义为由于训练期间网络参数的变化而导致网络激活值分布发生变化的现象。在 LeCun，Wiesler & Ney 等人的论文中可以知道，如果对神经网络的输入进行白化(whitened，zero means and unit variances)及去相关操作，那么可以消除Internal Covariate Shift的不良影响，从而加快神经网络的训练。而Batch Normalization的操作（还有之前Dropout中对参数或输出进行缩放scale等操作）和上述类似，也能起到消除Internal Covariate Shift的作用。

1.7 内部协方差偏移(Internal Covariate Shift)问题

1.7.1 深度网络难于训练的原因？

  训练深度网络时，神经网络隐层参数更新会导致网络输出数据的分布发生变化，而且随着层数增加，根据链式求导规则，这种偏移现象会被逐渐放大。这使得网络学习成为问题：因为网络的本质就是学习数据的分布，如果输出分布发生变化，网络不得不学习新的分布。为了保证网络参数训练的稳定性和收敛性，往往需要选择较小的学习速率，同时参数初始化的好坏也明显影响最终模型的精度。为了对模型进行训练，我们需要非常谨慎地去设定学习率、初始化权重、以及尽可能细致的参数更新策略。

  联系：输出分布发生变化，网络通过参数更新对分布进行拟合，若学习率选择不恰当，会使得网络始终无法拟合出新的分布，或者过程较慢，这就是训练中学习率不合适使得损失曲线发生抖动的原因吧。

  Google 将这一现象总结为 Internal Covariate Shift，简称 ICS。

  简单来说，将每一层的输入作为一个分布看待，由于深层的参数随着训练更新，导致相同输入分布得到的输出分布发生变化。

  而机器学习中有个很重要的假设：IID独立同分布假设，就是假设训练数据和测试数据是满足相同分布且相互独立，这是通过训练数据获得的模型能够在测试集获得好的效果的一个基本保障。

  那么，细化到神经网络的每一层间，每轮训练时分布都是不一致，那么相对的训练效果就得不到保障，所以称为层间的协方差偏移(covariate shift)。

  源空间：这里指的是已知的训练样本空间，即包括训练样本及其样本标记；

  目标空间：指未知的测试样本空间，我们要预测的是其样本标记。

   即当源域数据和目标域数据分布一致时，满足源域和目标域的特征空间和标记空间相同。

  在统计机器学习中的一个经典假设是“源空间(source domain)和目标空间(target domain)的数据分布(distribution)是一致的”。如果不一致，那么就出现了新的机器学习问题，如迁移学习和域自适应(transfer learning, domain adaptation)等。而covariate shift就是分布不一致假设之下的一个分支问题，它是指源空间和目标空间的条件概率是一致的，但是其边缘概率不同，即：

对所有$x\in \mathcal{X}$ ，有：$P_s\left(Y|X=x\right)=P_t\left(Y|X=x\right)$ 。
但是，$P_s\left(X\right)\ne P_t\left(X\right)$ 。

  对于神经网络的各层输出，由于相同分布的样本经过了层内操作作用（输入分布经过多次线性、非线性变换），原本的样本分布显然与各层对应的输入信号分布不同，而且差异会随着网络深度增大而增大，可是样本对应的样本标签(label)仍然是不变的，这便符合了covariate shift的定义，即条件概率$P\left(Y|X\right)$一致，边缘概率$P\left(X\right)$不同。由于是对层间信号的分析，也即是“internal”的来由。

  因此，每个神经元的输入数据不再是“独立同分布”，导致了以下问题：

• 深层网络需要不断适应新的输入数据分布，学习速度降低。
• 浅层输入的变化可能趋向于变大或者变小，导致深层落入饱和区，使得学习过早停止。
• 每层参数的更新都会影响到其它层，因此参数更新策略需要尽可能的谨慎。

1.7.2 解决ICS内部协方差偏移的方法：

  前面说到，出现上述问题的根本原因是神经网络每层之间，无法满足基本假设“独立同分布”，那么思路应该是怎么使得相同输入对应的输出分布满足独立同分布。

白化(Whitening)

  白化，是机器学习里面常用的一种规范化数据分布的方法，主要是PCA白化与ZCA白化。在PCA中介绍过。

  PCA白化大致过程为：第一步操作是PCA操作，求出新特征空间中的新坐标，第二步是对新的坐标进行方差归一化操作。

  ZCA白化即通过投影矩阵将PCA白化操作后的归一化坐标重新投影至原特征空间中。

  白化是对输入数据分布进行变换，进而达到以下两个目的：

  1、使得输入特征分布具有相同的均值与方差，其中PCA白化保证了所有特征分布均值为0，方差为1；而ZCA白化则保证了所有特征分布均值为0，方差相同；

  2、去除特征之间的相关性。协方差矩阵中非对角元素为零。
通过白化操作，我们可以减缓ICS的问题，进而固定了每一层网络输入分布，加速网络训练过程的收敛。

  因为白化操作比较复杂，而BN论文作者认为BN操作可以缓解内部协方差偏移ICS问题。我们知道BN得到的是均值和方差相同的分布，但是保值均值和方差一致的分布也不一定是同分布。所以ICS问题是BN论文的一种升华方式。BN操作实际上并不是直接去解决ICS问题，更多的是解决了梯度消失等问题，以此来加速网络收敛的。

参考：https://www.zhihu.com/question/38102762/answer/85238569

BN代码实现：

  下面给出BN层的前向算法和反向传播的Python实现。
前面说过，论文中采用的是指数加权移动平均法(exponenentially weighted average)，也叫滑动平均(Moving Average)模型，最后利用无偏估计量进行预测。在这里介绍另一种方案（相当于累计更新），利用一个动量参数$\theta$得到一个动态均值 $r{\mu }_{\mathcal{B}}$ 与动态方差$r{\sigma }_{\mathcal{B}}^2$，这样更方便简洁，torch7采用的也是这种方法，具体公式如下（其中${\mathcal{B}}_i$表示的是第$i$个mini-batch）：

$$r{\mu }_{{\mathcal{B}}_i}=\theta r{\mu }_{{\mathcal{B}}_{i-1}}+\left(1-\theta \right){\mu }_{\mathcal{B}}$$
$$rr{\sigma }_{{\mathcal{B}}_i}^2=\theta r{\sigma }_{{\mathcal{B}}_{i-1}}^2+\left(1-\theta \right){\sigma }_{\mathcal{B}}^2$$

BN层前向传播：

def batchnorm_forward(x, gamma, beta, bn_param):
    """
    Forward pass for batch normalization.

    Input:
    - x: Data of shape (N, D)
    - gamma: Scale parameter of shape (D,)
    - beta: Shift paremeter of shape (D,)
    - bn_param: Dictionary with the following keys:
    - mode: 'train' or 'test'; required
    - eps: Constant for numeric stability
    - momentum: Constant for running mean / variance.   ## 计算均值、方差时用到的常数
    - running_mean: Array of shape (D,) giving running mean of features
    - running_var Array of shape (D,) giving running variance of features

    Returns a tuple of:
    - out: of shape (N, D)
    - cache: A tuple of values needed in the backward pass
    """

    mode = bn_param['mode']
    eps = bn_param.get('eps', 1e-5)
    momentum = bn_param.get('momentum', 0.9)

    N, D = x.shape
    running_mean = bn_param.get('running_mean', np.zeros(D, dtype=x.dtype))
    running_var = bn_param.get('running_var', np.zeros(D, dtype=x.dtype))

    out, cache = None, None
    
    if mode == 'train':

        sample_mean = np.mean(x, axis=0)
        sample_var = np.var(x, axis=0)
        out_ = (x - sample_mean) / np.sqrt(sample_var + eps)
        # 更新均值和方差
        running_mean = momentum * running_mean + (1 - momentum) * sample_mean
        running_var = momentum * running_var + (1 - momentum) * sample_var
        # BN层的输出
        out = gamma * out_ + beta
        cache = (out_, x, sample_var, sample_mean, eps, gamma, beta)

    elif mode == 'test':
        # 可以看出测试阶段，使用的是running_mean参数提供的均值
        scale = gamma / np.sqrt(running_var + eps)
        out = x * scale + (beta - running_mean * scale)    

    else:
        raise ValueError('Invalid forward batchnorm mode "%s"' % mode)

    # Store the updated running means back into bn_param
    bn_param['running_mean'] = running_mean
    bn_param['running_var'] = running_var

    return out, cache

BN层的反向传播：

def batchnorm_backward(dout, cache):
    """
    Backward pass for batch normalization.

    Inputs:
    - dout: Upstream derivatives, of shape (N, D)
    - cache: Variable of intermediates from batchnorm_forward.

    Returns a tuple of:
    - dx: Gradient with respect to inputs x, of shape (N, D)
    - dgamma: Gradient with respect to scale parameter gamma, of shape (D,)
    - dbeta: Gradient with respect to shift parameter beta, of shape (D,)
    """
    # 初始化偏导
    dx, dgamma, dbeta = None, None, None
    # 获得所需参数
    out_, x, sample_var, sample_mean, eps, gamma, beta = cache

    N = x.shape[0]
    dout_ = gamma * dout   # dl/d(hat(x))=dl/dy*gamma
    dvar = np.sum(dout_ * (x - sample_mean) * -0.5 * (sample_var + eps) ** -1.5, axis=0)
    dx_ = 1 / np.sqrt(sample_var + eps)  # d(hat(x))/dx
    dvar_ = 2 * (x - sample_mean) / N   # dvar/dx

    # intermediate for convenient calculation
    di = dout_ * dx_ + dvar * dvar_     # dl/dx的前两项：dl/d(hat(x))* d(hat(x))/dx + dl/dvar* dvar/dx
    dmean = -1 * np.sum(di, axis=0)    # dl/dmean
    dmean_ = np.ones_like(x) / N      # dmean/dx

    dx = di + dmean * dmean_         # dl/dx
    dgamma = np.sum(dout * out_, axis=0)   # dl/dgamma
    dbeta = np.sum(dout, axis=0)           # dl/dbeta

    return dx, dgamma, dbeta

参考：https://zhuanlan.zhihu.com/p/26138673

2 Layer Normalization

  Batch Normalizaiton存在以下缺点：

• 对batch size的大小比较敏感，由于每次在一个batch上计算均值和方差，所以batch size太小，则计算的均值和方差不足以代表整个数据分布；
• BN实际使用时，需要计算并且保存某一层神经网络batch的均值和方差等统计信息，对于固定深度的神经网络使用BN很方便；但对于RNN来说，sequence的长度不一致，也就是说RNN的深度不是固定的，不同的time-step需要保存不同的状态特征，可能存在一个临时的sequence更长。在训练时，计算就很麻烦。

• 与BN不同，Layer Normalization是针对深度网络的某一层的所有神经元的输入进行正则化操作。LN可以看成是按同一个样本的所有特征通道进行归一化。

  假设第$i$个数据为$a^i$其通道数为$L$，对该数据进行层归一化时均值和标准差为：
$${\mu }_i=\frac{1}{L}\sum _{l=1}^L{a}_i^l,{\sigma }_i=\sqrt{\frac{1}{L}\sum _{l=1}^L{\left(a_i^l-{\mu }^l\right)}^2}$$

  BN与Layer Normalization的区别在于：

• LN中同一样本的不同通道具有相同的均值的方差，不同的输入样本有不同的均值和方差；
• BN中则针对不同输入样本计算均值和方差，同一个batch中的输入具有相同的均值和方差。

  所以，LN不依赖于Batch的大小和输入Sequence的深度（也就是通道数），因此可以用于batch size为1和输入长度变化sequence的正则化操作。LN用在RNN上效果比较明显。

3 Instance Normalization

  BN注重对每个batch进行归一化，保证每个Batch内数据分布一致（均值和方差相同），因此模型的训练结果取决于每个Batch内数据的整体分布。

  但是在图像风格化迁移问题中，生成结果主要依赖于某个图像实例，所以对整个batch进行归一化，不适合该问题，因而对单个实例进行归一化。可以加速模型收敛，并且保持每个图像实例之间的独立性。（以图像为例，便是对每个图像的像素进行归一化）

  对当前batch内的第$t$个样本的第$i$个通道上的图像进行归一化，如下：

$$\begin{gathered} {\mu }_{ti}=\frac{1}{HW}\sum _{l=1}^W\sum _{m=1}^H{x}_{tilm},{\sigma }_{ti}^2=\frac{1}{HW}\sum _{l=1}^W\sum _{m=1}^H{\left(x_{tilm}-{\mu }_{ti}\right)}^2, \\ {y}_{tijk}=\frac{x_{tijk}-{\mu }_{ti}}{\sqrt{{\sigma }_{ti}^2+ϵ}} \end{gathered}$$

  Instance Normalization对于一些图片生成类的任务比如图片风格转换来说效果是明显优于BN的，但在很多其它图像类任务比如分类等场景效果不如BN。

  BN的计算受其他样本影响的，由于每个batch的均值和标准差不稳定，对于单个数据而言，相对于是引入了噪声，但在分类这种问题上，结果和数据的整体分布有关系，因此需要通过BN获得数据的整体分布。而instance normalization的信息都是来自于自身的图片，相当于对全局信息做了一次整合和调整，在图像转换这种问题上，BN获得的整体信息不会带来任何收益，带来的噪声反而会弱化实例之间的独立性：这类生成式方法，每张图片自己的风格比较独立不应该与batch中其他的样本产生太大联系。

4 Group Normalization

  同样是解决BN对小batch效果较差的问题，Group Normalization将通道分组，然后对每个组内进行归一化，因此也与Batch大小无关。GN与Layer Norm类似，不过Group Norm将图像的特征通道分组，对每一组进行LN（即对单个样本的部分通道上的特征进行归一化。）

  将样本的通道数进行分组，具体为：$S_i=\left\{k|k_N=iN,\lfloor \frac{k_C}{\frac{C}{G}}\rfloor =\lfloor \frac{i_C}{\frac{C}{G}}\rfloor \right\}$，其中$\lfloor \frac{k_C}{\frac{C}{G}}\rfloor =\lfloor \frac{i_C}{\frac{C}{G}}\rfloor$是指：通道$k_C,i_C$被分为同一组中；$\{k|k_N=i_N\}$是指按照Batch的单个样本进行组归一化操作。

  tf.nn.moments(x,[2, 3, 4], keep_dims=True)：按维度[2,3,4]求解均值和方差，并保持维度不变。这里的输入样本矩阵为$\left[\text{N,C,H,W}\right]$，首先进行变形$\left[N,C,\text{C//}G,\text{H,W}\right]$，然后按照维度$\left[:,\text{C//}G,\text{H,W}\right]$求均值和方差。当Batch size不为0时，需要对batch内的每个样本按通道分组归一化。

5 Switchable Normalization

  论文作者认为：

• 归一化虽然提高模型的泛化能力，但是归一化操作是人工设计的。在实际应用中，解决不同的问题原则上需要设计不同的归一化操作，并没有通用的归一化方法；
• 一个深度网络往往包含几十个归一化层，通常这些归一化层都使用的是相同的归一化策略，因为，给每一个归一化层手工设计不同的策略需要进行大量的实验。

  因此作者提出自适应归一化方法——Switchable Normalization(SN)来解决上述问题。与强化学习不同，SN可以通过可微分学习，为深度网络中的每一个归一化层确定合适的归一化操作。

  SN有一个直观表达：
通过网络学习各类归一化方法的权重 ，来结合BN，Layer Norm，Instance Norm等归一化操作。

$$\begin{array}{rl}{\hat{h}}_{ncij}& =\gamma \frac{h_{ncij}-{\sum }_{k\in \Omega }{w}_k{\mu }_k}{\sqrt{{\sum }_{k\in \Omega }{w}_k^{{}^{\prime }}{\sigma }_k^2+ϵ}}+\beta \\ w_k& =\frac{e^{{\lambda }_k}}{{\sum }_{z\in \left\{\text{in,}\ln \text{,bn}\right\}}{e}^{{\lambda }_z}},k\in \left\{\text{in,}\ln \text{,bn}\right\}\end{array}$$

$$\begin{gathered} {\mu }_{\text{in}}=\frac{1}{HW}\sum _{i,j}^{H,W}{h}_{ncij},{\sigma }_{\text{in}}^2=\frac{1}{HW}\sum _{i,j}^{H,W}{\left(h_{ncij}-{\mu }_{\text{in}}\right)}^2 \\ {\mu }_{\ln }=\frac{1}{C}\sum _{c=1}^C{\mu }_{\text{in}},{\sigma }_{\ln }^2=\frac{1}{C}\sum _{c=1}^C\left({\sigma }_{\text{in}}^2+{\mu }_{\text{in}}^2\right)-{\mu }_{\ln }^2 \\ {\mu }_{\text{bn}}=\frac{1}{N}\sum _{n=1}^N{\mu }_{\text{in}},{\sigma }_{\text{bn}}^2=\frac{1}{N}\sum _{n=1}^N\left({\sigma }_{\text{in}}^2+{\mu }_{\text{in}}^2\right)-{\mu }_{\text{bn}}^2 \end{gathered}$$

其中，$h_{ncij}$表示当前样本（以图像为例）中，第$c$个通道上位置$(i,j)$处的像素值。因为归一化后的值${\hat{h}}_{ncij}$

  原文中作者进行的实验结果分析：

• 从图(a)可以看出，采用SN策略的不同任务，模型学习出的4种正则化策略的比重也不同。比如在图像风格迁移中由于单个样本实例影响较大，因此主要起作用的是IN；而LSTM中权重最大的则是LN。

• 从图(b)可以看出当batch size较小时（即图中所说每个GPU的样本数），当$N$减小到一定程度时准确度急剧下降，当$N$增大时准确度又能提升，而Instance Norm(Ideal BN)与$N$无关，GN与$N$也无关，这里结果出现波动可能是因为其他因素。而融合的SN也会受到batch size的影响。

优缺点： 简单总结下，SN方法通过训练得到针对于特定任务的归一化方法组合{BN, IN, LN}，使网络不会受到某个方法缺陷所制约（如Batch太小时，BN效果不好，但是SN训练得到的BN权重较小，减缓了该问题）。此外，无须针对网络的特定层数来设计归一化方法。但是，缺陷之处在于增加了网络训练的难度。

5.1 SN pytorch源码

来源：https://github.com/switchablenorms/Switchable-Normalization

class SwitchNorm2d(nn.Module):
    def __init__(self, num_features, eps=1e-5, momentum=0.9, using_moving_average=True, using_bn=True,
                 last_gamma=False):
        super(SwitchNorm2d, self).__init__()
        self.eps = eps
        self.momentum = momentum
        self.using_moving_average = using_moving_average
        self.using_bn = using_bn
        self.last_gamma = last_gamma
        self.weight = nn.Parameter(torch.ones(1, num_features, 1, 1))
        self.bias = nn.Parameter(torch.zeros(1, num_features, 1, 1))
        if self.using_bn:
            self.mean_weight = nn.Parameter(torch.ones(3))
            self.var_weight = nn.Parameter(torch.ones(3))
        else:
            self.mean_weight = nn.Parameter(torch.ones(2))
            self.var_weight = nn.Parameter(torch.ones(2))
        if self.using_bn:
            self.register_buffer('running_mean', torch.zeros(1, num_features, 1))
            self.register_buffer('running_var', torch.zeros(1, num_features, 1))

        self.reset_parameters()

    def reset_parameters(self):
        if self.using_bn:
            self.running_mean.zero_()
            self.running_var.zero_()
        if self.last_gamma:
            self.weight.data.fill_(0)
        else:
            self.weight.data.fill_(1)
        self.bias.data.zero_()

    def _check_input_dim(self, input):
        if input.dim() != 4:
            raise ValueError('expected 4D input (got {}D input)'
                             .format(input.dim()))

    def forward(self, x):
        self._check_input_dim(x)
        N, C, H, W = x.size()
        x = x.view(N, C, -1)    # [N, C, W*H]
        mean_in = x.mean(-1, keepdim=True)    # 根据W*H这一维度计算均值（IN）
        var_in = x.var(-1, keepdim=True)

        mean_ln = mean_in.mean(1, keepdim=True)    # LN相对于IN需要对求出所有通道上的均值
        temp = var_in + mean_in ** 2
        var_ln = temp.mean(1, keepdim=True) - mean_ln ** 2

        if self.using_bn:
            if self.training:
                mean_bn = mean_in.mean(0, keepdim=True)    # 按照N求均值
                var_bn = temp.mean(0, keepdim=True) - mean_bn ** 2
                if self.using_moving_average:
                    self.running_mean.mul_(self.momentum)
                    self.running_mean.add_((1 - self.momentum) * mean_bn.data)
                    self.running_var.mul_(self.momentum)
                    self.running_var.add_((1 - self.momentum) * var_bn.data)
                else:
                    self.running_mean.add_(mean_bn.data)
                    self.running_var.add_(mean_bn.data ** 2 + var_bn.data)
            else:
                mean_bn = torch.autograd.Variable(self.running_mean)
                var_bn = torch.autograd.Variable(self.running_var)

        softmax = nn.Softmax(dim=0)    # 按列进行归一化
        mean_weight = softmax(self.mean_weight)    # 权重归一化
        var_weight = softmax(self.var_weight)

        if self.using_bn:
            mean = mean_weight[0] * mean_in + mean_weight[1] * mean_ln + mean_weight[2] * mean_bn
            var = var_weight[0] * var_in + var_weight[1] * var_ln + var_weight[2] * var_bn
        else:
            mean = mean_weight[0] * mean_in + mean_weight[1] * mean_ln
            var = var_weight[0] * var_in + var_weight[1] * var_ln

        x = (x-mean) / (var+self.eps).sqrt()
        x = x.view(N, C, H, W)
        return x * self.weight + self.bias