NNDL 实验六 卷积神经网络(2)基础算子
目录
卷积神经网络的基础算子
卷积层算子
多通道卷积
多通道卷积层算子
卷积算子的参数量和计算量
汇聚层算子
选做题
使用pytorch实现Convolution Demo
总结
参考
卷积神经网络的基础算子
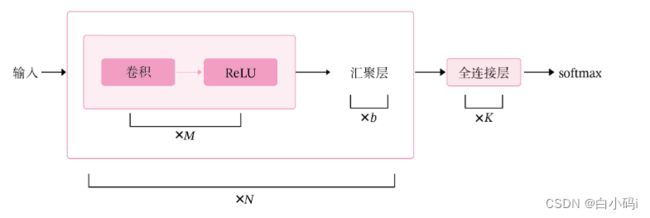
卷积神经网络是目前计算机视觉中使用最普遍的模型结构，如下图所示，由M个卷积层和b个汇聚层组合作用在输入图片上，在网络的最后通常会加入K个全连接层。
从上图可以看出，卷积网络是由多个基础的算子组合而成。下面我们先实现卷积网络的两个基础算子：卷积层算子和汇聚层算子。
首先我们实现卷积网络的两个基础算子：卷积层算子和汇聚层算子
卷积层算子
卷积层是指用卷积操作来实现神经网络中一层。
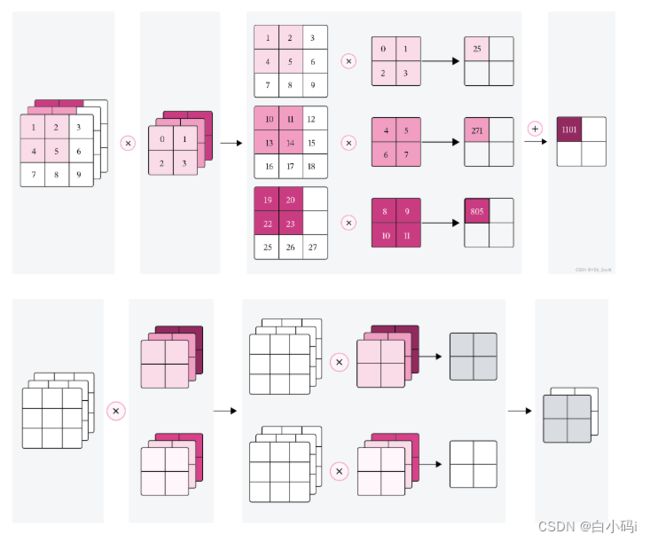
为了提取不同种类的特征，通常会使用多个卷积核一起进行特征提取。
多通道卷积
多通道卷积层算子
1. 多通道卷积卷积层的代码实现
2. Pytorch：torch.nn.Conv2d()代码实现
3. 比较自定义算子和框架中的算子
代码实现：
import torch
import torch.nn as nn
class Conv2D(nn.Module):
def __init__(self, in_channels, out_channels, kernel_size, stride=1, padding=0,weight_attr=[],bias_attr=[]):
super(Conv2D, self).__init__()
# 创建卷积核
weight_attr = torch.randn([out_channels, in_channels, kernel_size, kernel_size])
weight_attr = torch.nn.init.constant(torch.tensor(weight_attr, dtype=torch.float32), val=1.0)
self.weight = torch.nn.Parameter(weight_attr)
# 创建偏置
bias_attr = torch.zeros([out_channels, 1])
bias_attr = torch.tensor(bias_attr, dtype=torch.float32)
self.bias = torch.nn.Parameter(bias_attr)
self.stride = stride
self.padding = padding
# 输入通道数
self.in_channels = in_channels
# 输出通道数
self.out_channels = out_channels
# 基础卷积运算
def single_forward(self, X, weight):
# 零填充
new_X = torch.zeros([X.shape[0], X.shape[1]+2*self.padding, X.shape[2]+2*self.padding])
new_X[:, self.padding:X.shape[1]+self.padding, self.padding:X.shape[2]+self.padding] = X
u, v = weight.shape
output_w = (new_X.shape[1] - u) // self.stride + 1
output_h = (new_X.shape[2] - v) // self.stride + 1
output = torch.zeros([X.shape[0], output_w, output_h])
for i in range(0, output.shape[1]):
for j in range(0, output.shape[2]):
output[:, i, j] = torch.sum(new_X[:, self.stride*i:self.stride*i+u, self.stride*j:self.stride*j+v]*weight, [1, 2])
return output
def forward(self, inputs):
"""
输入：
- inputs：输入矩阵，shape=[B, D, M, N]
- weights：P组二维卷积核，shape=[P, D, U, V]
- bias：P个偏置，shape=[P, 1]
"""
feature_maps = []
# 进行多次多输入通道卷积运算
p=0
for w, b in zip(self.weight, self.bias): # P个(w,b),每次计算一个特征图Zp
multi_outs = []
# 循环计算每个输入特征图对应的卷积结果
for i in range(self.in_channels):
single = self.single_forward(inputs[:, i, :, :], w[i])
multi_outs.append(single)
# print("Conv2D in_channels:",self.in_channels,"i:",i,"single:",single.shape)
# 将所有卷积结果相加
feature_map = torch.sum(torch.stack(multi_outs), 0) + b # Zp
feature_maps.append(feature_map)
# print("Conv2D out_channels:",self.out_channels, "p:",p,"feature_map:",feature_map.shape)
p+=1
# 将所有Zp进行堆叠
out = torch.stack(feature_maps, 1)
return out
inputs = torch.tensor([[[[0.0, 1.0, 2.0], [3.0, 4.0, 5.0], [6.0, 7.0, 8.0]],
[[1.0, 2.0, 3.0], [4.0, 5.0, 6.0], [7.0, 8.0, 9.0]]]])
conv2d = Conv2D(in_channels=2, out_channels=3, kernel_size=2)
print("inputs shape:", inputs.shape)
outputs = conv2d(inputs)
print("Conv2D outputs shape:", outputs.shape)
# 比较与torch API运算结果
weight_attr = torch.ones([3, 2, 2, 2])
bias_attr = torch.zeros([3, 1])
bias_attr = torch.tensor(bias_attr,dtype=torch.float32)
conv2d_torch = nn.Conv2d(in_channels=2, out_channels=3, kernel_size=2, bias=True)
conv2d_torch.weight = torch.nn.Parameter(weight_attr)
outputs_torch = conv2d_torch(inputs)
# 自定义算子运算结果
print('Conv2D outputs:', outputs)
# torch API运算结果
print('nn.Conv2D outputs:', outputs_torch)实现效果：
inputs shape: torch.Size([1, 2, 3, 3])
Conv2D outputs shape: torch.Size([1, 3, 2, 2])
Conv2D outputs: tensor([[[[20., 28.],
[44., 52.]],[[20., 28.],
[44., 52.]],[[20., 28.],
[44., 52.]]]], grad_fn=)
nn.Conv2D outputs: tensor([[[[20.0537, 28.0537],
[44.0537, 52.0537]],[[20.1784, 28.1784],
[44.1784, 52.1784]],[[20.1576, 28.1576],
[44.1576, 52.1576]]]], grad_fn=)
卷积算子的参数量和计算量
卷积层的参数量计算
卷积核（kernel）的参数量：
滤波器（filter）的参数量：
bias参数量：
总的参数量：
卷积操作的计算量
乘法计算量：为了得到输出feature map的一个像素点，需要进行
次乘法操作。因此为了得到整个输出feature map，需要进行
加法计算量：为了得到输出feature map的一个像素点，需要进行
次加法操作。注意最后一个1是bias。因此为了得到整个输出feature map，需要进行次加法。
可以发现，加法与乘法计算量是一样的。
参考：卷积中参数量和计算量
汇聚层算子
汇聚层的作用是进行特征选择，降低特征数量，从而减少参数数量。由于汇聚之后特征图会变得更小，如果后面连接的是全连接层，可以有效地减小神经元的个数，节省存储空间并提高计算效率。
常用的汇聚方法有两种，分别是：平均汇聚和最大汇聚。
- 平均汇聚：将输入特征图划分为2×22×2大小的区域，对每个区域内的神经元活性值取平均值作为这个区域的表示；
- 最大汇聚：使用输入特征图的每个子区域内所有神经元的最大活性值作为这个区域的表示。
如图给出了两种汇聚层的示例：
汇聚层的参数量和计算量
由于汇聚层中没有参数，所以参数量为0；最大汇聚中，没有乘加运算，所以计算量为0，而平均汇聚中，输出特征图上每个点都对应了一次求平均运算。
1. 代码实现一个简单的汇聚层。
2. torch.nn.MaxPool2d()；torch.nn.avg_pool2d()代码实现
3. 比较自定义算子和框架中的算子
代码实现：
import torch
import torch.nn as nn
class Pool2D(nn.Module):
def __init__(self, size=(2, 2), mode='max', stride=1):
super(Pool2D, self).__init__()
# 汇聚方式
self.mode = mode
self.h, self.w = size
self.stride = stride
def forward(self, x):
output_w = (x.shape[2] - self.w) // self.stride + 1
output_h = (x.shape[3] - self.h) // self.stride + 1
output = torch.zeros([x.shape[0], x.shape[1], output_w, output_h])
# 汇聚
for i in range(output.shape[2]):
for j in range(output.shape[3]):
# 最大汇聚
if self.mode == 'max':
value_m = max(torch.max(x[:, :, self.stride * i:self.stride * i + self.w, self.stride * j:self.stride * j + self.h], 3).values[0][0])
output[:, :, i, j] = torch.tensor(value_m)
# 平均汇聚
elif self.mode == 'avg':
value_m = max(torch.mean(x[:, :, self.stride * i:self.stride * i + self.w, self.stride * j:self.stride * j + self.h],
3)[0][0])
output[:, :, i, j] = torch.tensor(value_m)
return output
# 1.实现一个简单汇聚层
inputs = torch.tensor([[[[1., 2., 3., 4.], [5., 6., 7., 8.], [9., 10., 11., 12.], [13., 14., 15., 16.]]]])
pool2d = Pool2D(stride=2)
outputs = pool2d(inputs)
print("input: {}, \noutput: {}".format(inputs.shape, outputs.shape))
# 比较Maxpool2D与torch API运算结果
maxpool2d_torch = nn.MaxPool2d(kernel_size=(2, 2), stride=2)
outputs_torch = maxpool2d_torch(inputs)
# 自定义算子运算结果
print('Maxpool2D outputs:', outputs)
# torch API运算结果
print('nn.Maxpool2D outputs:', outputs_torch)
avgpool2d_torch = nn.AvgPool2d(kernel_size=(2, 2), stride=2)
outputs_torch = avgpool2d_torch(inputs)
pool2d = Pool2D(mode='avg', stride=2)
outputs = pool2d(inputs)
# 自定义算子运算结果
print('Avgpool2D outputs:', outputs)
# torch API运算结果
print('nn.Avgpool2D outputs:', outputs_torch)实现结果：
input: torch.Size([1, 1, 4, 4]),
output: torch.Size([1, 1, 2, 2])
Maxpool2D outputs: tensor([[[[ 6., 8.],
[14., 16.]]]])
nn.Maxpool2D outputs: tensor([[[[ 6., 8.],
[14., 16.]]]])
Avgpool2D outputs: tensor([[[[ 5.5000, 7.5000],
[13.5000, 15.5000]]]])
nn.Avgpool2D outputs: tensor([[[[ 3.5000, 5.5000],
[11.5000, 13.5000]]]])Process finished with exit code 0
汇聚层的参数量和计算量
由于汇聚层中没有参数，所以参数量为0；
最大汇聚中，没有乘加运算，所以计算量为0，
平均汇聚中，输出特征图上每个点都对应了一次求平均运算。
选做题
使用pytorch实现Convolution Demo
翻译图片中的内容
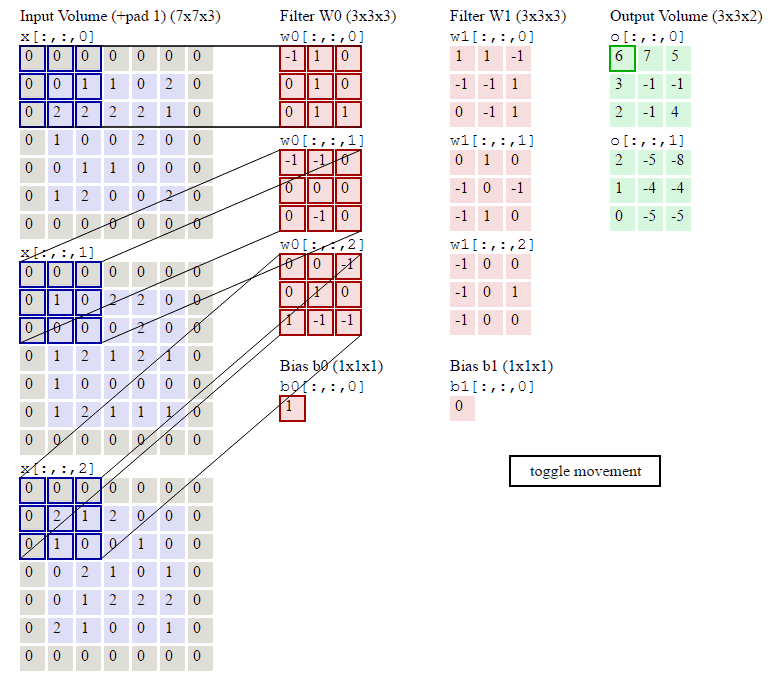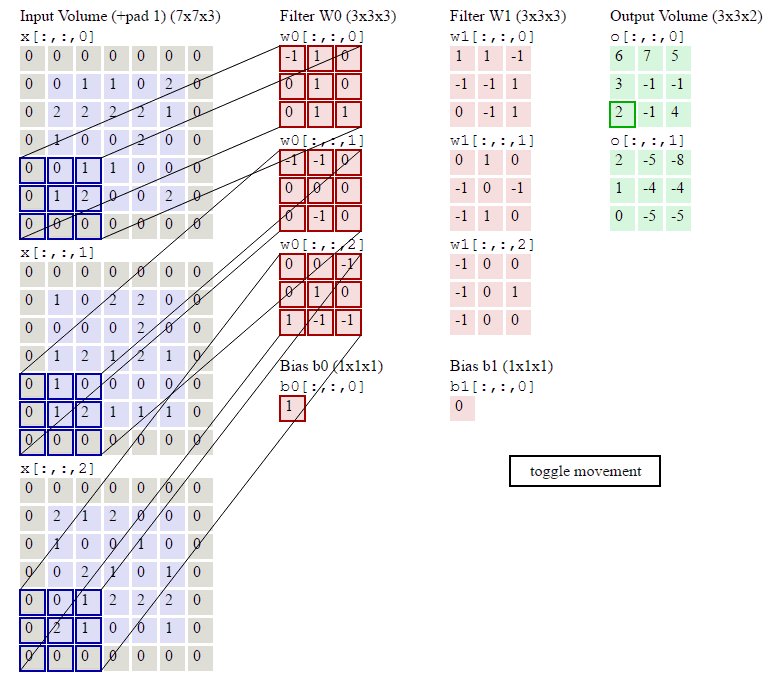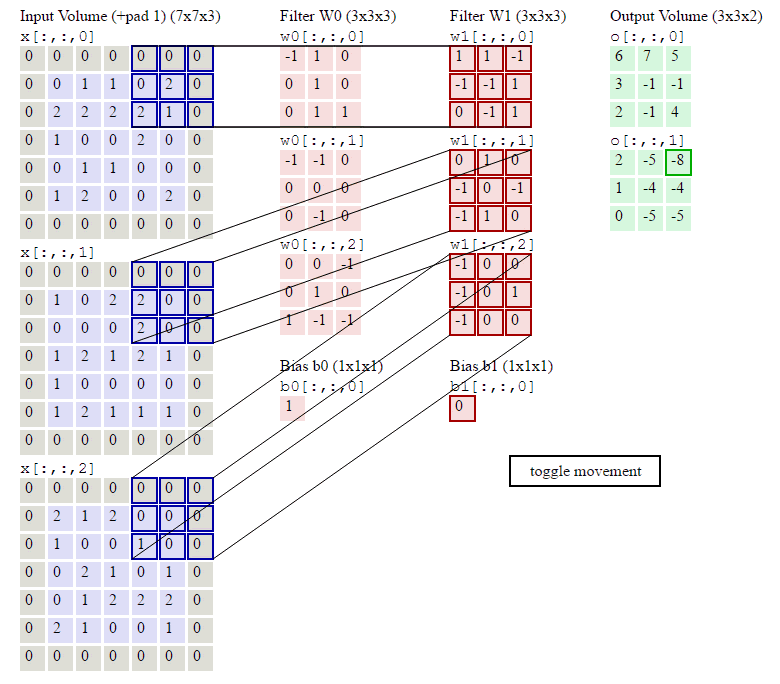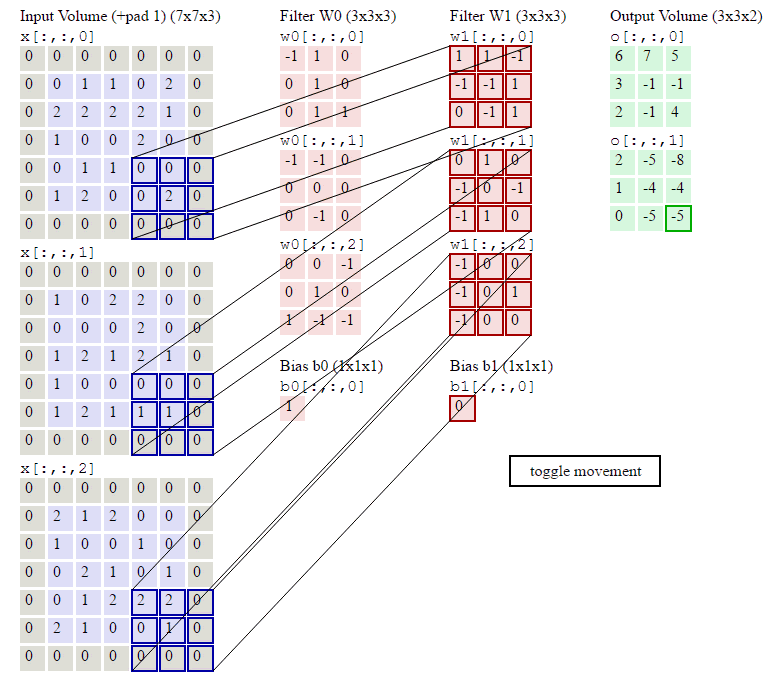
翻译：卷积演示。下面是conv层的运行演示。由于3D体积很难进行可视化，所有体积（输入体积（蓝色）、权重体积（红色）、输出体积（绿色））都会可视化，每个深度切片都会成行堆叠。输入体积的大小为
＝5，
＝5，
＝3，conv层参数为K＝2，F＝3，S＝2，P＝1。也就是说，我们有两个大小为3 X 3的过滤器，它们是应用的参数，它们是K＝2、F＝3、S＝2、P＝1的。也就是，我们有2个大小为3X 3的滤波器，它们被应用于输入体积的填充。P＝1应用于输入容积，使输入体积的外边界为零。P=1的填充应用于输入体积，使输入体积的外边界为零。将高亮显示的输入（蓝色）与过滤器（红色）按元素相乘，相加，然后将结果除以偏差。
代码实现下图
首先观察上面图片可以看出，输入的矩阵最外面一圈都是零，即可以看作是对蓝色矩阵数据进行了零填充操作，使得其尺寸变大，避免输出特征缩减，实现这个Demo即实现多通道卷积算子，只需要将对应矩阵，卷积核等参数输入即可。
实现代码：
import torch
import torch.nn as nn
class Conv2D(nn.Module):
def __init__(self, in_channels, out_channels, kernel_size, stride=1, padding=0, weight_attr=[], bias_attr=[]):
super(Conv2D, self).__init__()
self.weight = torch.nn.Parameter(weight_attr)
self.bias = torch.nn.Parameter(bias_attr)
self.stride = stride
self.padding = padding
# 输入通道数
self.in_channels = in_channels
# 输出通道数
self.out_channels = out_channels
# 基础卷积运算
def single_forward(self, X, weight):
# 零填充
new_X = torch.zeros([X.shape[0], X.shape[1]+2*self.padding, X.shape[2]+2*self.padding])
new_X[:, self.padding:X.shape[1]+self.padding, self.padding:X.shape[2]+self.padding] = X
u, v = weight.shape
output_w = (new_X.shape[1] - u) // self.stride + 1
output_h = (new_X.shape[2] - v) // self.stride + 1
output = torch.zeros([X.shape[0], output_w, output_h])
for i in range(0, output.shape[1]):
for j in range(0, output.shape[2]):
output[:, i, j] = torch.sum(new_X[:, self.stride*i:self.stride*i+u, self.stride*j:self.stride*j+v]*weight, [1, 2])
return output
def forward(self, inputs):
"""
输入：
- inputs：输入矩阵，shape=[B, D, M, N]
- weights：P组二维卷积核，shape=[P, D, U, V]
- bias：P个偏置，shape=[P, 1]
"""
feature_maps = []
# 进行多次多输入通道卷积运算
p=0
for w, b in zip(self.weight, self.bias): # P个(w,b),每次计算一个特征图Zp
multi_outs = []
# 循环计算每个输入特征图对应的卷积结果
for i in range(self.in_channels):
single = self.single_forward(inputs[:, i, :, :], w[i])
multi_outs.append(single)
# print("Conv2D in_channels:",self.in_channels,"i:",i,"single:",single.shape)
# 将所有卷积结果相加
feature_map = torch.sum(torch.stack(multi_outs), 0) + b # Zp
feature_maps.append(feature_map)
# print("Conv2D out_channels:",self.out_channels, "p:",p,"feature_map:",feature_map.shape)
p += 1
# 将所有Zp进行堆叠
out = torch.stack(feature_maps, 1)
return out
# 传入矩阵参数
Input_Volume = torch.tensor([[[0, 1, 1, 0, 2], [2, 2, 2, 2, 1], [1, 0, 0, 2, 0], [0, 1, 1, 0, 0], [1, 2, 0, 0, 2]],
[[1, 0, 2, 2, 0], [0, 0, 0, 2, 0], [1, 2, 1, 2, 1], [1, 0, 0, 0, 0], [1, 2, 1, 1, 1]],
[[2, 1, 2, 0, 0], [1, 0, 0, 1, 0], [0, 2, 1, 0, 1], [0, 1, 2, 2, 2], [2, 1, 0, 0, 1]]])
Input_Volume = Input_Volume.reshape([1, 3, 5, 5])
# 创建卷积核
# 第一层卷积核
weight_attr1 = torch.tensor([[[-1, 1, 0], [0, 1, 0], [0, 1, 1]], [[-1, -1, 0], [0, 0, 0], [0, -1, 0]],
[[0, 0, -1], [0, 1, 0], [1, -1, -1]]], dtype=torch.float32)
weight_attr1 = weight_attr1.reshape([1, 3, 3, 3])
# 第二层卷积核
weight_attr2 = torch.tensor([[[1, 1, -1], [-1, -1, 1], [0, -1, 1]], [[0, 1, 0], [-1, 0, -1], [-1, 1, 0]],
[[-1, 0, 0], [-1, 0, 1], [-1, 0, 0]]], dtype=torch.float32)
weight_attr2 = weight_attr2.reshape([1, 3, 3, 3])
# 创建偏置1，2
bias_attr1 = torch.tensor(torch.ones([3, 1]))
bias_attr2 = torch.tensor(torch.zeros([3, 1]))
# 第一层卷积的计算
conv2d_1 = Conv2D(in_channels=3, out_channels=3, kernel_size=3, stride=2, padding=1, weight_attr=weight_attr1, bias_attr=bias_attr1)
output1 = conv2d_1(Input_Volume)
print("第一层卷积,卷积核Filter W0的输出结果为:\n", output1)
# 第二层卷积的计算
conv2d_2 = Conv2D(in_channels=3, out_channels=2, kernel_size=3, stride=2, padding=1, weight_attr=weight_attr2, bias_attr=bias_attr2)
output2 = conv2d_2(Input_Volume)
print("使用卷积核Filter W1的输出结果为:\n", output2)实现结果：
第一层卷积,卷积核Filter W0的输出结果为:
tensor([[[[ 6., 7., 5.],
[ 3., -1., -1.],
[ 2., -1., 4.]]]], grad_fn=)
使用卷积核Filter W1的输出结果为:
tensor([[[[ 2., -5., -8.],
[ 1., -4., -4.],
[ 0., -5., -5.]]]], grad_fn=)
对照结果，代码实现结果与所计算的结果相同，说明实现成功。
总结
本次实验主要是对多通道卷积算子进行实现实验，以及学习汇聚层算子参数量和计算量如何计算，在对这些知识的框架进行学习后其实本次实验已经可以说是完成了，但是我个人认为最后的选做题目是十分有意义的，本次的选做相当于为前面实验学习知识的巩固所给出的一道例题，在做完选做题后，我才真正感觉掌握了这节实验的知识！
参考
魏老师，NNDL 实验六 卷积神经网络（2）基础算子
NNDL 实验5（上） - HBU_DAVID - 博客园 (cnblogs.com)