【排队论 | 数学建模常用模型】
排队论的基本概念
问题的提出
如果增添服务设备,就要增加投资或可能发生空闲浪费;如果服务设备太少,排队现象就会严重,对顾客甚至对社会都会发生不利影响。因此,管理人员必须考虑如何在这两者之间取得平
衡,以提高服务质量,降低成本。
排队论研究内容*
排队论(queuing theory)也称随机服务系统理论,是为研究和解决具有拥挤现象的问题而发展起来的一门应用数学的分支,其研究内容包括三个部分:
- 性态问题:即研究各种排队系统的概率规律性,主要是研究队长分布、等待时间分布和忙期分布等,包括了瞬态和稳态两种情形。
- 最优化问题
静态最优 >>最优设计
动态最优>>最优运营 - 统计推断问题:判断排队系统的类型
①一般表示
- 各个顾客由顾客源(总体)出发,到达服务机构(服务台、服务员)前排队等候接受服务,服务完成后离开。
- 排队结构指队列的数目和排列方式,排队规则和服务规则是说明顾客在排队系统中按怎样的规则、次序接受服务的。
一个排队系统包括
- 在一定时间内顾客平均到达多少?
- 按什么规律到达(输入过程服从什么分布)?
- 进入系统的顾客按照什么规则排队?
- 服务机构设置多少服务设施?排列形式?
- 服务时间服从什么分布?
服务机构*





排队系统的(三大)组成和特征*
输入过程
- 顾客总体:有限,无限。
- 顾客到达方式:单个,成批。
- 顾客到达间隔时间:确定的、随机的。
- 顾客到达的独立性:独立,不独立。
- 输入过程的平稳性:与时间无关(平稳的),与时间有关(非平稳的)。
排队及排队规则
- 即时制(损失制)
- 等待制
- 先到先服务:FCFS
- 后到先服务:LCFS
- 随机服务:SIRO
- 优先权服务:PR
- 队容量:有限,无限;有形,无形。
- 队列数目:单列,多列。
服务机构
- 服务员数量:无,单个,多个。
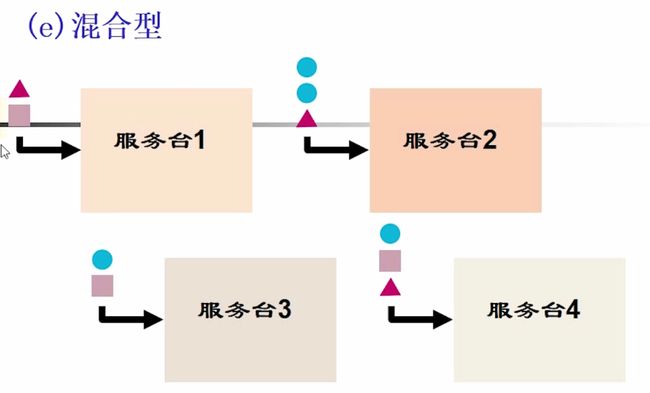
- 队列与服务台的组合
- 服务方式:单个顾客,成批顾客。
- 服务时间:确定的,随机的。服务时间和到达间隔时间至少一个是随机的。
- 服务时间分布是平稳的。
排队论的基本分布
排队论中的常见分布:泊松分布、指数分布与爱尔朗分布_Norstc的博客-CSDN博客_erlang分布
排队系统的分类*
运筹学-排队论(学习笔记) - 知乎 (zhihu.com)
一般可以用6个特征来表示一个排队模型,即 X / Y / Z / A / B / C X/Y/Z/A/B/C X/Y/Z/A/B/C
原则
X : X: X: 相继到达的间隔时间的分布,一般为负指数分布
Y : Y: Y:服务时间的分布,一般为负指数分布或者确定性
Z : Z: Z:服务台的数目,1台或者多台
A : A: A:系统客量的限制,系统中是否存在顾客的最大数量限制
B : B: B:顾客源数目,顾客源是否有限
C : C: C:服务规则,先到先服务或者后到先服务等
注:在本节中仅考虑先到先服务,因此省略最后一个特征服务规则
其中常用符号有:
M : M: M:负指数分布
D : D: D:确定型
E k : k E_k:k Ek:k阶爱尔朗分布
G : G: G: 一般服务时间分布
如标准 M / M / 1 / ∞ / ∞ M/M/1/\infty/\infty M/M/1/∞/∞ 模型表示:输入过程服从泊松分布,服务时间服从负指数分布,系统容量无限制且顾客源无限的模型
常用指标*
-
队长: L s Ls Ls:Length of System 指系统内顾客数目
-
排队长: L q Lq Lq:length of qeuen 指排队中的顾客数目
-
系 统 内 顾 客 数 目 ( L s ) = 排 队 中 顾 客 数 目 ( L q ) + 正 在 接 受 服 务 的 顾 客 数 目 系统内顾客数目(Ls)=排队中顾客数目(Lq)+正在接受服务的顾客数目 系统内顾客数目(Ls)=排队中顾客数目(Lq)+正在接受服务的顾客数目
-
逗留时间: W s Ws Ws:逗留时间指顾客在排队服务系统中从进入到服务完毕离去的平均逗留时间,期望值记作 W s Ws Ws
-
等待时间: W q Wq Wq:等待时间指顾客排队等待服务的平均等待时间,期望值记作 W q Wq Wq
-
忙期:从顾客到达空闲服务机构起到服务机构再次为空闲这段时间的长度,即服务机构连续繁忙的时间长度,它关系到服务员的工作强度。忙期和一个忙期中平均完成服务顾客数都是衡量服务机构效率的指标。
-
损失率
-
服务强度
系统状态的概率分布*
在时刻 t t t,系统状态为 n n n的概率可以表示为 P n ( t ) P_n(t) Pn(t)
例题
M/M/1模型
某修理店只有一个修理工人,来修理的顾客到达次数服从Poisson分布,平均每小时3人,修理时间服从负指数分布,平均需10m分钟,求
- 修理店空闲时间概率
- 店内有四个顾客的概率
- 店内至少有一个顾客的概率
- 在店内顾客的平均数
- 等待服务的顾客平均数
- 在店内平均逗留时间
- 平均等待修理时间
如果到达次数服从Poission分布,那么到达间隔时间服从负指数分布
负指数分布(密度函数为 λ e − λ t \lambda e^{-\lambda t} λe−λt)与输入过程为泊松分布是等价的
M(负指数分布,具有无记忆性)
λ \lambda λ:单位时间平均到达顾客数
1 λ \frac{1}{\lambda} λ1:相继顾客到达平均时间
μ \mu μ:单位时间内受到服务的顾客平均数
v v v:服务时间,也就是相继离开系统的两顾客的间隔时间
ρ = λ μ \rho=\frac{\lambda}{\mu} ρ=μλ: ρ \rho ρ代表服务强度
1.修理店空闲时间概率
λ = 3 μ = 60 / 10 = 6 ρ = λ μ = 3 6 = 1 2 P 0 = 1 − ρ = 1 2 \lambda=3 \\ \mu=60/10=6 \\ \rho=\frac{\lambda}{\mu}=\frac{3}{6}=\frac{1}{2} \\ P_0=1-\rho=\frac{1}{2} λ=3μ=60/10=6ρ=μλ=63=21P0=1−ρ=21
2.店内有四个顾客的概率
P 4 = ( 1 − ρ ) ρ 4 = 1 32 P_4=(1-\rho){\rho}^4=\frac{1}{32} P4=(1−ρ)ρ4=321
3.店内至少有一个顾客的概率
P ( n ≥ 1 ) = 1 − P 0 = 1 2 P(n \ge 1)=1-P_0=\frac{1}{2} P(n≥1)=1−P0=21
4.在店内顾客的平均数
L s = ∑ n = 0 ∞ n ⋅ P n = ∑ n = 0 ∞ n ( 1 − ρ ) ρ n = ( 1 − ρ ) ρ + 2 ( 1 − ρ ) ρ 2 + 3 ( 1 − ρ ) ρ 3 + 4 ( 1 − ρ ) ρ 4 + . . . = ( ρ − ρ 2 ) + ( 2 ρ 2 − 2 ρ 3 ) + ( 3 ρ 3 − 3 ρ 4 ) + ( 4 ρ 4 − 4 ρ 5 ) + . . . = ρ + ρ 2 + ρ 3 + ρ 4 = ρ 1 − ρ \begin{array}{l} Ls = \sum_{n = 0}^{\infty } n \cdot P_n \\= \sum_{n = 0}^{\infty }n (1-\rho){\rho}^n \\= (1-\rho){\rho}+2(1-\rho){\rho}^2+3(1-\rho){\rho}^3+4(1-\rho){\rho}^4+... \\=({\rho}-{\rho}^2)+(2{\rho}^2-2{\rho}^3)+(3{\rho}^3-3{\rho}^4)+(4{\rho}^4-4{\rho}^5)+... \\={\rho}+{\rho}^2+{\rho}^3+{\rho}^4 \\=\frac{\rho}{1-\rho} \end{array} Ls=∑n=0∞n⋅Pn=∑n=0∞n(1−ρ)ρn=(1−ρ)ρ+2(1−ρ)ρ2+3(1−ρ)ρ3+4(1−ρ)ρ4+...=(ρ−ρ2)+(2ρ2−2ρ3)+(3ρ3−3ρ4)+(4ρ4−4ρ5)+...=ρ+ρ2+ρ3+ρ4=1−ρρ
L s = ρ 1 − ρ = 1 2 1 − 1 2 = 1 Ls=\frac{\rho}{1-\rho}=\frac{\frac{1}{2}}{1-\frac{1}{2}}=1 Ls=1−ρρ=1−2121=1
5.等待服务的顾客平均数
L q = ∑ n = 1 ∞ ( n − 1 ) ⋅ P n = p 2 + 2 p 3 + 3 p 4 + 4 p 5 + ⋯ = ( 1 − ρ ) ρ 2 + 2 ( 1 − ρ ) ρ 3 + 3 ( 1 − ρ ) ρ 4 + 4 ( 1 − ρ ) ρ 5 + ⋯ = ρ 2 − ρ 3 + 2 ρ 3 − 2 ρ 4 + 3 ρ 4 − 3 ρ 5 + 4 ρ 5 − 4 ρ 6 + ⋯ = ρ 2 + ρ 3 + ρ 4 + ρ 5 + . . . = ρ 2 1 − ρ \begin{array}{l} Lq=\sum_{n=1}^{\infty}(n-1) \cdot P_{n} \\=p_{2}+2 p_{3}+3 p_{4}+4 p_{5}+\cdots \\=(1-\rho) {\rho}^{2}+2(1-\rho) \rho^{3}+3(1-\rho) \rho^{4}+4(1-\rho) \rho^{5}+\cdots \\=\rho^{2}-\rho^{3}+2 \rho^{3}-2 \rho^{4}+3 \rho^{4}-3 \rho^{5}+4 \rho^{5}-4 \rho^{6}+\cdots \\={\rho}^2+{\rho}^3+{\rho}^4+{\rho}^5+... \\=\frac{\rho^2}{1-\rho} \end{array} Lq=∑n=1∞(n−1)⋅Pn=p2+2p3+3p4+4p5+⋯=(1−ρ)ρ2+2(1−ρ)ρ3+3(1−ρ)ρ4+4(1−ρ)ρ5+⋯=ρ2−ρ3+2ρ3−2ρ4+3ρ4−3ρ5+4ρ5−4ρ6+⋯=ρ2+ρ3+ρ4+ρ5+...=1−ρρ2
L q = ρ 2 1 − ρ = ( 1 2 ) 2 1 − 1 2 = 1 2 Lq=\frac{\rho^2}{1-\rho}=\frac{(\frac{1}{2})^2}{1-\frac{1}{2}}=\frac{1}{2} Lq=1−ρρ2=1−21(21)2=21
6.在店内平均逗留时间
设该顾客到达时已经有n位顾客,按照先到先服务的规则,该顾客在系统中的逗留时间
W n = T 1 ′ + T 2 + ⋯ + T n + T n + 1 W_{n}=T_{1}^{\prime}+T_{2}+\cdots+T_{n}+T_{n+1} Wn=T1′+T2+⋯+Tn+Tn+1
T 1 ′ T_{1}^{\prime} T1′为正在被服务的第1位顾客需要的服务时间;
T i ( i − 2 , . . . , n + 1 ) T_i(i-2,...,n+1) Ti(i−2,...,n+1)独立且同分布,均为参数为 μ \mu μ的负指数分布, T 1 ′ T_{1}^{\prime} T1′由于无记忆性,也服从参数为 μ \mu μ的负指数分布,从而 W n W_n Wn服从 ( n + 1 ) (n+1) (n+1)阶爱尔朗分布
f W n ( t ) = μ ( μ t ) n n ! e − μ t t ⩾ 0 f_{W_{n}(t)}=\frac{\mu(\mu t)^{n}}{n !} e^{-\mu t} \quad t \geqslant 0 fWn(t)=n!μ(μt)ne−μtt⩾0
F ( t ) = p ( W ⩽ t ∣ n ) = ∑ n = 0 ∞ p n ⋅ p ( W ⩽ t ∣ n ) = ∑ n = 0 ∞ ( 1 − e ) e n ⋅ ∫ 0 t μ ( μ t ) n n ! e − μ t d t = 1 − e − ( μ − λ ) t t ≥ 0 \begin{array}{l} F(t)=p(W \leqslant t | n) & \\=\sum_{n=0}^{\infty} p_{n} \cdot p(W \leqslant t \mid n) \\=\sum_{n=0}^{\infty}(1-e) e^{n} \cdot \int_{0}^{t} \frac{\mu(\mu t)^{n}}{n !} e^{-\mu t} d t \\=1-e^{-(\mu-\lambda) t} \quad t \ge 0 \end{array} F(t)=p(W⩽t∣n)=∑n=0∞pn⋅p(W⩽t∣n)=∑n=0∞(1−e)en⋅∫0tn!μ(μt)ne−μtdt=1−e−(μ−λ)tt≥0
所以 W W W服从参数为 μ \mu μ的负指数分布
f ( t ) = ( μ − λ ) e − ( μ − λ ) t ≥ 0 f(t)=(\mu - \lambda)e^{-(\mu - \lambda)t} \quad \ge 0 f(t)=(μ−λ)e−(μ−λ)t≥0
W s = 平 均 逗 留 时 间 = 1 μ − λ = 1 6 − 3 = 1 3 小 时 = 20 分 钟 \begin{array}{l} Ws=平均逗留时间 \\=\frac{1}{\mu - \lambda} \\=\frac{1}{6-3} \\=\frac{1}{3}小时 \\=20分钟 \end{array} Ws=平均逗留时间=μ−λ1=6−31=31小时=20分钟
7.平均等待修理时间
W q = W s − E V = W s − 1 μ = 1 6 − 3 − 1 6 = 1 6 小 时 \begin{aligned} W_{q} &=W_{s}-E V \\ &=W_{s}-\frac{1}{\mu} \\ &=\frac{1}{6-3}-\frac{1}{6} \\ &=\frac{1}{6}小时 \end{aligned} Wq=Ws−EV=Ws−μ1=6−31−61=61小时





