Day02-《西瓜书》-线性模型(DataWhale)
三、线性模型
出处: Datawhale吃瓜教程(https://www.bilibili.com/video/BV1Mh411e7VU)
具有很好的可解释性(comprehensibility)
机器学习三要素:
- 模型:根据具体问题,确定假设空间
- 策略:根据评估标准,确定选取最优模型的策略(通常会产生一个“损失函数”)
- 算法:求解损失函数,确定最优模型
3.1 基本形式
给定d个属性描述的示例 x = ( x 1 , x 2 , . . . , x d ) \mathbf{x}=(x_1,x_2,...,x_d) x=(x1,x2,...,xd)
线性模型:
f ( x ) = ω 1 x 1 + ω 2 x 2 + . . . + ω d x d + b f(x)=\omega_1x_1+\omega_2x_2+...+\omega_dx_d+b f(x)=ω1x1+ω2x2+...+ωdxd+b
一般形式:
f ( x ) = ω T x + b f(x) = \omega^T\mathbf{x}+b f(x)=ωTx+b
其中: ω = ( ω 1 , ω 2 , . . . , ω d ) \omega=(\omega_1,\omega_2,...,\omega_d) ω=(ω1,ω2,...,ωd), ω \omega ω和 b b b 学得后,模型确定。
3.2 线性回归
给定数据集 D = { ( x 1 , y 1 ) , ( x 2 , y 2 ) , . . . , ( x m , y m ) } D=\{(\mathbf{x_1},y_1),(\mathbf{x_2},y_2),...,(\mathbf{x_m},y_m)\} D={(x1,y1),(x2,y2),...,(xm,ym)}, x i = ( x i 1 , x i 2 , . . . , x i d ) , y ∈ R \mathbf{x_i}=(x_{i1},x_{i2},...,x_{id}),y\in \mathbb R xi=(xi1,xi2,...,xid),y∈R
3.2.1 一元线性回归
f ( x i ) = ω x i + b f(x_i) = \omega x_i+b f(xi)=ωxi+b
使得 f ( x i ) ≈ y i f(x_i)\approx y_i f(xi)≈yi。
如何确定 ω \omega ω和 b b b:
试图将均方误差(对应欧式距离)最小化
E ( ω , b ) = ( ω ∗ , b ∗ ) = a r g m i n ( ω , b ) ∑ i = 1 m ( f ( x i ) − y i ) 2 = a r g m i n ( ω , b ) ∑ i = 1 m ( y i − ω x i − b ) 2 \begin{aligned} E_{(\omega,b)}=(\omega ^*,b^*) &= \mathop{argmin}_{(\omega,b)}\sum_{i=1}^m(f(x_i)-y_i)^2\\ &= \mathop{argmin}_{(\omega,b)}\sum_{i=1}^m(y_i-\omega x_i-b)^2 \end{aligned} E(ω,b)=(ω∗,b∗)=argmin(ω,b)i=1∑m(f(xi)−yi)2=argmin(ω,b)i=1∑m(yi−ωxi−b)2
E ( ω , b ) E(\omega,b) E(ω,b)是关于 ω \omega ω 和 b b b 的凸函数,当它关于 ω \omega ω 和 b b b 的导数均为0时,得到最优解。
最终求得的 ω \omega ω 和 b b b为:
ω = ∑ i = 1 m y i ( x i − x ‾ ) ∑ i = 1 m x i 2 − 1 m ( ∑ i = 1 m x i ) 2 b = y ‾ − ω x ‾ \begin{aligned} \omega &= \frac{\sum_{i=1}^{m}y_i(x_i-\overline{x})}{\sum_{i=1}^mx_i^2-\frac{1}{m}(\sum_{i=1}^mx_i)^2} \\ \\ b &=\overline{y}-\omega \overline{x} \end{aligned} ωb=∑i=1mxi2−m1(∑i=1mxi)2∑i=1myi(xi−x)=y−ωx
凸函数:https://zhuanlan.zhihu.com/p/56876303
凸函数:
- 定义
- 对区间[a,b]上定义的函数 f f f,若在区间中任意两点 x 1 , x 2 x_1,x_2 x1,x2 均有 f ( x 1 + x 2 2 ) ≤ f ( x 1 ) + f ( x 2 ) 2 f(\frac{x_1+x_2}{2})\le \frac{f(x_1)+f(x_2)}{2} f(2x1+x2)≤2f(x1)+f(x2),则称 f f f为区间[a,b]上的凸函数
- 对实数集上的函数,若二阶导数在区间上非负,则是凸函数;若二阶导数恒大于0,则严格凸函数
- 优点
- 有利于求最小化问题。凸函数只有一个极小值,也就是最小值
- 常见凸函数
- 指数函数: e a x \mathcal{e}^{ax} eax
- 幂函数: x a x^a xa,当 a ≥ 1 a\ge 1 a≥1 or a < 0 a<0 a<0时
- 负熵函数: x l o g ( x ) xlog(x) xlog(x)
2.3.2 多元线性回归
样本由d个属性描述,
f ( x i ) = ω T x i + b f(\mathbf{x_i})=\omega ^T\mathbf{x_i}+b f(xi)=ωTxi+b
使用最小二乘对 ω \omega ω 和 b 进行估计
最终求得的 ω \omega ω:
ω ^ = ( X T X ) − 1 X T y \hat{\omega} = (X^TX)^{-1}X^Ty ω^=(XTX)−1XTy
推导过程:
3.3 对数几率回归(逻辑回归)
三要素:
- 模型:线性模型,输出值的范围为[0,1],近似阶跃的单调可微函数
- 策略:极大似然估计,信息论
- 算法:梯度下降,牛顿法
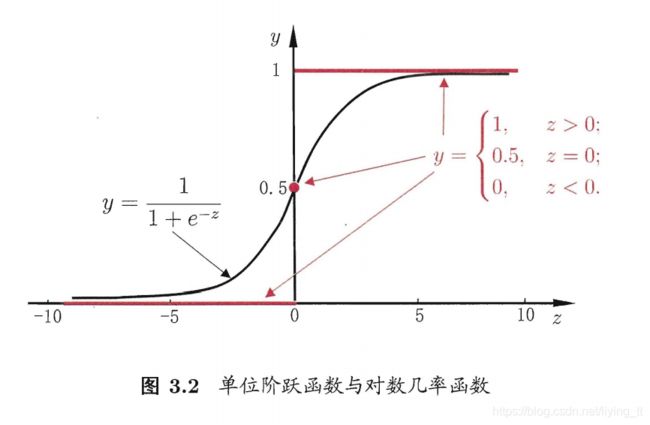
考虑二分类任务,输出标记 y ∈ 0 , 1 y \in {0,1} y∈0,1,而线性回归模型产生的而预测值 z = ω T x + b z=\omega^Tx+b z=ωTx+b是实值。考虑将实值 z z z转换为0/1值。最理想的是“单位阶跃函数”(unit-step function)
y = { 0 , z < 0 0.5 , z = 0 1 , z > 0 y = \begin{cases} \begin{aligned} 0,z&<0\\ 0.5,z&=0 \\ 1,z&>0 \end{aligned} \end{cases} y=⎩⎪⎨⎪⎧0,z0.5,z1,z<0=0>0
即预测值z大于0判为正例,小于0判为反例,预测值为临界值零则可任意判别。
但是单位阶跃函数不连续,使用对数几率函数(logistic function)进行替代。
y = 1 1 + e − z y = \frac{1}{1+e^{-z}} y=1+e−z1
最优解为:
β ∗ = a r g m i n β l ( β ) \beta^* = \mathop{argmin}_{\beta}{l}(\beta) β∗=argminβl(β)
使用牛顿法,其第t+1轮迭代解的更新公式为:
β t + 1 = β t − ( ∂ 2 l ( β ) ∂ β ∂ β T ) − 1 ∂ l ( β ) ∂ β \beta ^{t+1} = \beta^t-(\frac{\partial^2l(\beta)}{\partial\beta \partial\beta^T})^{-1}\frac{\partial l(\beta)}{\partial \beta} βt+1=βt−(∂β∂βT∂2l(β))−1∂β∂l(β)
其中, β \beta β的一阶、二阶导数分别为:
∂ l ( β ) ∂ β = − ∑ i = 1 m x i ^ ( y i − p 1 ( x i ^ ; β ) ) ∂ 2 l ( β ) ∂ β ∂ β T = ∑ i = 1 m x i ^ x i ^ T p 1 ( x i ^ ; β ) ( 1 − p 1 ( x i ^ ; β ) ) \begin{aligned} \frac{\partial l({\beta})}{\partial \beta} &= -\sum_{i=1}^{m}\hat{x_i}(y_i-p_1(\hat{x_i};\beta))\\ \frac{\partial ^2l(\beta)}{\partial \beta \partial \beta^T} &= \sum_{i=1}^m\hat{x_i}\hat{x_i}^Tp_1(\hat{x_i};\beta)(1-p_1(\hat{x_i};\beta)) \end{aligned} ∂β∂l(β)∂β∂βT∂2l(β)=−i=1∑mxi^(yi−p1(xi^;β))=i=1∑mxi^xi^Tp1(xi^;β)(1−p1(xi^;β))
推导:
3.4 线性判别分析
(Linear Discriminant Analysis,LDA)
思想:给定训练样例,将样例投影到一条直线上,使同类样例的投影点尽可能接近、异类样例的投影点尽可能远离;在对新样本进行分类时,将其投影到同样的这条直线上,再根据投影点的位置来确定新样本的类别。