布隆过滤器以及python实现
文章目录
- 什么是布隆过滤器
-
- 工作原理
- python实现
在开发以及数据处理过程中,我们经常要判断一个元素是否在一个集合中,或者对一批元素去重,最直接的办法是是将所有元素存在计算机中,遇到新的元素时,将它和集合中的元素比较即可,当集合小时这样做快速准确,但当集合规模巨大时,因为要耗费存储空间,其存储效率低的问题的就显现出来。今天介绍一种数学工具来解决大集合的过滤问题——布隆过滤器
什么是布隆过滤器
布隆过滤器(Bloom Filter)是由伯顿·布隆(Burton Bloom)于1970年提出的。实际上是一个很长的二进制向量和一系列随机映射函数。可以用来告诉你 “某样东西一定不存在或者可能存在”。
工作原理
假定存储一亿个元素,先建立一个16亿个比特位即2亿字节的向量,然后将这16亿个比特位全部清零。对于每一个元素X,用8个不同的随机数产生器(F1,F2,···,F8)产生8个信息指纹(f1,f2,···,f8),再将这8个信息指纹映射到1-16亿中的8个自然数g1,g2,···,g8。现在将这8个位置的比特位全部设置为1。对这一亿个元素都进行这样的处理后,一个针对这些元素的布隆过滤器就建成了,如下图:
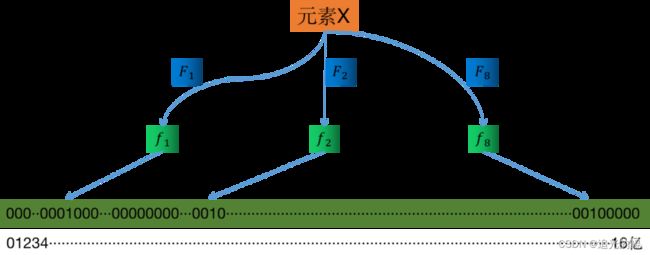
现在,来了一个新的元素Y,判断这个元素在不在过滤器中。用相同的8个随机数生成器产生8个信息指纹,然后对应到布隆过滤器的8个比特位,如果Y在过滤器中,显然,其对应的8个比特值一定是1,如果对应的8个比特值不全是1,那么Y一定不在过滤器中。
布隆过滤器判断一个元素不存在,那么一定不存在。但是,他有个不足之处,即有极小的可能将一个不存在的元素判定为存在,因为可能某个不存在的元素在布隆过滤器中对应的8个位置“恰巧”被其他元素设置成1,我们把这种可能性称为误识别率。
这里有三个相关的推导公式用,假设需要过滤的元素个数为n,布隆过滤器的大小为m,所容忍的误识别率为p,随机数生成器(哈希函数)的个数为k。公式如下(小数向上取整):
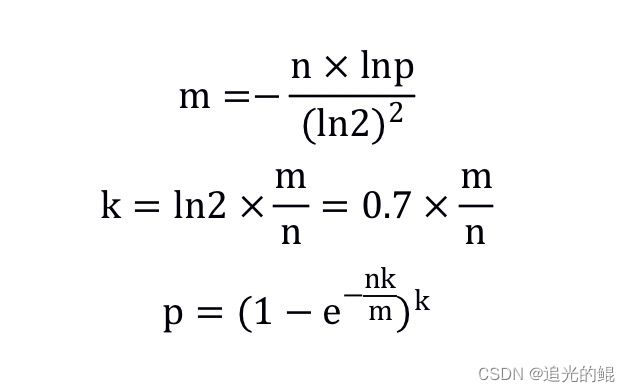
由于我们计算的m和k可能是小数,那么需要经过向上取整,此时需要重新计算误判率p!
python实现
通过python实现可以有两种方式:1、布隆过滤器直接用内存存储;2、布隆过滤器用redis存储。用redis实现可以支持并发,多进程过滤。
我们先创建一个布隆过滤器的基类如下:
import math
class BloomFilter(object):
def __init__(self, capacity=10000000, error_rate=0.0000001):
"""
布隆过滤器
:param capacity: 是预先估计要去重的数量
:param error_rate: 接受的误识别率
· m: 需要的总bit位数
· k: 需要最少的hash次数
· p: 实际的错误率(因向上取整)
· mem: 需要的多少M内存
"""
self.m = math.ceil(-(capacity * math.log(error_rate) / pow(math.log(2), 2)))
self.k = math.ceil(math.log(2) * self.m / capacity)
self.p = pow((1 - pow(math.e, -(capacity * self.k) / self.m)), self.k)
self.mem = math.ceil(self.m / 8 / 1024 / 1024)
def add(self, value):
"""
向布隆过滤器中添加一个元素
:param value: 要加入过滤器的元素
:return:
"""
raise Exception("为实现的方法")
def is_exist(self, value):
"""
判断一个元素是否存在
:param value: 待判断的元素
:return: 布尔
"""
raise Exception("为实现的方法")
def get_hashes(self, value):
"""
获取hash值
:param value: 需要进行hash的元素
:return: list, self.k次hash值对应布隆过滤器的位数
"""
raise Exception("为实现的方法")
一个布隆过滤器应该包括代码中的这些属性,以及添加、判断是否存在、获取hash值这些方法。这些方法的具体实现不同的版本有所不同。我们先来看基于内存的实现,其中用到了mmh3和bitarray包。
import mmh3
from bitarray import bitarray
class RAMBloomFilter(BloomFilter):
# 内置100个随机种子
SEEDS = [543, 460, 171, 876, 796, 607, 650, 81, 837, 545, 591, 946, 846, 521, 913, 636, 878, 735, 414, 372,
344, 324, 223, 180, 327, 891, 798, 933, 493, 293, 836, 10, 6, 544, 924, 849, 438, 41, 862, 648, 338,
465, 562, 693, 979, 52, 763, 103, 387, 374, 349, 94, 384, 680, 574, 480, 307, 580, 71, 535, 300, 53,
481, 519, 644, 219, 686, 236, 424, 326, 244, 212, 909, 202, 951, 56, 812, 901, 926, 250, 507, 739, 371,
63, 584, 154, 7, 284, 617, 332, 472, 140, 605, 262, 355, 526, 647, 923, 199, 518]
def __init__(self, capacity=10000000, error_rate=0.000001):
super().__init__(capacity, error_rate)
self.seeds = self.SEEDS[0:self.k]
self.bloom = bitarray(self.m)
self.bloom.setall(0)
def add(self, value):
hashes = self.get_hashes(value)
for index in hashes:
self.bloom[index] = 1
def is_exist(self, value):
hashes = self.get_hashes(value)
exist = True
for index in hashes:
exist = exist & self.bloom[index]
return exist
def get_hashes(self, value):
hashes = []
for seed in self.seeds:
hash = mmh3.hash(value, seed)
hashes.append(hash % self.m)
return hashes
其中内置的随机种子保证同一个value,经多次hash后得到的位数(布隆过滤器的index)不变。接下来我们看看基于redis的实现。
import redis
class RedisBloomFilter(BloomFilter):
# 内置100个随机种子
SEEDS = [543, 460, 171, 876, 796, 607, 650, 81, 837, 545, 591, 946, 846, 521, 913, 636, 878, 735, 414, 372,
344, 324, 223, 180, 327, 891, 798, 933, 493, 293, 836, 10, 6, 544, 924, 849, 438, 41, 862, 648, 338,
465, 562, 693, 979, 52, 763, 103, 387, 374, 349, 94, 384, 680, 574, 480, 307, 580, 71, 535, 300, 53,
481, 519, 644, 219, 686, 236, 424, 326, 244, 212, 909, 202, 951, 56, 812, 901, 926, 250, 507, 739, 371,
63, 584, 154, 7, 284, 617, 332, 472, 140, 605, 262, 355, 526, 647, 923, 199, 518]
def __init__(self, capacity=10000000, error_rate=0.000001, redis_conf=None, redis_key=""):
super().__init__(capacity, error_rate)
self.seeds = self.SEEDS[0:self.k]
self.redis_key = redis_key
pool = redis.ConnectionPool(**redis_conf)
self.bloom = redis.StrictRedis(connection_pool=pool)
if not self.bloom.exists(redis_key):
self.bloom.setbit(self.redis_key, self.m - 1, 0)
def add(self, value):
hashes = self.get_hashes(value)
for index in hashes:
self.bloom.setbit(self.redis_key, index, 1)
def is_exist(self, value):
hashes = self.get_hashes(value)
exist = True
for index in hashes:
exist = exist & self.bloom.getbit(self.redis_key, index)
return exist
def get_hashes(self, value):
hashes = []
for seed in self.seeds:
hash = mmh3.hash(value, seed)
hashes.append(hash % self.m)
return hashes
以上只是实现了布隆过滤器的基本方法,而且完全可以在一个类中支持基于内存和基于redis两种模式。在实际生产中,还有一些其他问题在代码中没有实现,比如:为了避免误判而设置的白名单;清除已存的过滤器重新添加或者接着在已有的过滤器上添加等。
最后,建议在使用布隆过滤器之前,根据应用场景先评估一下需要的存储空间,hash次数等,调整可接受的误判率。