基于遗传算法对旅行商问题的求解

遗传算法求解TSP问题的计算机仿真绪论

由于遗传算法在整体搜索策略和优化搜索方法上不依赖梯度信息或其他辅助知识,只需要影响搜索方向的目标函数和相应的适应度函数,所以提供了一种求解复杂系统问题的通用框架,因此遗传算法广泛应用于数学问题、组合优化、机械设计、人工智能等领域。遗传算法( Genetic Algorithms,简称GA)是模拟自然界生物自然选择和进化的机制而发展起来的一种高度并行、自适应的随机搜索算法。特别适合于求解传统的搜索算法不好处理的复杂的最优解问题。旅行商问题( Traveling Salesman Problem)就是要决定条经过路线中所有城市当且仅当一次且距离最短的路线,即距离最短的 Hamilton回路。旅行商问题是一个具有十分广泛的实用背景和重要理论价值的组合优化问题。目前求解TSP问题的主要方法有模拟退火算法、遗传算法、 Hopfield神经网络算法、启发式搜索法、二叉树描述算法。本文选用遗传算法求解2个和50个城市的TSP问题,基于MATLAB,通过多次的迭代近似的求解出了行走的最优解,最终实现了计算机仿真求解TSP问题。

研究背景

旅行商问题（TSP）也称为旅行推销员问题，具体的模型可以这样理解：现在给定N个城市之间的位置；旅行商从其中一个城市出发，不重复访问每一个城市，最终又返回到原来的初始城市，要求我们找到这样的一条曲线，使得旅行商所走的路程最短。如果我们采用遍历的方法解决则有N!中可能性，这样一个NP问题，一般的求解方法都会产生巨大的复杂度。但是随着智能优化算法的出现，使得解决这种NP问题可以在一定的迭代后得到一个比较满意的结果。该类算法可以处理传统搜索方法但是难以解决的复杂和非线性问题，现如今已经广泛的应用到人工智能、机械设计、自适应控制的领域。在这次实验作业中将使用遗传优化算法来解决TSP问题。
程序设计思路和设计方法

1. 对于TSP问题下设计的遗传优化算法

1.1 对解空间进行编码，每一个个体就是一个解空间，对于TSP问题来说每一个个体就是对N进行一次permution。得到一次走完一圈的路径。
1.2 初始化并且设置相关参数。在遗传算法中要设置最大迭代的代数G以及种群个数NP以及当前迭代次数gen。对于初始化来说就是对这NP个个体进行编码，得到初始的种群解空间。
1.3 适应度计算。在该问题中适应度就是走一圈所需要的长度。并且记录当前最优的适应度和适应度的平均值。
1.4 选择优良个体并且进行交叉和变异操作：通过1.3产生了适应度，排序，选择前P个个体。然后使用交叉算子交换任意两个个体的基因达到更改个体路径的目的。接下来进行变异操作，任意选择个体，用随机法交换两个基因的位置，通过这种类似于的变异的方法也可以产生新的路径。
1.5 产生新的种群。将父代和交叉得到的以及变异得到的个体重新计算适应度函数，并且排序，取出前NP个个体作为新一轮的种群。
1.6 Gen++,若gen < Z则返回到1.3。不满足此不等式则程序结束转入1.7。
1.7 可视化运行结果图以及行走路线。
2. 程序流程图如下图所示：

3.模型验证和性能检验（参数，运行时间）

1. 首先我们检验了当城市数N为25时改遗传优化算法相关性能。(距离矩阵是随机数产生的)
   城市个数 最大迭代次数G 种群大小NP 程序运行时间 最短距离
   25 100 50 0.1581s 5039.2
   25 100 100 0.1067s 6003.9
   25 100 200 0.1909s 5687.5
   25 200 50 0.0916s 4643.6
   25 200 100 0.1514s 5340.5
   25 200 200 0.2916s 5179.4
   经历这两个参数6中组合的模型结果来看程序的运行时间相差都不是很大可以接受，所以我们主要将注意力放到最短的距离上如图所得当G = 200,NP = 50时有最短的距离，所以在该种参数组合下将上述的参数组合作为最优的参数组合并可视化结果：
   
   

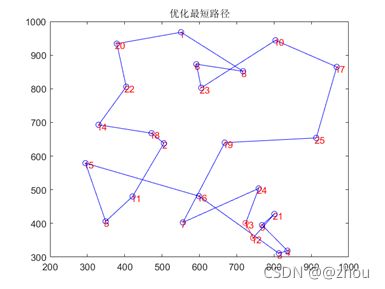
由适应度进化曲线可知随着迭代次数的增加，其每轮的最优适应度是稳定的，根据此图从侧面也反映了我们的遗传算法是比较正确的。
2. 在测试了城市个数为25的基础上我们增加一倍现在将城市个数设置为N = 50，再次进行计算机求解看在城市个数翻倍情况下运行时间。
城市个数 最大迭代次数G 种群大小NP 程序运行时间 最短距离
50 100 50 0.1394s 12519
50 100 100 0.1260s 11805
50 100 200 0.2428s 13452
50 200 50 0.1174s 10553
50 200 100 0.1922s 10948
50 200 200 0.4359s 10751
在此种情况下我们仍然测得程序的运行时间和最短距离，发现遗传算法可以仍然可以在很短的时间内求解出结果，并且求解的全部结果与当前得到的最优解相比差别不大。总体来说遗传算法可以在较快速的情况下帮助我们求解出一个比较好的结果。

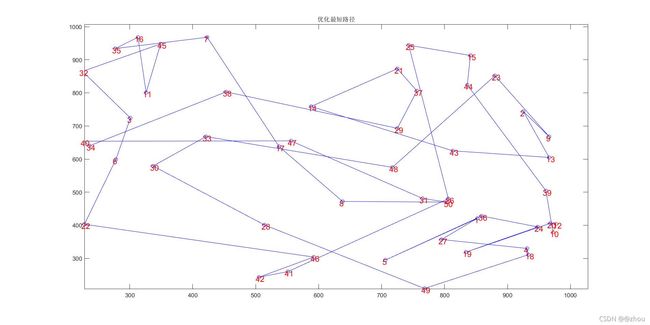
4. 与一般的暴力有限搜索方法对比。首先设置了最大的搜索次数为10000000次，我们可以得到下列的表格。

城市个数 计算方法 运行时间 最短距离
25 遗传算法 0.1473s 5055
25 穷举 3.5155s 5524
50 遗传算法 0.1174s 10553
50 穷举 29.3659s 19663

由此对比表格易得遗传算法的解决问题效率和解决问题的正确性都要比我们穷举法要好的多，尤其是在城市个数N较大的时候，我们发现遗传算法的效果更为明显。

代码附录

clear all;
close all;
clc;
N = 50;  %城市的个数
C = randi([200,1000],N,2);
%将对角线设置为0，并作出一个对称矩阵
D = zeros(N,N);
for i = 1:N
   for j  = 1:N
       D(i,j) = ((C(i,1) - C(j,1))^2 + (C(i,2) - C(j,2))^2)^0.5;
   end
end

tic;
NP = 50; 
G = 200;
f = zeros(NP,N);
F = [];
for i = 1:NP
    f(i,:) = randperm(N);
end
R = f(1,:);
len = zeros (NP,1);
gen = 0;

while gen < G
    for i = 1:NP
        len(i,1) = D(f(i,N),f(i,1));
        for j = 1:N-1
            len(i,1) = len(i,1) + D(f(i,j),f(i,j+1));
        end
    end
    maxlen = max(len);
    minlen = min(len);
    averlen = mean(len);
    
    rr = find(len == minlen);
    R = f(rr(1,1),:);
    
    for i = 1:length(len)
        fitness(i,1) = (1-((len(i,1)-minlen)/(maxlen-minlen+0.001)));
    end
    
    nn = 0;
    for i = 1:NP
        if fitness(i,1) >= rand
            nn = nn +1;
            F(nn,:) = f(i,:);
        end
    end
    
    [aa,bb] = size(F);
    
    while aa < NP
        nnper = randperm(nn);
        A = F(nnper(1),:);
        B = F(nnper(2),:);
        
        W = ceil(N/10);
        p = unidrnd(N-W+1);
        for i = 1:W
            x = find(A == B(p+i-1));
            y = find(B == A(p+i-1));
            temp = A(p+i-1);
            A(p+i-1) = B(p+i-1);
            B(p+i-1) = temp;
            temp =A(x);
            A(x) = B(y);
            B(y) = temp;
        end
        
        p1 = floor(1+N*rand());
        p2 = floor(1+N*rand());
        while p1 == p2
            p1 = floor(1+N*rand());
            p2 = floor(1+N*rand());
        end
        tmp = A(p1);
        A(p1) = A(p2);
        A(p2) = tmp;
        tmp  = B(p1);
        B(p1) = B(p2);
        B(p2) = tmp;
        F = [F;A;B];
        [aa,bb] = size(F);
    end
    if aa >NP
        F = F(1:NP,:);
    end
    f = F;
    f(1,:) = R;
    clear F;
    gen = gen +1;
    Rlength(gen) = minlen;
    averlength(gen) = averlen;
end
toc;
disp(min(averlength))
disp(num2str(toc))



figure
for i = 1:N-1
    plot([C(R(i),1),C(R(i+1),1)],[C(R(i),2),C(R(i+1),2)],'bo-');
    text(C(i,1)-5,C(i,2)-5,num2str(i),'Color','red','FontSize',14);
    hold on;
end
 plot([C(R(N),1),C(R(1),1)],[C(R(N),2),C(R(1),2)],'ro-');
 text(C(N,1)-5,C(N,2)-5,num2str(N),'Color','red','FontSize',14);
 title('优化最短路径');
 figure
 plot(Rlength,'r--');
 hold on;
 plot(averlength,'b-');
 legend('最优距离','平均距离');
 title('适应度进化曲线');
 
 
 tic;
 len = +inf;
 count  = 0;
 while len > 6000 && count < 10000000
     len = 0;
     f = randperm(N);
     len = D(f(1,N),f(1,1));
         for j = 1:N-1
             len = len + D(f(1,j),f(1,j+1));
         end
     count = count + 1;
 end
toc;
disp(num2str(toc))