[课程笔记]（图像分割入门到实战）

---

语义分割与实例分割概述

物体检测回归框的坐标点，分割是逐个像素做分类

语义分割的应用

目标检测太糙了，如果想知道精细的，每个像素属于哪一类

实例分割会将每个实例识别出来，可以理解为真正的目标检测的进化版本

语义分割数据集

在之前的alexnet和googlenet中我们通过缩放图像来将输入形状相同，但是对于语义分割工作而言并不合适，因为这样会破坏我们的标签映射。为了解决这个问题，我们通常将图片裁减为固定尺寸的小图。

一种是做模拟数据正广，另外就是采集这种图片

损失函数

1. cross entropy loss

用于图像语义分割任务的最常用损失函数是像素级别的交叉熵损失，这种损失会逐个检查每个像素，将对每个像素类别的预测结果（概率分布向量）与我们的独热编码标签向量进行比较。

假设我们需要对每个像素的预测类别有5个，则预测的概率分布向量长度为5：


补充：
二分类与多分类的交叉熵损失函数

2. weighted loss

由于交叉熵损失会分别评估 每个像素的类别预测，然后对所有像素的损失进行平均，因此我们实质上是在对图像中的每个像素进行平等地学习。如果多个类在图像中的分布不均衡，那么这可能导致训练过程由像素数量多的类所主导，即模型会主要学习数量多的类别样本的特征，并且学习出来的模型会更偏向将像素预测为该类别。

FCN论文和U-Net论文中针对这个问题，对输出概率分布向量中的每个值进行加权，即希望模型更加关注数量较少的样本，以缓解图像中存在的类别不均衡问题。

比如对于二分类，正负样本比例为1: 99，此时模型将所有样本都预测为负样本，那么准确率仍有99%这么高，但其实该模型没有任何使用价值。

为了平衡这个差距，就对正样本和负样本的损失赋予不同的权重，带权重的二分类损失函数公式如下：

3. Focal loss

上面针对不同类别的像素数量不均衡提出了改进方法，但有时还需要将像素分为难学习和容易学习这两种样本。

容易学习的样本模型可以很轻松地将其预测正确，模型只要将大量容易学习的样本分类正确，loss就可以减小很多，从而导致模型不怎么顾及难学习的样本，所以我们要想办法让模型更加关注难学习的样本。

对于较难学习的样本，将 bce loss 修改为：

4. Dice Loss

语义分割任务中常用的还有一个基于 Dice 系数的损失函数，该系数实质上是两个样本之间重叠的度量。此度量范围为 0~1，其中 Dice 系数为1表示完全重叠。Dice 系数最初是用于二进制数据的，可以计算为：

Dice loss是针对前景比例太小的问题提出的，dice系数源于二分类，本质上是衡量两个样本的重叠部分。

对于神经网络的输出，分子与我们的预测和标签之间的共同激活有关，而分母分别与每个掩码中的激活数量有关，这具有根据标签掩码的尺寸对损失进行归一化的效果。

对于每个类别的mask，都计算一个 Dice 损失：

将每个类的 Dice 损失求和取平均，得到最后的 Dice soft loss。

需要注意的是Dice Loss存在两个问题：

(1) 训练误差曲线非常混乱，很难看出关于收敛的信息。尽管可以检查在验证集上的误差来避开此问题。

(2) Dice Loss比较适用于样本极度不均的情况，一般的情况下，使用 Dice Loss 会对反向传播造成不利的影响，容易使训练变得不稳定。

所以在一般情况下，还是使用交叉熵损失函数。

总结：

1. 交叉熵损失把每个像素都当作一个独立样本进行预测，而 dice loss 和 iou loss 则以一种更“整体”的方式来看待最终的预测输出。

2. 这两类损失是针对不同情况，各有优点和缺点，在实际应用中，可以同时使用这两类损失来进行互补。

FCN全连接卷积神经网络

1. 对于一般的分类CNN网络，如VGG和Resnet，都会在网络的最后加入一些全连接层，经过softmax后就可以获得类别概率信息。但是这个概率信息是1维的，即只能标识整个图片的类别，不能标识每个像素点的类别，所以这种全连接方法不适用于图像分割。而FCN提出可以把后面几个全连接都换成卷积，这样就可以获得一张2维的feature map，后接softmax获得每个像素点的分类信息，从而解决了分割问题。
2. FCN是深度神经网络来做语义分割的奠定性工作，现在用的不多了

网络特点
3. 全卷积（Convolutional）
4. 上采样（Upsample）：转置卷积/反卷积
5. 跳跃结构（Skip Layer）

全卷积：

FCN将传统CNN中的全连接层转化成一个个的卷积层。如下图所示，在传统的CNN结构中，前5层是卷积层，第6层和第7层分别是一个长度为4096的一维向量，第8层是长度为1000的一维向量，分别对应1000个类别的概率。FCN将这3层表示为卷积层，卷积核的大小(通道数，宽，高)分别为（4096,1,1）、（4096,1,1）、（1000,1,1）。所有的层都是卷积层，故称为全卷积网络。

上采样——转置卷积：

可以发现，经过多次卷积（还有pooling）以后，得到的图像越来越小,分辨率越来越低（粗略的图像），那么FCN是如何得到图像中每一个像素的类别的呢？为了从这个分辨率低的粗略图像恢复到原图的分辨率，FCN使用了上采样。例如经过5次卷积(和pooling)以后，图像的分辨率依次缩小了2，4，8，16，32倍。对于最后一层的输出图像，需要进行32倍的上采样，以得到原图一样的大小。这个上采样是通过反卷积（deconvolution）实现的。

另外补充一句，上采样（upsampling）一般包括2种方式：

1. Resize，如双线性插值直接缩放，类似于图像缩放（这种方法在原文中提到）
2. Deconvolution，也叫Transposed Convolution

一张更为形象的说明如下：

跳跃结构：

对第5层的输出（32倍放大）反卷积到原图大小，得到的结果还是不够精确，一些细节无法恢复。于是Jonathan将第4层的输出和第3层的输出也依次反卷积，分别需要16倍和8倍上采样，结果就精细一些了。

其卷积过程类似：

1. image经过多个conv和+一个max pooling变为pool1 feature，宽高变为1/2
2. pool1 feature再经过多个conv+一个max pooling变为pool2 feature，宽高变为1/4
3. pool2 feature再经过多个conv+一个max pooling变为pool3 feature，宽高变为1/8
4. …
5. 直到pool5 feature，宽高变为1/32。

相对应的：

1. 对于FCN-32s，直接对pool5 feature进行32倍上采样获得32x upsampled feature，再对32x upsampled feature每个点做softmax prediction获得32x upsampled feature prediction（即分割图）。
2. 对于FCN-16s，首先对pool5 feature进行2倍上采样获得2x upsampled feature，再把pool4 feature和2x upsampled feature逐点相加，然后对相加的feature进行16倍上采样，并softmax prediction，获得16x upsampled feature prediction。
3. 对于FCN-8s，首先进行pool4+2x upsampled feature逐点相加，然后又进行pool3+2x upsampled逐点相加，即进行更多次特征融合。具体过程与16s类似，不再赘述。
   下图是这个卷积和反卷积上采样的过程：
   
   下图是32倍，16倍和8倍上采样得到的结果的对比，可以看到它们得到的结果越来越精确：
   
   优点（贡献）和不足
   优点和贡献

1.为深度学习解决语义分割提供了基本思路，激发了很多优秀的工作

2.输入图像大小没有限制，结构灵活

3.更加高效，节省时间和空间

不足

1.结果不够精细，边界不清晰

2.没有充分考虑到语义间的上下文关系

3.padding操作可能会引入噪声

网络结构：

Fully Convolutional Networks
他对每个像素的类别预测存储在通道k里面

转置卷积

参考链接

1. 上采样方法有很多，详见《【图像处理】详解 最近邻插值、线性插值、双线性插值、双三次插值_闻韶-CSDN博客》。然而，这些上采样方法都是基于人们的先验经验来设计的，在很多场景中效果并不理想 (如 规则固定、不可学习)。因此，我们希望神经网络自己学习如何更好地插值，即接下来要介绍的 转置卷积。
2. 曾经，转置卷积也被称为 反卷积 (Deconvolution)。与传统的上采样方法相比，转置卷积的上采样方式并非预设的插值方法，而是同标准卷积一样，具有可学习的参数，可通过网络学习来获取最优的上采样方式。
3. 转置卷积在某些特定领域具有广泛应用，比如：

3.1 在 DCGAN[1]，生成器将随机值转变为一个全尺寸图片，此时需用到转置卷积。
3.2 在语义分割中，会在编码器中用卷积层提取特征，然后在解码器中恢复原先尺寸，从而对原图中的每个像素分类。该过程同样需用转置卷积。经典方法有 FCN[2] 和 U-net[3]。
3.3 CNN 可视化[4]：通过转置卷积将 CNN 的特征图还原到像素空间，以观察特定特征图对哪些模式的图像敏感。

转置卷积和卷积的区别：

1. 卷积不会增大输入的高宽，通常要么不变、要么减半
2. 转置卷积则可以用来增大输入高宽

转置卷积的具体实现：

如图所示，input里的每个元素和kernel相乘，最后把对应位置相加，相当于卷积的逆变换

4. padding很难有效的吧你的高宽增加
5. 比如0会乘以核的每个元素，然后每个元素写在对应的地方

X和y的形状被交换了

其实就是padding在输出后把输出的矩阵的前padding行和列与后padding行和列给删除了而已。

实现二维转置卷积

import torch 
from torch import nn 
from d2l import torch as d2l 

def trans_conv(X, K):
    h, w = K.shape
    Y = torch.zeros((X.shape[0] + h - 1, X.shape[1] + w - 1))
    for i in range(X.shape[0]):
        for j in range(X.shape[1]):
            Y[i:i + h, j:j + w] += X[i, j] * K
    return Y

## 验证转置卷积
X = torch.tensor([[0.0, 1.0], [2.0, 3.0]])
K = torch.tensor([[0.0, 1.0], [2.0, 3.0]])
Y = trans_conv(X, K)
X,K,Y

(tensor([[0., 1.],
         [2., 3.]]),
 tensor([[0., 1.],
         [2., 3.]]),
 tensor([[ 0.,  0.,  1.],
         [ 0.,  4.,  6.],
         [ 4., 12.,  9.]]))

## 当输入x和卷积核k都是四维张量的时候，可以使用高级AIP获取到相同的结果
X, K = X.reshape(1, 1, 2, 2), K.reshape(1, 1, 2, 2) #(批量大小，通道数，高，宽)
tconv = nn.ConvTranspose2d(1, 1, kernel_size=2, bias=False)
tconv.weight.data = K
tconv(X)

tensor([[[[ 0.,  0.,  1.],
          [ 0.,  4.,  6.],
          [ 4., 12.,  9.]]]], grad_fn=<SlowConvTranspose2DBackward>)

填充
在转置卷积之中，填充是对输出进行填充，将输出外部n层褪去，所以加上填充是会缩小输出大小的

## 填充为1
tconv = nn.ConvTranspose2d(1, 1, kernel_size=2, padding=1, bias=False)
tconv.weight.data = K
tconv(X)

tensor([[[[4.]]]], grad_fn=<SlowConvTranspose2DBackward>)

转置卷积是一种卷积

等价于：


步幅在卷积里面使得高款成倍的减少，这里使得高宽成倍的增加

使用FCN进行语义分割

%matplotlib inline
import torch 
import torchvision
from torch import nn 
from torch.nn import functional as F 
from d2l import torch as d2l 
import os

模型构建

# 使用在ImageNet数据集上预训练的ResNet-18进行图像特征的提取，并将网络实例记为pretrained_net
# 注意ResNet-18的最后几层是全局平均池化层和全连接层，在FCN中不需要
pretrained_net = torchvision.models.resnet18(pretrained=True)
list(pretrained_net.children())[-3:]

[Sequential(
   (0): BasicBlock(
     (conv1): Conv2d(256, 512, kernel_size=(3, 3), stride=(2, 2), padding=(1, 1), bias=False)
     (bn1): BatchNorm2d(512, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
     (relu): ReLU(inplace=True)
     (conv2): Conv2d(512, 512, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
     (bn2): BatchNorm2d(512, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
     (downsample): Sequential(
       (0): Conv2d(256, 512, kernel_size=(1, 1), stride=(2, 2), bias=False)
       (1): BatchNorm2d(512, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
     )
   )
   (1): BasicBlock(
     (conv1): Conv2d(512, 512, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
     (bn1): BatchNorm2d(512, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
     (relu): ReLU(inplace=True)
     (conv2): Conv2d(512, 512, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
     (bn2): BatchNorm2d(512, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
   )
 ),
 AdaptiveAvgPool2d(output_size=(1, 1)),
 Linear(in_features=512, out_features=1000, bias=True)]

# 根据pretrained net创建一个新的网络实例，去除FCN不需要的部分
net = nn.Sequential(*list(pretrained_net.children())[:-2])

# 给定高宽为(320*480)的输入，net的前向网络将输入的高宽缩小到原来的1/32,即(10，15)
X = torch.rand(size=(1,3,320,480))
net(X).shape

torch.Size([1, 512, 10, 15])

# 使用1*1的卷积层将输出通道数转换为Pascal VO2012数据集的类别数（21类）.
# 这里的输出通道数选择21的原因是为了减少后面transpose层的计算量(减少到最小)
num_classes =21
net.add_module('final_conv',nn.Conv2d(512,num_classes,kernel_size=1))

net.add_module('transpose_conv',nn.ConvTranspose2d(num_classes,num_classes,kernel_size=64,padding=16,stride=32))

初始化转置卷积层

def bilinear_kernel(in_channels, out_channels, kernel_size):
    factor = (kernel_size + 1) // 2
    if kernel_size % 2 == 1:
        center = factor - 1
    else:
        center = factor - 0.5
    og = (torch.arange(kernel_size).reshape(-1, 1),
          torch.arange(kernel_size).reshape(1, -1))
    filt = (1 - torch.abs(og[0] - center) / factor) * \
           (1 - torch.abs(og[1] - center) / factor)
    weight = torch.zeros(
        (in_channels, out_channels, kernel_size, kernel_size))
    weight[range(in_channels), range(out_channels), :, :] = filt
    return weight

# 这里使用转置层实现双线性差值，构建一个输入高宽放大两倍的转置卷积层，并将卷积核使用`bilinear_kernel`函数构建
conv_trans = nn.ConvTranspose2d(3,3,kernel_size=4,padding=1,stride=2,bias=False)
conv_trans.weight.data.copy_(bilinear_kernel(3,3,4))

# 读取图像X，将上采样的结果记为Y,为了输出打印图片需要调整维度
img = torchvision.transforms.ToTensor()(d2l.Image.open('./course_file/pytorch/img/catdog.jpg'))
X = img.unsqueeze(0)
Y = conv_trans(X)
out_img = Y[0].permute(1, 2, 0).detach()
d2l.set_figsize()
print('input image shape:', img.permute(1, 2, 0).shape)
d2l.plt.imshow(img.permute(1, 2, 0))

input image shape: torch.Size([561, 728, 3])

print('output image shape:', out_img.shape)
d2l.plt.imshow(out_img);

可以看到，转置卷积层将图像的高和宽分别放大了2倍。除了坐标刻度不同，双线性插值放大的图像和原图看上去没什么两样。所以我们在全卷积网络中，[用双线性插值的上采样初始化转置卷积层。对于1 × 1 卷积层，我们使用Xavier初始化参数。]

W = bilinear_kernel(num_classes, num_classes, 64)
net.transpose_conv.weight.data.copy_(W);

损失函数

def loss(inputs, targets):
    return F.cross_entropy(inputs, targets, reduction='none').mean(1).mean(1)

num_epochs, lr, wd, devices = 5, 0.001, 1e-3, d2l.try_all_gpus()
trainer = torch.optim.SGD(net.parameters(), lr=lr, weight_decay=wd)

预测
预测时需要将输入图像在各个通道做标准化，并转换成卷积神经网络的四维输入格式

def predict(img):
    X = test_iter.dataset.normalize_image(img).unsqueeze(0)
    pred = net(X.to(devices[0])).argmax(dim=1)
    return pred.reshape(pred.shape[1],pred.shape[2])

Unet网络的编解码过程

U-Net与FCN都是很小的分割网络，既没有使用空洞卷积，也没有后接CRF，结构简单。
Unet的本质目标是解决小目标的分割问题，越深的网络感受野越大越更加适合大目标。所以Unet天生的优势是网络结构简单，适合做小目标

UNet结构包括编码器下采样、解码器上采样和同层跳跃连接三个组成部分。编码器由4组卷积、ReLU激活和最大池化构成，每一组均有两次33的卷积，每个卷积层后面都有一次ReLU激活函数，然后再进行一次步长为2的22最大池化进行下采样。

编码器下采样用于特征提取和语义信息浓缩，解码器上采样用于图像像素恢复，跳跃连接则用于信息补充。

网络结构

解码：线性插值

特征融合：相加或者拼接后过1*1卷积下采样

这个结构就是先对图片进行卷积和池化，在Unet论文中是池化4次，比方说一开始的图片是224x224的，那么就会变成112x112，56x56,28x28,14x14四个不同尺寸的特征。然后我们对14x14的特征图做上采样或者反卷积，得到28x28的特征图，这个28x28的特征图与之前的28x28的特征图进行通道伤的拼接concat，然后再对拼接之后的特征图做卷积和上采样，得到56x56的特征图，再与之前的56x56的特征拼接，卷积，再上采样，经过四次上采样可以得到一个与输入图像尺寸相同的224x224的预测结果。

Unet的好处我感觉是：网络层越深得到的特征图，有着更大的视野域，浅层卷积关注纹理特征，深层网络关注本质的那种特征，所以深层浅层特征都是有格子的意义的；另外一点是通过反卷积得到的更大的尺寸的特征图的边缘，是缺少信息的，毕竟每一次下采样提炼特征的同时，也必然会损失一些边缘特征，而失去的特征并不能从上采样中找回，因此通过特征的拼接，来实现边缘特征的一个找回。

为什么适用于医学图像？

（1）因为医学图像边界模糊、梯度复杂，需要较多的高分辨率信息。高分辨率用于精准分割。
（2）人体内部结构相对固定，分割目标在人体图像中的分布很具有规律，语义简单明确，低分辨率信息能够提供这一信息，用于目标物体的识别。UNet结合了低分辨率信息（提供物体类别识别依据）和高分辨率信息（提供精准分割定位依据），完美适用于医学图像分割。
（3）**可解释性重要。**由于医疗影像最终是辅助医生的临床诊断，所以网络告诉医生一个3D的CT有没有病是远远不够的，医生还要进一步的想知道，病灶在哪一层，在哪一层的哪个位置，分割出来了吗，能求体积嘛？同时对于网络给出的分类和分割等结果，医生还想知道为什么，所以一些神经网络可解释性的trick就有用处了，比较常用的就是画activation map。看网络的哪些区域被激活了，如下图。
（4）数据量少。医学影像的数据获取相对难一些，很多比赛只提供不到100例数据。所以我们设计的模型不宜多大，参数过多，很容易导致过拟合。 原始UNet的参数量在28M左右(上采样带转置卷积的UNet参数量在31M左右)，而如果把channel数成倍缩小，模型可以更小。缩小两倍后，UNet参数量在7.75M。缩小四倍，可以把模型参数量缩小至2M以内，非常轻量。个人尝试过使用Deeplab v3+和DRN等自然图像语义分割的SOTA网络在自己的项目上，发现效果和UNet差不多，但是参数量会大很多。

Unet++

设计更好的UNet结构和提升医学图像分割的精度，相关研究者提出了一种嵌套的UNet结构（Nested UNet），也叫UNet++，提出UNet++的论文为UNet++: A Nested U-Net Architecture for Medical Image Segmentation，发表于2018年的医学图像计算和计算机辅助干预（Medical Image Computing and Computer Assisted Intervention，MICCAI）会议上。

UNet++取名为嵌套的UNet，就在于其整体编解码网络结构中还嵌套了编解码的子网络（sub-networks），在此基础上重新设计UNet中间的跳跃连接，并补充了深监督机制加速网络训练收敛。完整的UNet++结构如下图所示。

图中黑色部分为原始的UNet结构，包括编码器下采样、解码器上采样和黑色虚线的跳跃连接三个部分；绿色部分即嵌套的UNet子网络，包括卷积和上采样两部分，而蓝色虚线部分就是UNet++重新设计后的跳跃连接，这部分跟DenseNet的密集连接类似，这里是为子网络提供跳跃连接；最上面红黑连线则是UNet++补充的深监督机制，目的是为了网络能够顺利得到训练。

下面我们从结构设计的角度来对UNet++进行解读。关于UNet结构，最首要的问题就是网络应该有几层，原始的UNet结构用了4层下采样和4层上采样，那么是不是4层就足以满足所有的分割任务需要？答案是否定的。通过本节之前的网络结构分析，我们已经知道，浅层网络能够提取图像粗粒度特征，获取图像基本形态；深层网络能够提取图像的抽象特征，获取图像语义信息，总之浅有浅的侧重，深有深的好处。同之前RefineNet的观点一样，UNet++的作者认为，不管是浅层、深层还是中层，所有层次的特征对于最后的分割都是重要的。有的数据分割任务简单，图像信息单一，可能浅层网络就足以达到很好的效果，而有的数据任务复杂，图像信息丰富，可能需要更深层的网络结构才能达到不错的效果，之前的UNet结构设计很难同时照顾到这种普适性。而UNet++通过设计不同深度的嵌套UNet子网络来实现这种普适性，所以UNet的深度到这里就解决了。

第二个问题则是加入不同深度的嵌套网络后，跳跃连接部分该如何调整。在UNet中，跳跃连接由同层编码器直连到编码器上采样对应层。但加入嵌套子网络后，UNet中原先的长连接就不复存在了，取而代之的是各子网络中的短连接。UNet++的作者们认为，长连接在UNet中是有必要的，能够将图像中前后信息联系起来，对于下采样造成的信息损失有很好的补充作用。所以，UNet++又参考DenseNet的密集连接设计，给嵌套网络补充了长连接，如下图5所示。

但是这样又带来了第三个问题：反向传播的时候中间部分可能会收不到由损失函数反传回来的梯度。所以见招拆招，UNet++又通过深监督的方法来强行加梯度，帮助网络正常进行训练。但深监督对于UNet++的好处绝不仅仅限于此，通过不同深监督损失函数，UNet++可以通过网络剪枝来实现可伸缩性。所以，总结来说UNet++相较于原始的UNet，有如下两个优势：

（1）通过嵌套子网络和长短连接来整合不同层次的图像特征，使得网络分割精度更高；

（2）灵活的网络结构配合深监督机制，让参数量巨大的深度网络在可接受的精度范围内能够大幅度的缩减参数量。

UNet++与UNet等网络分割效果对比如下图所示。

deeplab分割算法概述

简述空洞卷积的设计思路

DeepLab V1 为了避免池化引起的信息丢失问题，提出了空洞卷积的方式，这样可以在增大感受野的同时不增加参数数量，同时保证信息不丢失。为了进一步优化分割精度，还使用了 CRF（条件随机场）。

之前的语义分割网络的分割结果往往比较粗糙，原因主要是因为池化导致丢失信息，以及没有利用标签之间的概率关系。因此，作者针对性地提出，先使用空洞卷积来避免池化带来的信息损失，然后使用 CRF（条件随机场）进一步优化分割精度。
   空洞卷积的主要作用是在增大感受野的同时，不增加参数数量。VGG 中提出使用多个小卷积核代替大卷积核，该方法只能使感受野线性增长，而多个空洞卷积串联，可以实现指数增长。
   CRF 简单来说就是将每个像素点作为节点，像素与像素间的关系作为边，构成一个条件随机场。通过二元势函数描述像素点与像素点之间的关系，鼓励相似像素分配相同的标签，而相差较大的像素分配不同标签，而这个 “距离” 的定义与颜色值和实际相对距离有关。所以这样 CRF 能够使图片在分割的边界出取得比较好的效果。

DeepLab V2 在之前的基础上，增加了多尺度并行，解决了对不同大小物体的同时分割问题。

1. 用多尺度获得更好的分割效果（ASPP）；
2. 基础层由 VGG16 改为 ResNet；

其中，ASPP 的引入是最大也是最重要的改变。多尺度主要是为了解决目标在图像中表现为不同大小时仍能够有很好的分割结果（比如同样的物体，在近处拍摄时物体显得大，远处拍摄时显得小）。具体做法是并行的采用多个采样率的空洞卷积提取特征，再将特征融合，类似于空间金字塔结构，形象的称为 Atrous Spatial Pyramid Pooling （ASPP）。具体形式如下图

DeepLab V3 将空洞卷积应用在了级联模块，并且改进了 ASPP 模块。

1. ASPP 中应用了 BN 层
2. 使用模型最后的特征映射的全局平均池化（为了克服远距离下有效权重减少的问题）；
   

DeepLab V3+ 使用空间金字塔池化模块（SPP）和编码解码结构，是用于语义分割的深度网络结构。

1.目标大，2. 识别难

感受野：33->55

假设：1. 相邻像素相似2.空洞卷积可以防止过拟合

条件随机场CRF和隐马尔科夫随机场HMM

概率模型与条件随机场

概率模型与条件随机场
机器学习中的很多模型可以根据概率分布形式分为生成模型和判别模型，其中生成模型以输入输出的联合分布P(X,Y)为基础建模，如朴素贝叶斯、隐马尔可夫模型；判别模型以条件概率分布P(Y|X)为基础建模，如最大熵模型、条件随机场等。这几个模型之间有一定的关系，它们的关系如下：

其中，NB表示朴素贝叶斯，ME表示最大熵，HMM表示隐马尔科夫，CRF表示条件随机场。joint联合分布，conditional条件分布。single class输出单一类别，sequence输出序列。例如，朴素贝叶斯将输出y扩展成序列，就可以以此为基础构造HMM；在满足输入条件下的HMM可以扩展成CRF。
从朴素贝叶斯, 到HMM有如下转换关系:

这里面，朴素贝叶斯假设最强 ，因为它要求所有输入特征之间条件独立；这是一种为计算方便而做的近似假设，然而现实中基本不会有模型符合输入特征间的独立，因此以朴素贝叶斯建模一般会有精度损失。

隐马尔科夫模型进了一步，它考虑一定的变量相关性，如马尔科夫假设状态序列中，当前状态只与其前一个状态有关，如：

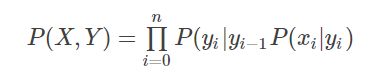
但是HMM只考虑了状态之间的邻接关系，没有考虑观测序列间的关系，条件随机场刚好弥补了这个缺陷。所以条件随机场是一个相对比较完善的模型，但代价是计算复杂性的提高。

补充理解
朴素贝叶斯(NB)、逻辑回归(LR)、隐马尔科夫模型(HMM)、条件随机场(CRF)

1. 朴素贝叶斯：生成式模型，条件独立 —> 序列形式 隐马尔科夫模型 —> 图形式 通用有向图模型
2. 逻辑回归：判别式模型，条件不独立 —> 序列形式 线性链条件随机场 —> 序列形式 通用条件随机场

朴素贝叶斯(NB)
条件独立性假设: 特征之间互相独立，没有耦合，互不干扰。

逻辑回归(LR)

注意逻辑回归和线性回归都是回归，但是线性回归就是用来回归，而是逻辑回归回归的是概率，是用来分类的，这是因为由于条件之间不独立，不能求出联合概率分布，只能回归后验概率，大于0.5即为yes，所以是判别模型

隐马尔科夫模型(HMM)

HMM模型中存在两个假设：一是输出观察值之间严格独立，二是状态的转移过程中当前状态只与前一状态有关。

条件随机场(CRF)

因为HMM只限定在了观测与状态之间的依赖，而MEMM引入自定义特征函数，不仅可以表达观测之间的依赖，还可表示当前观测与前后多个状态之间的复杂依赖。

这里由于去掉了独立性假设，所以不能给出联合概率分布，只能求后验概率，所以是判别模型

条件随机场CRF

概率图模型可大致分为两类：一类是有向图模型，表示变量间的依赖关系，也称为贝叶斯网；一类是无向图模型，表示变量间的相关关系，也称为马尔科夫网或马尔科夫随机场。

条件随机场这个概念比较大，一般在做序列标注的时候，我们用的是所谓的线性链条件随机场，加了线性两个字，说明结点之间的依赖关系是线性的。

广义的条件随机场可以是一个任意的概率图模型，比如下面这种：

其中每个结点表示一个随机变量，变量之间的连边表示变量之间有依赖关系。

这里问一个问题：A, B, C, D, E 最可能的取值是什么？

我们当然知道是令联合分布 P(A, B, C, D, E) 最大的取值。但是这个分布似乎过于复杂。它可以拆解吗？

答案是可以的。这里有一个定理：无向概率图的概率等于其中每个极大团的概率的乘积。

这里的团（clique）意思是互相之间都有连边的点的集合。比如说 B，C，D 两两之间都有连边，所以它们三个组成一个团。同理，A，B 和 D，E 分别也是两个团。而极大团的意思是说这个团已经尽可能大了，比如说 B，C 虽然构成一个团，但它不是最大团，因为 B，C，D 这个团更大，而且包含了 B，C 这个团。而 A，B 和 D，E 还是极大团，因为没有包含它们的更大的团了。所以，上面这个联合分布 P(A, B, C, D, E) 可以拆解成 P(A, B) * P(B, C, D) * P(D, E)，这样计算就容易多了。

说完广义的条件随机场，下面开始讲线性链条件随机场。

一般来说，用于序列标注的线性链条件随机场，是一个这样的概率图模型：

这里面有六个变量：三个单词，以及它们各自的词性标注。其中相邻的词语有依赖关系，词语和词性有依赖关系，但是词性之间没有依赖关系。

这里我们可以对比一下 HMM 的建模。用于序列标注的 HMM，典型的建模是这样的：

这里面可以发现线性链条件随机场和 HMM 的明显区别：

HMM 是有向图模型，词语分先来后到。前面的词语决定了（生成了）后面的词语，因此我们可以使用类似 P(love|Verb) 这样的条件分布来建模一个动词是 love 的概率。而在线性链条件随机场当中，变量之间没有先后，是共同产生的关系，因此我们需要类似 P(love, Verb) 这样的联合分布来建模一个位置是 love 这个动词的概率。

全连接CRFs后处理

参考

1. 目前图像像素级语义分割比较流行使用深度学习全卷积神经网络FCN或者各种FCN的改进版U-Net、V-Net、SegNet等方法。这些模型中使用了反卷积层进行上采样操作，虽然能够将特征图恢复至原图尺寸，但也造成了特征的损失，自然而然产生了分类目标边界模糊的问题。
2. 为了得到更精确的最终分类结果，通常要进行一些图像后处理。全连接CRFs是在目前深度学习图像分割应用中常用的一种图像后处理方式，它是CRFs的改进模式，能够结合原始影像中所有像素之间的关系对深度学习得到的分类结果进行处理，优化分类图像中粗糙和不确定性的标记，修正细碎的错分区域，同时得到更细致的分割边界。

例如：

处理前的结果：

处理后的结果：
仔细看变化还是挺大的，去掉了很多杂质，让类别分布更纯粹

全连接条件随机场使用二元势函数解释了一个像素与另一个像素之间的关系，给像素关系紧密的两个像素赋予相同的类别标签，而关系相差很大的两个像素会赋予不同的类别标签，这个“关系”的判断与像素的颜色值、像素间的相对距离都有关系。全连接条件随机场中二元势函数解释了每一个像素与其他所有像素的关系，与条件随机场相比，“全连接”更加紧密一些。

在全连接CRFs进行影像后处理的实际操作中，一元势能为概率分布图，即由模型输出的特征图经过softmax函数运算得到的结果；二元势能中的位置信息和颜色信息由原始影像提供。当能量E(x)越小时，预测的类别标签X就越准确，我们通过迭代最小化能量函数，得到最终的后处理结果。

@ray.remote
def custom_crf(mask_img, shape=(256, 256)):
    # Converting annotated image to RGB if it is Gray scale
    if(len(mask_img.shape)<3):
        mask_img = gray2rgb(mask_img)
        
    # Converting the annotations RGB color to single 32 bit integer
    annotated_label = mask_img[:,:,0] + (mask_img[:,:,1]<<8) + (mask_img[:,:,2]<<16)
    
    # Convert the 32bit integer color to 0,1, 2, ... labels.# 将uint32颜色转换为1,2,...
    colors, labels = np.unique(annotated_label, return_inverse=True)

    n_labels = 2
    
    # Setting up the CRF model
    d = dcrf.DenseCRF2D(shape[1], shape[0], n_labels)

    # Get unary potentials (neg log probability)# 得到一元势（负对数概率）一元势即网络预测得到的结果，进行-np.log(py)等操作
    U = unary_from_labels(labels, n_labels, gt_prob=0.7, zero_unsure=False)
    d.setUnaryEnergy(U)

    # This adds the color-independent term, features are the locations only.
     # 增加了与颜色无关的术语，只是位置-----会惩罚空间上孤立的小块分割,即强制执行空间上更一致的分割
     #二元势即用于描述像素点和像素点之间的关系，鼓励相似像素分配相同的标签，而相差较大的像素分配不同的标签。这个相似的定义与颜色值srgb和实际相对距离sxy相关，所以CRF能够使图片尽量在边界处分割。

#d.addPairwiseGaussian这个函数创建的是颜色无关特征，这里只有位置特征(只有参数实际相对距离sxy)，并添加到CRF中
    d.addPairwiseGaussian(sxy=(12, 12), compat=4, kernel=dcrf.DIAG_KERNEL,
                      normalization=dcrf.NORMALIZE_SYMMETRIC)
        
    # Run Inference for 20 steps 
    Q = d.inference(20)

    # Find out the most probable class for each pixel.
    # 找出每个像素最可能的类
    MAP = np.argmax(Q, axis=0)

    return MAP.reshape((shape[0], shape[1]))

参考