LeetCode题目——数组篇
文章目录
- 前言
- 一、LeetCode——二分查找
- 二、LeetCode——移除元素
-
- 1.暴力解法
- 2、双指针法
- 三、LeetCode——有序数组的平方
-
- 1、暴力解法
- 2、双指针法
- 四、LeetCode——长度最小子数组
-
- 1、暴力解法
- 2、滑动窗口(双指针法)
- 五、LeetCode——在排序数组中查找元素的第一个和最后一个位置
- 六、LeetCode——螺旋矩阵
前言
数组是存放在连续内存空间上的相同类型数据的集合。
需要两点注意的是:
1.数组下标都是从0开始的。
2.数组内存空间的地址是连续的。
正是因为数组的在内存空间的地址是连续的,所以我们在删除或者增添元素的时候,就难免要移动其他元素的地址。
一、LeetCode——二分查找

如果题目中给出了数组,并且有查找操作,优先考虑二分查找,二分查找法是速度比较快的查找方式,大多数情况使用二分查找基本上是在数组有序的前提下。但是也有在无序的情况下使用。
class Solution:
def search(self, nums: List[int], target: int) -> int:
left,right = 0,len(nums)-1
while left<=right:
mid = left+(right-left)//2 #为了防止溢出,可以把这个当做求中间下标的固定写法
if nums[mid] == target: #如果中间的值等于目标值,返回mid
return mid
elif nums[mid] < target: #如果小于目标值,则在右半边继续递归的寻找
left = mid+1
else: #如果大于目标值,则在左半边继续递归的寻找
right = mid-1
return -1
该题目是比较简单的题目,可以当做数组的基础来看。二分查找也经常使用递归来完成,其大体思路和上述一样。
二、LeetCode——移除元素

在数组中可以说并没有明确的删去元素的操作,,如果要删除一个元素,只是把该元素覆盖掉,覆盖的方法就是将数组后的元素前移。
1.暴力解法
遍历数组,当遇到等于x的情况时,让该位置以后的元素依次向前移动一个位置。因为可能会出现需要删除的元素相邻的情况,所以i也要往前一位。
// 时间复杂度:O(n^2)
// 空间复杂度:O(1)
class Solution {
public:
int removeElement(vector<int>& nums, int val) {
int size = nums.size();
for (int i = 0; i < size; i++) {
if (nums[i] == val) { // 发现需要移除的元素,就将数组集体向前移动一位
for (int j = i + 1; j < size; j++) {
nums[j - 1] = nums[j];
}
i--; // 因为下标i以后的数值都向前移动了一位,所以i也向前移动一位
size--; // 此时数组的大小-1
}
}
return size;
}
};
2、双指针法
双指针是一种非常高效的思想,经常应用于数组和链表中。
在此题中,我们可以定义两个指针slow和fast,当当前元素不等于x时,这两个指针一起向后移,当等于x时,fast指针后移,slow指针不变。然后用fast指针指向的元素覆盖掉slow指针指向的元素。遍历结束后,数组的长度就是slow。
class Solution:
def removeElement(self, nums: List[int], val: int) -> int:
slow = fast = 0 #初始化都为0
while fast<len(nums):
if nums[fast]!=val: #当不等的时候,一起向后移;相等的时候,slow不变,fast后移
nums[slow]=nums[fast]
slow+=1
fast+=1
return slow #返回数组的长度
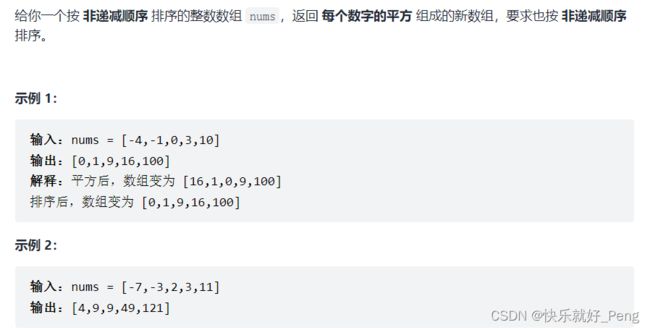
三、LeetCode——有序数组的平方
1、暴力解法
暴力解法很简单,不多做解释
class Solution:
def sortedSquares(self, nums: List[int]) -> List[int]:
for i in range(len(nums)):
nums[i] *= nums[i]
nums = sorted(nums)
return nums
2、双指针法
'''
采用双指针的方法,额外新建一个数组存放返回结果。
因为原数组也已经排好序了,所以平方后的数最大的要么是原数组中的第一个元素要么是最后一个元素。
将最大的放在res数组最后一个位置,依次遍历
'''
class Solution:
def sortedSquares(self, nums: List[int]) -> List[int]:
i,j,k = 0,len(nums)-1,len(nums)-1
res = [-1]*len(nums)
while i<=j:
lm = nums[i]*nums[i]
rm = nums[j]*nums[j]
if lm > rm:
res[k] = lm
i += 1
else:
res[k] = rm
j -= 1
k -= 1
return res
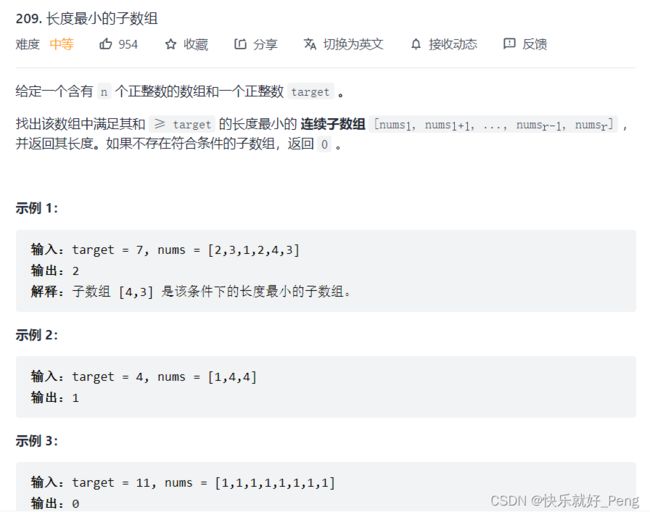
四、LeetCode——长度最小子数组
1、暴力解法
class Solution:
def minSubArrayLen(self, target: int, nums: List[int]) -> int:
res = float('inf') #res初始化为无穷大
sum,sublenth = 0,0 #sum为当前和,sublenth为符合条件的序列的长度
for i in range(0,len(nums)): #i为子序列的起点
sum = 0
for j in range(i,len(nums)): #j为子序列的终止位置
sum += nums[j]
if sum>=target: #如果符合要求,就算出当前序列的长度,并与res比较
sublenth = j-i+1
res = min(res,sublenth)
break #只要找到一个符合要求的,就break
return res if res != float('inf') else 0 #如果res没有被赋值,就返回0
2、滑动窗口(双指针法)
所谓滑动窗口,就是不断的调节子序列的起始位置和终止位置,从而得出我们要想的结果。
在本题中实现滑动窗口,主要确定如下三点:
- 窗口内是什么?
- 如何移动窗口的起始位置?
- 如何移动窗口的结束位置?
窗口就是 满足其和 ≥ s 的长度最小的 连续子数组。
窗口的起始位置如何移动:如果当前窗口的值大于s了,窗口就要向前移动了(也就是该缩小了)。
窗口的结束位置如何移动:窗口的结束位置就是遍历数组的指针,窗口的起始位置设置为数组的起始位置就可以了。
'''
滑动窗口
'''
class Solution:
def minSubArrayLen(self, target: int, nums: List[int]) -> int:
res = float('inf')
subLenth = 0
sum,index = 0,0 #sum为当前数组元素和,index为滑动窗口的起始位置
for i in range(len(nums)):#滑动窗口的终止位置为遍历数组的指针
sum += nums[i]
while sum>=target:
subLenth = i-index+1
res = min(subLenth,res)
sum -= nums[index] #不断地变更序列的起始位置
index += 1
return 0 if res==float("inf") else res
五、LeetCode——在排序数组中查找元素的第一个和最后一个位置
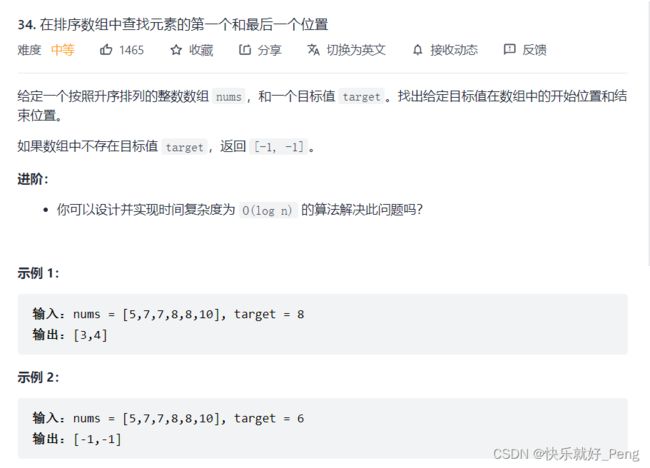
用两个二分查找,一个二分查找查找左边界,另一个查找右边界。
该题可以分为三个情况:
- target 在 nums[0] ~ nums[n-1] 中,nums 中存在 target。例如 nums = [5,7,7,8,8,10],target = 8,返回 [3,4]。
- target 在 nums[0] ~ nums[n-1] 中,nums 中不存在 target。例如 nums = [5,7,7,8,8,10],target = 6,返回 [-1,-1]。
- target < nums[0] 或者 target > nums[n-1]。例如 nums = [5,7,7,8,8,10], target = 4,返回 [-1,-1]。
查找左边界:
def searchLeft(nums,target): #寻找左边界
left,right = 0,len(nums)-1
while(left<=right):
mid = left+(right-left)//2
if nums[mid]<target:
left=mid+1
else:
right=mid-1
if nums[left]==target:
return left
else:
return -1
普通二分查找是,当 nums[mid] == target 时,直接返回 mid,而在本题中,则是要继续向左查找,看是否还有和 target 相等的数组元素。
查找右边界
def searchRight(nums,target): #寻找右边界
left,right = 0,len(nums)-1
while(left<=right):
mid = left+(right-left)//2
if nums[mid]>target:
right=mid-1
else:
left=mid+1
if nums[right]==target:
return right
else:
return -1
当nums[mid]=target时,一直向右找,看是否还有和 target 相等的数组元素。
不要忘记还有一种情况:
if len(nums)==0 or nums[0]>target or nums[-1]<target:
return [-1,-1]
完整代码:
class Solution:
def searchRange(self, nums: List[int], target: int) -> List[int]:
def searchLeft(nums,target): #寻找左边界
left,right = 0,len(nums)-1
while(left<=right):
mid = left+(right-left)//2
if nums[mid]<target:
left=mid+1
else:
right=mid-1
if nums[left]==target:
return left
else:
return -1
def searchRight(nums,target): #寻找右边界
left,right = 0,len(nums)-1
while(left<=right):
mid = left+(right-left)//2
if nums[mid]>target:
right=mid-1
else:
left=mid+1
if nums[right]==target:
return right
else:
return -1
if len(nums)==0 or nums[0]>target or nums[-1]<target:
return [-1,-1]
lb = searchLeft(nums,target)
rb = searchRight(nums,target)
return [lb,rb]
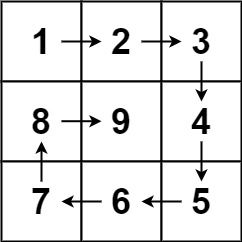
六、LeetCode——螺旋矩阵
class Solution:
def generateMatrix(self, n: int) -> List[List[int]]:
matrix = [[0] * n for _ in range(n)]
left,right,up,down = 0,n-1,0,n-1
number = 1
while left<right and up<down:
for x in range(left,right):
matrix[up][x] = number
number += 1
for y in range(up,down):
matrix[y][right] = number
number += 1
for x in range(right,left,-1):
matrix[down][x] = number
number += 1
for y in range(down,up,-1):
matrix[y][left] = number
number += 1
left += 1
right -= 1
up += 1
down -= 1
#奇数的话需要给中间的赋值
if n%2 != 0:
matrix[n//2][n//2] = number
return matrix