随机数字信号处理期末大报告——基于卡尔曼滤波的自由落体运动目标跟踪MATLAB实现
完整的实验报告下载随机数字信号处理期末大报告-基于卡尔曼滤波的自由落体运动目标跟踪.docx-机器学习文档类资源-CSDN下载
程序包及所需数据下载
target tracking using kalman.zip
一、实验题目
基于卡尔曼滤波的自由落体运动目标跟踪
二、实验原理
卡尔曼滤波是一种利用线性系统状态方程,通过系统输入输出观测数据,对系统状态进行最优估计的算法。由于在观测的过程中,常常伴有噪声和干扰,最优估计后会达到一个滤波的效果,所以,也可将其看作一个滤波过程。
卡尔曼滤波可以在任何含有不确定性信息的动态系统中,对系统的下一步走向做出有根据的预测。即使伴随着各种干扰,卡尔曼滤波总是能指出真实发生的情况。
卡尔曼滤波的一个典型实例是从一组有限的、对物体位置的、包含噪声的观察序列中预测出物体的坐标位置和速度。下面就以一个汽车在路面行驶为例,来说明卡尔曼滤波的基本原理。
2.1 状态转移
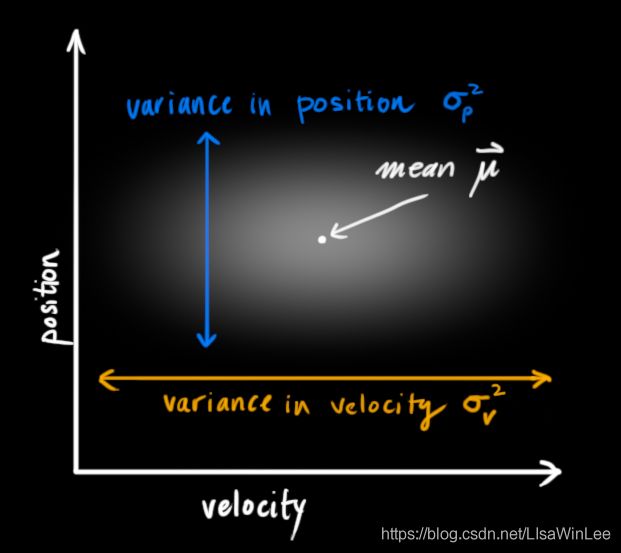
假设有一辆汽车在路面行驶,如图2.1所示。用位置和速度来表示他当前的状态,写成矩阵的形式就是xt=ptvt ,其中pt 代表当前时刻的位置,vt 代表当前时刻汽车的速度。卡尔曼滤波假设两个变量都是随机的,并且服从高斯分布。每个变量都有一个均值,表示随机分布的中心,以及方差,表示不确定性。
图2.1 一辆汽车在路面行驶示意图
若在实际情况下,司机常常会有踩油门和刹车的动作,在运动状态里相当于给汽车一个加速度ut 。此时,写出运动时的位移和速度公式,如公式(2-1)和(2-2)所示。
pt=pt-1+vt-1×∆t+ut×∆t22 (2-1)
vt=vt-1+ut×∆t (2-2)
通过观察这两个公式,输出变量是输入变量的线性组合,这就是称卡尔曼滤波是最佳的线性滤波器的原因,因为它描述两个状态间的线性关系。因为是线性关系,所以可以进一步将两个运动公式写成矩阵的形式,如公式(2-3)所示。
ptvt=1∆t01pt-1vt-1+∆t22∆tut (2-3)
若将其中的两个状态变化矩阵提取出来,则Ft=1∆t01 为状态转移矩阵,它表示如何从上一时刻状态推测当前时刻状态,Bt=∆t22∆t 为控制矩阵,它控制着加速度ut 对整个运动的作用。这样处理后,就可以将公式简化为
xt_=Ftxt-1+Btut (2-4)
公式(2-4)表示状态预测公式。
得到状态预测公式后,就可以推测当前时刻的状态,不过所有的推测都是包含噪声的,噪声越大,不确定性就越大,那么如何表示这次推测带来了多少不确定性,这时候就用协方差矩阵来表示。
2.2 协方差矩阵
(a) (b)
图2.2 位置和速度的关系图
在图2.2 (a)中,位置和速度是不相关的,这意味着由其中一个变量的状态无法推测出另一个变量可能的值。而图2.2(b)中,位置和速度是相关的,观测特定位置的可能性取决于当前的速度。这种情况是有可能发生的,例如,我们基于上一时刻的位置来估计当前时刻的位置。如果速度过高,我们可能已经移动很远了。如果缓慢移动,则距离不会很远。因此,跟踪这种关系是非常重要的,因为它可以包含更多的信息,其中一个测量值可以告知其它变量可能的值。这就是卡尔曼滤波的目的,尽可能地在包含不确定性的测量数据中提取更多信息。
这种相关性用协方差矩阵来表示,矩阵中的每个元素aij 表示第i 个和第j 个状态变量之间的相关度。协方差的一般表示形式为covx,x=σ11σ12σ12σ22 ,在这里用P 表示。
接下来,为了实现不确定性在每个时刻传递,需要让协方差矩阵P 乘以状态转移矩阵F ,根据协方差矩阵乘法的性质,可以得到公式
Pt-=FPt-1FT (2-5)
预测模型并不是百分百准确的,还包含噪声,因此还需要在公式后面加协方差矩阵Q,来表示预测模型本身带来的噪声。
Pt-=FPt-1FT+Q (2-6)
它表示不确定性在各个时刻之间的传递关系。
2.3 观察矩阵
假设路边有个激光测距仪,负责测量汽车在行驶过程中的位置变化,每一时刻都可以观测到汽车的位置,观测到的值记为zt 。
图2.3 激光测距仪时刻测量汽车位置示意图
那么从汽车本身的状态xt 到观测状态zt 之间有一个变化关系,记为H ,表示为H=10 。两者之间的关系可以用公式(2-7)表示,其中v 表示观测矩阵带来的噪声。另外,在观测过程中,ye存在噪声带来的不确定性,此时用R 来表示观测噪声的协方差矩阵。
zt=Hxt+v (2-7)
2.4 状态更新
预测状态值和观察值都已经准备好,接下来就是卡尔曼滤波算法的核心部分,用卡尔曼系数进行状态更新,公式如(2-8)所示。
xt=xt_+Kt(zt-Hxt_) (2-8)
通过拆分这个公式,来更好的理解它的意义。其中,zt-Hxt_ 表示实际观测值与预期观测值之间的残差,这个残差乘上系数Kt 就可以修正xt 的值。Kt 叫卡尔曼系数,实际上是个矩阵,它的表达式为
Kt=Pt-HT(HPt-HT+R)-1 (2-9)
作用有两个方面:一是权衡预测状态协方差P 和观察量的协方差矩阵R 的大小,来决定两者所占的权重,是相信预测模型多一点还是观测模型多一点。如果相信预测模型多一点,那么残差的权重就会小一点;如果相信观察模型多一点,那么残差的权重就会大一些。二是把残差的作用从观察域转换到状态域。因为,观察值zt 是一个一维向量,状态xt 是一个二维向量,他们所用的单位及特征都有可能是不同的,为了用状态值的残差去更新状态值,就需要用卡尔曼系数Kt 来做这个转换。
2.5 噪声协方差矩阵的更新
最后一步就是更新最佳估计值的噪声分布,
Pt=I-KtHPt- (2-10)
这个值是留给下一个迭代值用的,在这一步里,状态的不确定性是减小的,而在下一轮迭代中,由于传递噪声的引入,不确定性就会增大,卡尔曼滤波就是在这种不确定性中寻求一种平衡的。
2.6 小结
以上公式中,(2-4)和(2-6)表示通过上一时刻的状态来预测当前时刻的状态,而(2-8)、(2-9)和(2-10)指用当前的观测值来更新xt_ 和Pt- ,经过更新后的值就是最佳的观测值。
三、实验内容
实验一:给定参数表示自由落体运动,通过卡尔曼滤波算法对其进行目标跟踪,测量跟踪效果误差,用折线图表示出来,以供分析。
实验二:选用60幅图像,每幅图像均展示了小球在下降过程中的一个状态,按时间顺序排列,不断地更换图片即可以看到小球从下降到反弹直至动能为0的这样一个状态。连续的对60幅图像进行卡尔曼滤波,进行目标跟踪预测。
四、实验过程
4.1 实验平台
本次实验均在MATLAB数学软件内实现,其由一系列工具组成,是一个高级的矩阵语言,包含大量计算算法,具有方便的数据可视化功能,目前对许多专门的领域都开发了功能强大的模块集和工具箱。此次实验可以利用MATLAB编程,可以看到矩阵数据的变化,绘制出折线图,以及目标跟踪的效果动画。
4.2 模拟自由落体运动时卡尔曼滤波进行目标跟踪
自由落体运动的定义是物体初速度为0,只受重力的作用,做匀加速直线运动。那么,为了模拟自由落体运动,将过程噪声方差设置为0,即忽略空气阻力。加速度设置为1,仿真1000步长。设定各个参数如下:
状态转移矩阵:F=1∆t01 ,∆t=1 ;
控制矩阵:B= 0.51 ;
观测矩阵:H=10 ;
状态转移协方差矩阵:Q=0000 ;
观测噪声方差:R=1 ;
状态协方差矩阵:P=10001 。
将各个数据作为系统输入通过卡尔曼滤波,经过卡尔曼滤波的不断迭代更新,达到去除噪声实现目标跟踪的效果。通过计算测量误差和卡尔曼滤波的估计误差,比较两个误差的变化,得出卡尔曼滤波的作用。
4.2 利用卡尔曼滤波对运动小球做目标跟踪
通过上一个实验已经得到卡尔曼滤波可以用于自由落体运动的目标跟踪,但在现实生活中,运动是复杂多变的,这时卡尔曼滤波的目标跟踪效果更值得研究。为了体现小球做连续运动的效果,选取小球做下降、上弹运动的连续60张图像作为系统输入,如图4.1所示。
图4.1 小球运动图像(60张)
设定各个参数如下:
状态转移矩阵:F=1001∆t00∆t00001001 ,∆t=1 ;
观测矩阵:H=10010000 ;
状态转移协方差矩阵:=0.01000.010 00 00 00 00.01000.01 ;
观测噪声方差:R=0.28450.00450.00450.0455 ;
状态协方差矩阵:P=100001000 00 00 00 010000100 。
初始化好卡尔曼滤波后,陆续读取这60张小球运动的图像,通过卡尔曼滤波算法不断地对小球下一步运动进行预测和更新,达到目标跟踪的目的。
五、实验结果
5.1 模拟自由落体运动时卡尔曼滤波的结果
自由落体运动中,误差来自于观测时带来的误差和干扰,为了模拟这一效果,人为的随机加入一段观测噪声,并将其输出来,如图5.1所示。
图5.1 测量噪声折线图
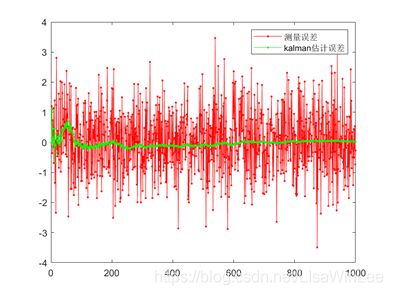
经过卡尔曼滤波后,误差逐渐减小,最后停留在0值附近。如图5.2所示为测量误差与卡尔曼滤波估计误差的对比图,红色折线为测量误差,绿色折线为卡尔曼滤波估计误差。
图5.2 测量误差与kalman估计误差对比图
接下来,从卡尔曼滤波的原理方面来测量此次实验的效果。卡尔曼滤波的作用原理就是通过调节卡尔曼系数,使误差均方值尽可能达到最小的过程。因此,将误差均方值的变化曲线绘制出来。
图5.3 位移与速度的误差均方值曲线
从图5.3可以看出,大约在50步长附近,就可以使误差均方值达到最小,卡尔曼滤波在自由落体运动中的效果显著。
5.2 小球运动时卡尔曼滤波的目标跟踪结果
通过连续的对60张小球运动图像进行卡尔曼滤波,用不同颜色的圆圈将小球的真实位置和卡尔曼滤波的估计位置标记出来,绿色圆圈代表小球的真实位置,红色代表估计位置,如图5.4所示的几幅图,为其中几部分结果展示。
(a) (b)
(c) (d)
图5.4 小球运动真实位置和kalman估计位置标识图
从图5.4 中可以看出,小球最开始运动时卡尔曼滤波的估计是相对准确的,如图(a)、(b)所示。但当小球出现反弹动作时,即运动方向发生了改变,卡尔曼滤波的预估效果受到了一些影响,如图(c)所示。不过经过几个步长后,卡尔曼滤波的估计位置又回到了正确的位置上,如图(d)所示。此实验虽有一定误差,但仍不失为卡尔曼滤波的目标跟踪。后续在参数的设定上再进一步做一些测试和改动,效果会更好。
六、总结与展望
通过课程学习和实验探索,我知道了卡尔曼滤波是利用线性系统状态方程,通过系统的输入输出观测数据,对系统状态进行最有估计的计算。实验一中,将卡尔曼滤波应用于自由落体运动的目标跟踪。测量观测误差和卡尔曼估计误差,通过比较,可以得到卡尔曼滤波的效果是很好的,能够在几十个步长内将误差减小到0左右,达到目标跟踪的效果。实验二中,将卡尔曼滤波应用到现实中的小球落地运动中。通过输出的结果可以看出,卡尔曼滤波在特定步长内是可以实现目标跟踪的。
实验二的效果还不是特别好,且本次实验的根本是基于图像滤波,分析情景相对简单。未来会改进算法的参数设置,并且尝试将卡尔曼滤波直接应用于视频内的物体运动跟踪。
七、附录
7.1 卡尔曼滤波应用于自由落体运动的目标跟踪
function freefall
N=1000; %仿真时间,时间序列总数
%噪声
Q=[0,0;0,0];%过程噪声方差为0,即下落过程忽略空气阻力
R=1; %观测噪声方差
W=sqrt(Q)*randn(2,N);%既然Q为0,即W=0
V=sqrt(R)*randn(1,N);%测量噪声V(k)
%系数矩阵
A=[1,1;0,1];%状态转移矩阵
B=[0.5;1];%控制量
U=-1;
H=[1,0];%观测矩阵
%初始化
X=zeros(2,N);%物体真实状态
X(:,1)=[95;1];%初始位移和速度
P0=[10,0;0,1];%初始误差
Z=zeros(1,N);
Z(1)=H*X(:,1);%初始观测值
Xkf=zeros(2,N);%卡尔曼估计状态初始化
Xkf(:,1)=X(:,1);
err_P=zeros(N,2);
err_P(1,1)=P0(1,1);
err_P(1,2)=P0(2,2);
I=eye(2); %二维系统
for k=2:N
%物体下落,受状态方程的驱动
X(:,k)=A*X(:,k-1)+B*U+W(k);
%位移传感器对目标进行观测
Z(k)=H*X(:,k)+V(k);
%卡尔曼滤波
X_pre=A*Xkf(:,k-1)+B*U;%状态预测
P_pre=A*P0*A'+Q;%协方差预测
Kg=P_pre*H'*inv(H*P_pre*H'+R);%计算卡尔曼增益
Xkf(:,k)=X_pre+Kg*(Z(k)-H*X_pre);%状态更新
P0=(I-Kg*H)*P_pre;%方差更新
%误差均方值
err_P(k,1)=P0(1,1);
err_P(k,2)=P0(2,2);
end
%误差计算
messure_err_x=zeros(1,N);%位移的测量误差
kalman_err_x=zeros(1,N);%卡尔曼估计的位移与真实位移之间的偏差
kalman_err_v=zeros(1,N);%卡尔曼估计的速度与真实速度之间的偏差
for k=1:N
messure_err_x(k)=Z(k)-X(1,k);
kalman_err_x(k)=Xkf(1,k)-X(1,k);
kalman_err_v(k)=Xkf(2,k)-X(2,k);
end
%画图输出
%噪声图
figure
plot(V);
title('messure noise')
%位置偏差
figure
hold on,box on;
plot(messure_err_x,'-r.');%测量的位移误差
plot(kalman_err_x,'-g.');%卡尔曼估计位置误差
legend('测量误差','kalman估计误差')
figure
plot(kalman_err_v);
title('速度误差')
figure
plot(err_P(:,1));
title('位移误差均方值')
figure
plot(err_P(:,2));
title('速度误差均方值')7.2 卡尔曼滤波应用于小球落体运动目标跟踪
kalman.m
clear,clc
% compute the background image
Imzero = zeros(240,320,3);
for i = 1:5
Im{i} = double(imread(['DATA/',int2str(i),'.jpg']));
Imzero = Im{i}+Imzero;
end
Imback = Imzero/5;
[MR,MC,Dim] = size(Imback);
% Kalman filter initialization
R=[[0.2845,0.0045]',[0.0045,0.0455]'];%观察噪声方差
H=[[1,0]',[0,1]',[0,0]',[0,0]'];%观测矩阵
Q=0.01*eye(4);%状态转移协方差矩阵 eye(4)为4×4单位矩阵
P = 100*eye(4);%状态协方差矩阵
dt=1;
A=[[1,0,0,0]',[0,1,0,0]',[dt,0,1,0]',[0,dt,0,1]'];%状态转移矩阵F
g = 0; % pixels^2/time step
Bu = [0,0,0,g]';%控制矩阵
kfinit=0;
x=zeros(100,4);
% loop over all images
for i = 1 : 60
% load image
Im = (imread(['DATA/',int2str(i), '.jpg']));
imshow(Im)
imshow(Im)
Imwork = double(Im);
i
%extract ball
[cc(i),cr(i),radius,flag] = extractball(Imwork,Imback,i);
if flag==0
continue
end
hold on
for c = -1*radius: radius/20 : 1*radius
r = sqrt(radius^2-c^2);
plot(cc(i)+c,cr(i)+r,'g.')
plot(cc(i)+c,cr(i)-r,'g.')
end
% Kalman update
if kfinit==0
xp = [MC/2,MR/2,0,0]'
else
xp=A*x(i-1,:)' + Bu%【1】状态预测公式
end
kfinit=1;
PP = A*P*A' + Q%【2】不确定性在各个时刻间的传递关系
K = PP*H'*inv(H*PP*H'+R)%【3】卡尔曼系数
x(i,:) = (xp + K*([cc(i),cr(i)]' - H*xp))';%【4】状态更新
x(i,:)
a=[cc(i),cr(i)]
P = (eye(4)-K*H)*PP%噪声协方差矩阵的更新
hold on
for c = -1*radius: radius/20 : 1*radius
r = sqrt(radius^2-c^2);
plot(x(i,1)+c,x(i,2)+r,'r.')
plot(x(i,1)+c,x(i,2)-r,'r.')
end
pause(0.3)
end
% show positions
figure
plot(cc,'r*')
hold on
plot(cr,'g*')
%end
%estimate image noise (R) from stationary ball
posn = [cc(55:60)',cr(55:60)'];
mp = mean(posn);
diffp = posn - ones(6,1)*mp;
Rnew = (diffp'*diffp)/5;
%%%%%%%%%%%%%%%%
extractball.m
% extracts the center (cc,cr) and radius of the largest blob
function [cc,cr,radius,flag]=extractball(Imwork,Imback,index)%,fig1,fig2,fig3,fig15,index)
cc = 0;
cr = 0;
radius = 0;
flag = 0;
[MR,MC,Dim] = size(Imback);%背景的尺寸
% subtract background & select pixels with a big difference
fore = zeros(MR,MC); %image subtracktion
fore = (abs(Imwork(:,:,1)-Imback(:,:,1)) > 10) ...
| (abs(Imwork(:,:,2) - Imback(:,:,2)) > 10) ...
| (abs(Imwork(:,:,3) - Imback(:,:,3)) > 10);
% Morphology Operation erode to remove small noise
foremm = bwmorph(fore,'erode',2); %2 time%数学形态学消除小噪声
% select largest object
labeled = bwlabel(foremm,4);%四邻域标号
stats = regionprops(labeled,['basic']);%basic mohem nist
[N,W] = size(stats);%总共有N个目标在图像中
if N < 1%如果没有目标就返回
return
end
% do bubble sort (large to small) on regions in case there are more than 1排序
id = zeros(N);
for i = 1 : N
id(i) = i;
end
for i = 1 : N-1
for j = i+1 : N
if stats(i).Area < stats(j).Area%将stasts(各目标)按照从大到小的顺序排序
tmp = stats(i);
stats(i) = stats(j);
stats(j) = tmp;
tmp = id(i);
id(i) = id(j);
id(j) = tmp;%同样id中的标号为面积大到小的区域的标号
end
end
end
% make sure that there is at least 1 big region
if stats(1).Area < 100 %保证至少有一个足够大的区域
return%如果最大的区域面积都小于100,则返回
end
selected = (labeled==id(1));%selected为0、1矩阵,1对应着id(1)的目标,即面积最大的目标
% get center of mass and radius of largest
centroid = stats(1).Centroid;%最大目标的中心
radius = sqrt(stats(1).Area/pi);%最大目标的面积
cc = centroid(1);%
cr = centroid(2);
flag = 1;
return