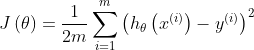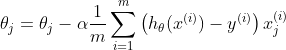吴恩达机器学习课后作业Python实现（一）：线性回归

目录

前言

单变量线性回归

代码实现

数据集准备

代价函数

梯度下降

跑模型并预测

绘制线性模型及代价函数图

 多元线性回归

代码实现

结果图

---

前言

        写本篇文章的主要目的是记录自己机器学习与Python的学习历程，

单变量线性回归

       在本部分的练习中，您将使用一个变量实现线性回归，以预测食品卡车的利润。假设你是一家餐馆的首席执行官，正在考虑不同的城市开设一个新的分店。该连锁店已经在各个城市拥有卡车，而且你有来自城市的利润和人口数据。 您希望通过使用这些数据来帮助您扩展到下一个城市；

代码实现

数据集准备

• 导入库

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

• 导入数据并且展示

# 数据路径
path = r'E:\Code\ML\ml_learning\ex1\ex1data1.txt'

# 读取数据
# names 添加列明，分别是人口，利润
# header 指定第几行作为列名
data = pd.read_csv(path, header=None, names=['Population', 'Profit'])
# 读取数据中的前五项数据，head()内不写时默认5，若输入4，则输出4行，9则输出9行数据，-1输出至倒数第二行数据，-11输出至倒数第12行数据
print(data.head())
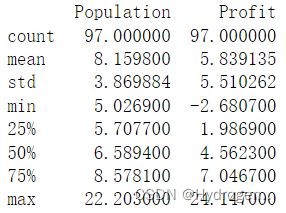
# 统计汇总数据的信息，如平均值，标准差， 最小值，最大值等
print(data.describe())

•  数据可视化

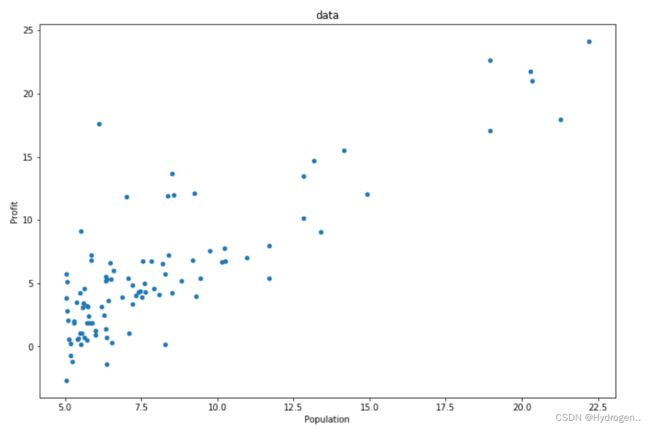
# 将数据可视化
# kind设置图标类型，scatter为散点图
# x，y为坐标轴标题
# figsize为打开窗口大小
# title为图标标题
data.plot(kind='scatter', x='Population', y='Profit', figsize=(12, 8), title='data')
plt.show()

•  数据集处理 

# 加入第一列，全为1，x0 = 1
data.insert(0, 'ones', 1)
# 获取数据列数
cols = data.shape[1]
# iloc根据位置索引选取数据， 先行后列，选取前两列作为输入向量
x = data.iloc[:, 0:cols - 1]  
# 最后一列作为目标向量
y = data.iloc[:, cols - 1:cols]  
# print(x.head())
# print(y.head())
# 转化为矩阵
X = np.matrix(x.values)
y = np.matrix(y.values)
theta = np.matrix([0, 0])  # 初始参数设为0

代价函数

• 公式

        其中 ：       

def computeCost(X, y, theta):
    '''
    作用：计算代价函数，向量化
    :param X: 输入矩阵
    :param y: 输出目标
    :param theta: parameters参数
    :return:
    '''

    inner = np.power(((X * theta.T) - y), 2)
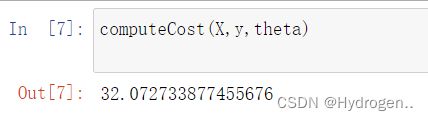
    return np.sum(inner) / (2 * len(X))

        当  和  = 0时，代价函数的初始值应为32.072733877455676

梯度下降

• 公式

        在这里我们使用向量化的形式来更新θ，可以大大提高效率

def gradientDescent(X, y, theta, alpha, epoch):
    '''
    作用: 梯度下降，获取最终theta值以及cost
    :param X: 输入矩阵
    :param y: 输出目标
    :param theta: 参数
    :param alpha: 学习率
    :param epoch: 迭代次数
    :return:
    '''

    # 初始化一个临时矩阵存临时参数
    temp_theta = np.matrix(np.zeros(theta.shape))
    # 获得参数的个数
    parameters_num = int(theta.flatten().shape[1])
    # 样本个数
    m = X.shape[0]
    # 获得每一轮训练的cost
    cost = np.zeros(epoch)
    # 记录每一轮的theta
    counterTheta = np.zeros((epoch, 2))
    for i in range(epoch):
        '''
        利用向量化计算，大大提高效率
        (97,2)*(2,1)->(97,1)->(1,97)*(97,2)=(1,2)
        '''
        temp_theta = theta - (alpha / m) * (X * theta.T - y).T * X
        theta = temp_theta  # 更新梯度
        counterTheta[i] = theta  # 记录每一次的theta
        cost[i] = computeCost(X, y, theta)  # 计算J(theta)并保存
    return counterTheta, theta, cost

跑模型并预测

        在这里学习率设置为0.01，训练次数设置为3800次

# 学习率
alpha = 0.01
# 训练次数
epoch = 3800
# 调用先前定义的两个函数
counterTheta, final_theta, cost = gradientDescent(X, y, theta, alpha, epoch)
computeCost(X, y, final_theta)

# 预测35000和70000城市规模的小吃摊利润
predict1 = [1, 3.5] * final_theta.T
print("predict1:", predict1)
predict2 = [1, 7] * final_theta.T
print("predict2:", predict2)

        得到预测如下

predict1: [[0.28255134]]

predict2: [[4.45669707]]

绘制线性模型及代价函数图

# np.linspace()
# 返回在区间[`start`，`stop`]中计算出的num个均匀间隔的样本
x = np.linspace(start=data.Population.min(), stop=data.Population.max(), num=100)  # xlabel横坐标
h = final_theta[0, 0] + final_theta[0, 1] * x  # ylabel profit

figure, ax = plt.subplots(nrows=1, ncols=2)
# 线性回归图
ax[0].plot(x, h, 'r', label='Prediction')
ax[0].scatter(data.Population, data.Profit, label='Training Data')
ax[0].legend(loc=2)
ax[0].set_xlabel('Population')
ax[0].set_ylabel('Profit')
ax[0].set_title('Predicted Profit vs. Population Size')
# 损失函数图
ax[1].plot(np.arange(epoch), cost, 'r')
ax[1].set_xlabel('Iteration')
ax[1].set_ylabel('Cost')
ax[1].set_title('Error vs. Training Epoch')
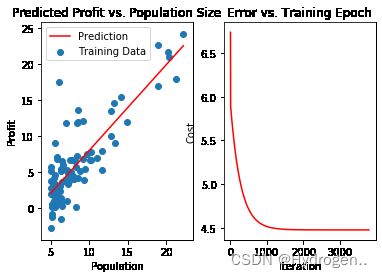
plt.show()

        得到拟合数据图和代价图如下，可知拟合程度比较好。

---

多元线性回归

        这里使用的数据是ex1data2，是多维数据，其中有2个变量（房子的大小，卧室的数量）1个目标（房子的价格），这里的代码与单变量线性回归的代码大同小异，由于特征值之间差距过大，故在预处理的时候我们需要将特征值归一化，以便使得模型更快的收敛。

        下面直接放代码和结果图

代码实现

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

'''
多变量线性回归
'''
# 数据路径
path = r'E:\Code\ML\ml_learning\ex1\ex1data2.txt'

# 读取数据
# names 添加列明，分别是面积 数量 价格
# header 指定第几行作为列名
data = pd.read_csv(path, header=None, names=['Size', 'Bedrooms', 'Price'])
# 特征归一化
data = (data - data.mean()) / data.std()
# 加入第一列，全为1，x0 = 1
data.insert(0, 'ones', 1)
# 获取数据列数
cols = data.shape[1]
# iloc根据位置索引选取数据， 先行后列，选取前两列作为输入向量
x = data.iloc[:, 0:cols - 1]
# 最后一列作为目标向量
y = data.iloc[:, cols - 1:cols]
# 转化为矩阵
X = np.matrix(x.values)
y = np.matrix(y.values)
theta = np.matrix([0, 0, 0])  # 初始参数设为0

'''
代价函数
'''


def computeCost(X, y, theta):
    '''
    作用：计算代价函数，向量化
    :param X: 输入矩阵
    :param y: 输出目标
    :param theta: parameters参数
    :return:
    '''

    inner = np.power(((X * theta.T) - y), 2)
    return np.sum(inner) / (2 * len(X))


'''
梯度下降
'''


def gradientDescent(X, y, theta, alpha, epoch):
    '''
    作用: 梯度下降，获取最终theta值以及cost
    :param X: 输入矩阵
    :param y: 输出目标
    :param theta: 参数
    :param alpha: 学习率
    :param epoch: 迭代次数
    :return:
    '''

    # 初始化一个临时矩阵存临时参数
    temp_theta = np.matrix(np.zeros(theta.shape))
    # 获得参数的个数
    parameters_num = int(theta.flatten().shape[1])
    # 样本个数
    m = X.shape[0]
    # 获得每一轮训练的cost
    cost = np.zeros(epoch)
    # 记录每一轮的theta
    counterTheta = np.zeros((epoch, 3))
    for i in range(epoch):
        '''
        利用向量化计算，大大提高效率
        (97,2)*(2,1)->(97,1)->(1,97)*(97,2)=(1,2)
        '''
        temp_theta = theta - (alpha / m) * (X * theta.T - y).T * X
        theta = temp_theta  # 更新梯度
        counterTheta[i] = theta  # 记录每一次的theta
        cost[i] = computeCost(X, y, theta)  # 计算J(theta)并保存
    return counterTheta, theta, cost


'''
跑模型，画图
'''
# 学习率
alpha = 0.01
# 训练次数
epoch = 3800
# 调用先前定义的两个函数
counterTheta, final_theta, cost = gradientDescent(X, y, theta, alpha, epoch)
computeCost(X, y, final_theta)

fig2, ax = plt.subplots(figsize=(8, 4))
ax.plot(np.arange(epoch), cost, 'r')
ax.set_xlabel('Iteration')
ax.set_ylabel('Cost')
ax.set_title('Error vs. Training Epoch')
plt.show()

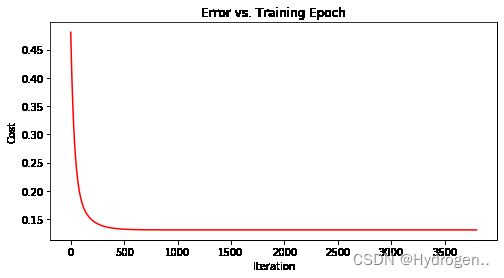
结果图

 参考链接

https://blog.csdn.net/weixin_48577398/article/details/117134767?spm=1001.2014.3001.5502

https://www.heywhale.com/mw/project/5da16a37037db3002d441810