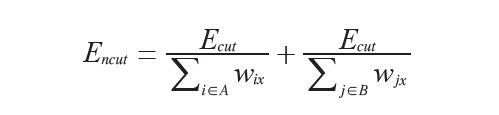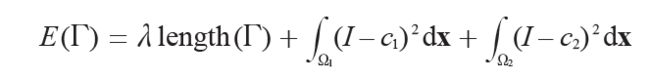python计算机视觉学习第9章——图像分割

目录

引言

一、图割(Graph Cut)

1.1 从图像创建图 

1.2 用户交互式分割

二、 利用聚类进行分割 

三、 变分法

---

引言

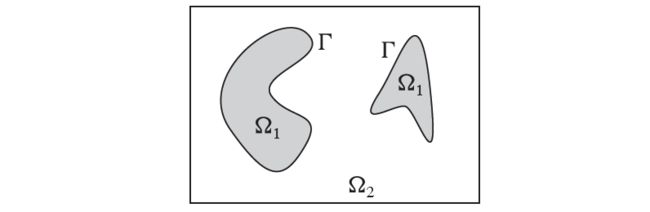
        图像分割是将一幅图像分割成有意义区域的过程。区域可以是图像的前景与背景或图像中一些单独的对象。这些区域可以利用一些诸如颜色、边界或近邻相似性等特征进行构建。

一、图割(Graph Cut)

        图是由若干个节点和连接节点的边构成的集合。边可以是有向的或是无向的并且这些可能有与它们相关联的权重。

        图割是将一个有向图像分割成两个互不相交的集合，可以用来解决很多计算机视觉方面的问题。其基本思想是，相似且彼此相近的像素应该划分到同一区域。

        图割C(C是图中所有边的集合)的“代价”函数定义为所有割的边的权重求和相加：

是图中节点i到节点j的边(i,j)的权重，且是对割C所有的边进行求和。

        图割图像分割的思想是用图来表示图像，并对图进行划分以使割代价最小，用图表示图像时，增加两个额外的节点，源点和汇点，并仅考虑那些将源点和汇点分开的割。寻找最小的割等同于在源点和汇点之间寻找最大流/最小割的问题。

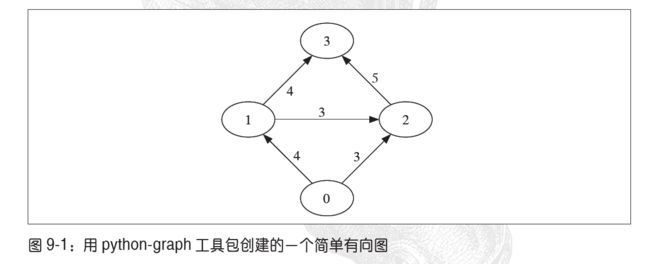
        这里的图割例子中将采用python-graph工具包，需要另外下载，我在pycharm中并未找到这个工具包，因此在https://github.com/pmatiello/python-graph中下载了python-graph-master文件，将其复制到项目文件下即可。

这里是使用工具包计算一幅较小图的最大流/最小割的例子：

from pygraph.classes.digraph import digraph
from pygraph.algorithms.minmax import maximum_flow

gr = digraph()
gr.add_nodes([0, 1, 2, 3])
gr.add_edge((0, 1), wt=4)
gr.add_edge((1, 2), wt=3)
gr.add_edge((2, 3), wt=5)
gr.add_edge((0, 2), wt=3)
gr.add_edge((1, 3), wt=4)
flows,cuts = maximum_flow(gr, 0, 3)
print('flow is:', flows)
print('cut is', cuts)

创建有4个节点的有向图，4个节点的索引为0-3，用add_edge()增添边并为每条边指定特定权重，打印来的结果如下：

1.1 从图像创建图 

        给定一个邻域结构，就可以利用图像像素作为节点定义一个图。一个四邻域指一个像素与其正上方、正下方、左边、右边的像素直接相连。

        除像素节点以外还需两个特定的节点——源点与汇点，代表图像的前景和背景。利用简单模型将其连接起来。

        下面是创建这样一个图的步骤:

        1、每个像素节点都有一个从源点的传入边

        2、每个像素节点都有一个到汇点的传出边

        3、每个像素节点都有一条传入边和传出边连接到它的近邻

分割模型可以帮助确定边的权重，像素i到像素j之间的边的权重就记为，源点到像素i的权重记为，像素i到汇点之间的权重记为.

为边的权重创建如下模型：

利用该模型，将每个像素和前景及背景连接起来，权重等于上面归一化后的概率。其中表示了近邻间像素的相似性，相似像素权重趋近于，不相似的趋近于0，参数则表示了随着不相似性的增加，指数次幂衰减到0的快慢。

        下面为从一幅图像创建图的函数：

from pylab import *
from numpy import *
from PCV.classifiers import bayes
from pygraph.classes.digraph import digraph
from pygraph.algorithms.minmax import maximum_flow


def build_bayes_graph(im, labels, sigma=1e2, kappa=2):

    """ 从像素四邻域建立一个图，前景和背景（前景用 1 标记，背景用 -1 标记，其他的用 0 标记）由 labels 决定，并用朴素贝叶斯分类器建模 """
    m, n = im.shape[:2]
    #每行是一个像素的 RGB 向量
    vim = im.reshape((-1, 3))
    # 前景和背景（RGB）
    foreground = im[labels == 1].reshape((-1, 3))
    background = im[labels == -1].reshape((-1, 3))
    train_data = [foreground, background]
    # 训练朴素贝叶斯分类器
    bc = bayes.BayesClassifier()
    bc.train(train_data)
    #  获取所有像素的概率
    bc_lables, prob = bc.classify(vim)
    prob_fg = prob[0]
    prob_bg = prob[1]
    # 用 m * n +2 个节点创建图
    gr = digraph()
    gr.add_nodes(range(m * n + 2))
    source = m * n  # 倒数第二个是源点
    sink = m * n + 1  # 最后一个节点是汇点
    # 归一化
    for i in range(vim.shape[0]):
        vim[i] = vim[i] / (linalg.norm(vim[i]) + 1e-9)
        # 遍历所有的节点，并添加边
    for i in range(m * n):
        # 从源点添加边
        gr.add_edge((source, i), wt=(prob_fg[i] / (prob_fg[i] + prob_bg[i])))
    # 向汇点添加边
    gr.add_edge((i,sink), wt=(prob_bg[i]/(prob_fg[i]+prob_bg[i])))
    # 向相邻点添加边，
    if i%n != 0:  # 左边存在
        edge_wt = kappa*exp(-1.0*sum((vim[i]-vim[i-1])**2)/sigma)
        gr.add_edge((i,i-1),wt=edge_wt)
    if (i+1)%n != 0:  # 右边存在
        edge_wt = kappa*exp(-1.0*sum((vim[i]-vim[i-1])**2)/sigma)
        gr.add_edge((i,i+1),wt=edge_wt)
    if i//n != 0:  # 上边存在
        edge_wt = kappa*exp(-1.0*sum((vim[i]-vim[i-1])**2)/sigma)
        gr.add_edge((i,i-n),wt=edge_wt)
    if i//n != m-1:  # 左边存在
        edge_wt = kappa*exp(-1.0*sum((vim[i]-vim[i-1])**2)/sigma)
        gr.add_edge((i,i+n),wt=edge_wt)
    return gr

用1标记前景训练数据，-1标记背景训练数据的一幅标记图像。基于这种标记在RGB值上可以训练除一个朴素贝叶斯分类器，之后计算每一个像素的分类概率，这些计算除的分类概率便是从源点出来到汇点取的边的权重。根据这些创建一个节点为n*m+2的图。

实验代码：

from PIL import Image

from pylab import *
from numpy import *
from skimage.transform import resize
import graphcut

im = array(Image.open('D:\\picture\\test_img0\\tem1.jpg'))
im = resize(im, (50,50))
size = im.shape[:2]

# 添加两个矩形训练区域
labels = zeros(size)
labels[3:18,3:18] = -1
labels[-18:-3,-18:-3] = 1
# 创建图
g = graphcut.build_bayes_graph(im, labels, kappa=2)
# 对图像进行分割
res = graphcut.cut_graph(g, size)
figure()
graphcut.show_labeling(im,labels)
figure()
imshow(res)
gray()
axis('off')
show()

        为了在图像上可视化覆盖的标记区域，利用contourf()函数填充图像等高线间的区域，参数alpha用于设置透明度。

1.2 用户交互式分割

        利用一些方法可以将图割分割与用户交互结合起来，用户可以在一幅图像上为前景和背景提供一些标记。另一种就可以利用边界框选择一个包含前景的区域。

        这里使用的图像是书中用的数据集图像，可以帮助评价分割性能的真实标记，并模拟用户选择矩形图像区域或用‘lasso’之类的工具来标记前景和背景的标注信息。

        将用户输入编码成具有以下意义的位图图像：       

像素值	意义
0.64	背景
128	未知
255	前景

from numpy import *
from scipy.misc import imresize
import graphcut
def create_msr_labels(m,lasso=False):
    """ 从用户的注释中创建用于训练的标记矩阵 """
    labels = zeros(im.shape[:2])
    # 背景
    labels[m==0] = -1
    labels[m==64] = -1
    #前景
    if lasso:
        labels[m == 255] = 1
    else:
        labels[m == 128] = 1
    return labels
    # 载入图像和注释图
im = array(Image.open('D:\\picture\\test4.jpg'))
m = array(Image.open('D:\\picture\\test4.bmp'))
# 调整大小
scale = 0.1
im = resize(im, scale, interp='biliner')
m = resize(m, scale, interp='nearest')
# 创建训练标记
labels = create_msr_labels(m,False)
# 用注释创建图
g = graphcut.build_bayes_graph(im, labels, kappa=1)
# 图割
res = graphcut.cut_graph(g, im.shape[:2])
# 去除背景部分
res[m==0] = 1
res[m==64] = 1
# 绘制分割结果
figure()
imshow(res)
gray()
xticks([])
yticks([])
savefig('D:\\picture\\library.pdf')

由于scipy.misc版本的问题未能输出图像这里借用师兄的图像：

通过定义一个辅助函数用以读取这些标注图像，格式化这些标注图像便于将其传递给背景和前景训练模型函数，矩形框中只包含背景标记。上图中显示了利用RGB向量作为原始图像的特征进行分割的一些结果，一个下采样掩膜和下采样分割结果。

二、 利用聚类进行分割 

        上面的图割问题通过在图像的图上利用最大流/最小割找到了一种离散的解决方法。这这里将使用基于谱图理论的归一化分割算法，将像素相似和空间相似结合起来对图像进行分割。

        这个方法来自定义一个分割损失函数，该损失函数不仅考虑了组的大小还用划分的大小对该损失函数进行“归一化”。归一化后为：

A，B表示两个割集，并于图中分别对A和B中所有其他节点的权重进行求和相加。 定义W为变得权重，矩阵中的元素为连接像素i和像素j边的权重。D为对w每行元素求和后构成的对角矩阵即。归一化分割可以通过最小化下面的优化问题而求得：

y包含的是离散标记，这些离散标记满足对于b为常数的约束。

通过松弛约束条件并让y取任意实数，该问题可以变为一个容易求解的特征分解问题，缺点是需要对输出设置阈值或进行聚类，使其重新称为一个离散分割。

松弛这个问题后，就成为了求解拉普拉斯矩阵特征向量的问题：

连接像素i和像素j的边的权重就为：

第一部分度量像素之间的像素相似性，定义为RGB向量或灰度值。第二部分度量图像中的接近程度，定义为每个像素的坐标矢量。在代码中体现如下：

def ncut_graph_matrix(im,sigma_d=1e2,sigma_g=1e-2):
    """  创建用于归一化割的矩阵，其中sigma_d和sigma_g是像素距离和像素相似性的权重参数"""
    
    m,n = im.shape[:2] 
    N = m*n
    
    # 归一化，并创建RGB或灰度特征向量
    if len(im.shape)==3:
        for i in range(3):
            im[:,:,i] = im[:,:,i] / im[:,:,i].max()
        vim = im.reshape((-1,3))
    else:
        im = im / im.max()
        vim = im.flatten()
    
    # x,y坐标用于距离计算
    xx,yy = meshgrid(range(n),range(m))
    x,y = xx.flatten(),yy.flatten()
    
    # 创建边线权重矩阵
    W = zeros((N,N),'f')
    for i in range(N):
        for j in range(i,N):
            d = (x[i]-x[j])**2 + (y[i]-y[j])**2 
            W[i,j] = W[j,i] = exp(-1.0*sum((vim[i]-vim[j])**2)/sigma_g) * exp(-d/sigma_d)
    
    return W

函数用于获取图像数组，并利用输入的彩色图像RGB值或灰度图像的灰度值创建一个特征向量。对于每个像素的特征向量，利用meshgrid()函数来获取x和y值，之后函数会在N个像素上循环，并在N*N归一化割矩阵W中填充值。

聚类过程的实现:

def cluster(S,k,ndim):
    """ 从相似性矩阵进行谱聚类"""
    
    # 检查对称性
    if sum(abs(S-S.T)) > 1e-10:
        print ('not symmetric')
    
    # 创建拉普拉斯矩阵
    rowsum = sum(abs(S),axis=0)
    D = diag(1 / sqrt(rowsum + 1e-6))
    L = dot(D,dot(S,D))
    
    # 计算L的特征向量
    U,sigma,V = linalg.svd(L,full_matrices=False)
    
    # 从前ndim个特征向量创建特征向量
    # 堆叠特征向量作为矩阵的列
    features = array(V[:ndim]).T

    # k-means
    features = whiten(features)
    centroids,distortion = kmeans(features,k)
    code,distance = vq(features,centroids)
        
    return code,V

采用的基于特征向量图像值的K-means聚类算法，对像素进行分组，下面为利用该算法进行的实验：

from PIL import Image
from PCV.tools import ncut
from pylab import *
from numpy import *

def scipy_misc_imresize(arr, size, interp='bilinear', mode=None):
   im = Image.fromarray(arr, mode=mode)
   ts = type(size)
   if np.issubdtype(ts, np.signedinteger):
      percent = size / 100.0
      size = tuple((np.array(im.size)*percent).astype(int))
   elif np.issubdtype(type(size), np.floating):
      size = tuple((np.array(im.size)*size).astype(int))
   else:
      size = (size[1], size[0])
   func = {'nearest': 0, 'lanczos': 1, 'bilinear': 2, 'bicubic': 3, 'cubic': 3}
   imnew = im.resize(size, resample=func[interp]) # 调用PIL库中的resize函数
   return np.array(imnew)


im = array(Image.open("D:\\picture\\C-uniform01.ppm"))
m,n = im.shape[:2]

#调整图像的尺寸大小为（wid,wid）
wid = 50
rim = scipy_misc_imresize(im, (wid,wid), interp='bilinear')
rim = array(rim, 'f')

#创建归一化割矩阵
A = ncut.ncut_graph_matrix(rim,sigma_d=1,sigma_g=1e-2)

#聚类
code,V = ncut.cluster(A,k=3,ndim=3)

#变换到原来的图像大小
codeim = scipy_misc_imresize(code.reshape(wid,wid), (m,n), interp='nearest')

#绘制分割结果
figure()
subplot(121)
imshow(im)
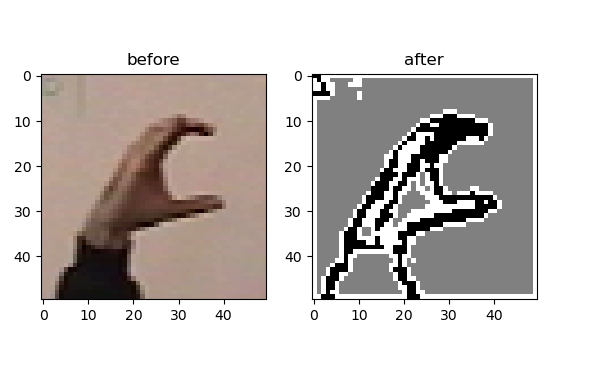
title('before')
subplot(122)
imshow(codeim)
title('after')
gray()
show()

因为numpy中的linanlg,svd()函数在处理大型矩阵时计算方法并不快，所以重新设定图像为固定尺寸。这个例子里使用的是gesture数据库里的一幅图像分割结果如下图所示：

三、 变分法

        诸如ROF降噪、K-means和SVM都是优化的问题，当优化对象是函数时，该问题又被称为变分问题，解决这类问题是算法就被称为变分法。

Chan-Vese分割模型对于待分割图像区域假定一个分片常数图像模型。集中注意前景和背景两个区域的情形。如果用一组曲线将图像分割成两个区域，分割是通过最小化Chan-Vese模型能量函数给出的：

用于度量与内部平均灰度常数和外部平均灰度常数的偏差。

        由分片常数图像 ，可将上式重写为：

是两区域 的特征函数。

将最小化Chan-Vese模型现在转变为设定阈值的ROF降噪问题：

from PIL import Image
from PCV.tools import rof
from pylab import *
import imageio

im = array(Image.open("D:\\picture\\boy_on_hill.jpg").convert('L'))
U, T = rof.denoise(im,im,tolerance=0.01)
t = 0.4  #阈值
title('Original Image')
imshow(im)

imageio.imsave('result.pdf', U < t*U.max())

因为imsave的弃用这里查找资料后使用了上面的方法，但是还是出现了错误：

具体原因目前还不清楚，有待进一步处理。