卷积与转置卷积的关系，pytorch里的转置卷积(反卷积)ConvTranspose2d的计算过程图解及转置卷积计算公式理解

前言

在我们用深度学习做图像处理需要上采样操作时，目前比较常用的两种上采样方式
一是转置卷积
二是PixelShuffle
这里先谈一下转置卷积的实现过程。谈到转置卷积肯定得与卷积联系起来，在pytorch中卷积类的参数如下：

torch.nn.Conv2d(in_channels, out_channels, kernel_size, stride=1, padding=0, dilation=1, groups=1, bias=True, padding_mode='zeros', device=None, dtype=None)

这些都是我们很熟悉的卷积参数：

• in_channels：输入的通道数
• out_channels：输出的通道数
• kernel_size：卷积核大小
• stride：步长
• padding：对输入进行填充
• dilation：卷积核的空洞
• groups：卷积的分组
• bias：卷积结果后添加的偏置
• padding_mode：填充的类型

在pytorch中转置卷积的类torch.nn.ConvTranspose2d参数如下：

torch.nn.ConvTranspose2d(in_channels, out_channels, kernel_size, stride=1, padding=0, output_padding=0, groups=1, bias=True, dilation=1, padding_mode='zeros', device=None, dtype=None)

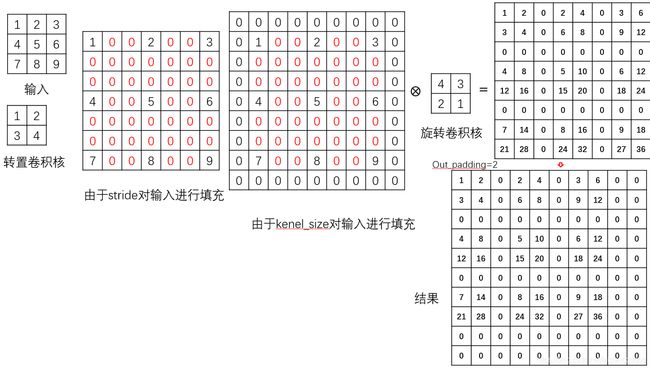
可以看到pytorch中转置卷积的参数与卷积的参数一模一样！说明它们之间肯定是有联系的，在进行转置卷积操作时首先对输入的每行每列之间填充(stride-1)行(列)的0，然后再对填充的输入的外围填充(kernel_size-1)圈的0，然后再用旋转180°的卷积核对填充后的输入进行步长为1卷积，如果padding不等于0，则对卷积后的结果的外围进行去除padding圈，如果output_padding不等于0，则还需要对最后的结果右侧和下方填充output_padding的0.下面用图形来详细说明转置卷积的计算过程。

转置卷积图解

为了更好的验证结果的正确性，这里用torch.nn.functional.conv_transpose2d来进行结果的验证。

torch.nn.functional.conv_transpose2d(input, weight, bias=None, stride=1, padding=0, output_padding=0, groups=1, dilation=1) → Tensor

这里主要讨论kernel_size，stride，padding与output_padding对转置卷积结果的影响。

卷积核大小对转置卷积的影响

卷积核大小对转置卷积的影响主要是对输入的填充多少圈0——(kernel_size-1)圈
下面通过对kernel_size=2和kernel_size=3来进行验证。

kernel_size=2，stride=1，padding=0，output_padding=0

下面是用于转置卷积的输入与卷积核及转置卷积后的结果：
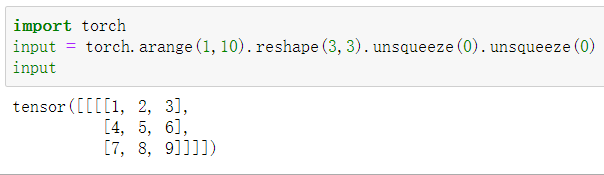
输入

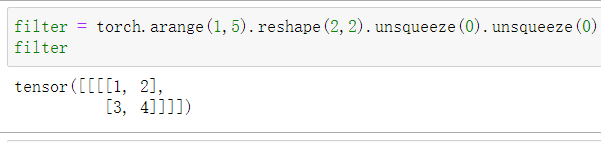
转置卷积核

结果

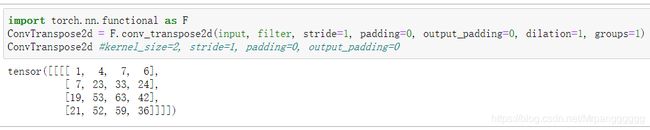
图形解释其过程：由于卷积核的大小为2，所以先对输入外围填充2-1=1圈的0，然后用旋转180°的卷积核对填充后的结果进行常规卷积(步长始终为1)操作。

kernel_size=3，stride=1，padding=0，output_padding=0

输入还是和之前一样，转置卷积核为下图所示：

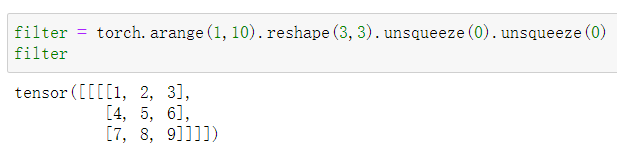
转置卷积的输出结果：

图形解释其过程：由于卷积核的大小为3，所以先对输入外围填充3-1=2圈的0，然后用旋转180°的卷积核对填充后的结果进行常规卷积操作(步长始终为1)。

padding对转置卷积结果的影响

padding对转置卷积结果的影响主要体现在对转置卷积得到的结果进行去除

kernel_size=3，stride=1，padding=1，output_padding=0

输入

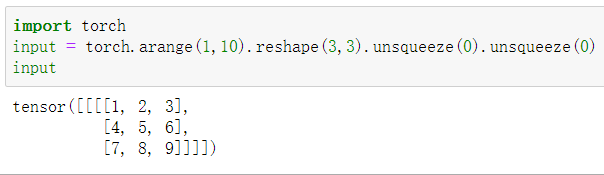
转置卷积核

结果

图形解释其过程：由于卷积核的大小为3，所以先对输入外围填充3-1=2圈的0，然后用旋转180°的卷积核对填充后的结果进行常规卷积操作(步长始终为1)，又由于padding=1，所以对卷积得到的结果的最外一层去掉（这正好与卷积里的padding的用法相反，卷积里的padding是对输入进行填充）。

kernel_size=3，stride=1，padding=2，output_padding=0

输入和卷积核还是和上面一样，只是将padding设为2.
结果

图形解释其过程：由于卷积核的大小为3，所以先对输入外围填充3-1=2圈的0，然后用旋转180°的卷积核对填充后的结果进行常规卷积操作(步长始终为1)，又由于padding=2，所以对卷积得到的结果的最外两层去掉。

步长stride对转置卷积结果的影响

步长stride对转置卷积的影响主要体现在对输入进行0填充，输入的每行每列之间填充stride-1的0.
输入

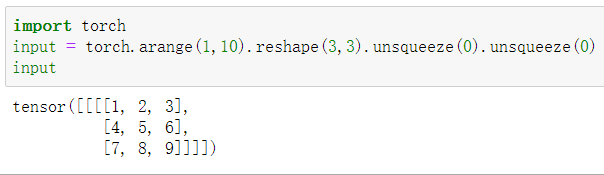
转置卷积核

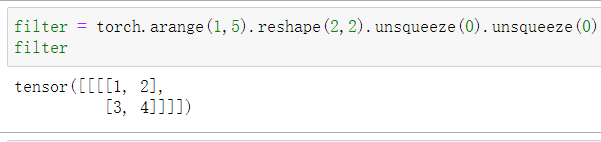
kernel_size=2，stride=2，padding=0，output_padding=0的结果

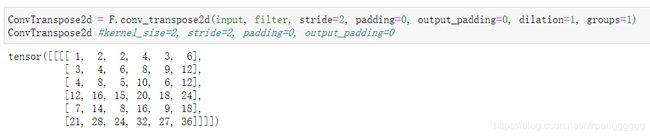
图形解释其过程：由于步长stride=2，则需对输入的每行每列之间填充2-1=1的0。又由于卷积核的大小为2，所以还需对输入外围填充2-1=1圈的0，然后用旋转180°的卷积核对填充后的结果进行常规卷积操作(步长始终为1)。

kernel_size=2，stride=3，padding=0，output_padding=0的结果

图形解释其过程：由于步长stride=3，则需对输入的每行每列之间填充3-1=2的0。又由于卷积核的大小为2，所以还需对输入外围填充2-1=1圈的0，然后用旋转180°的卷积核对填充后的结果进行常规卷积操作(步长始终为1)。

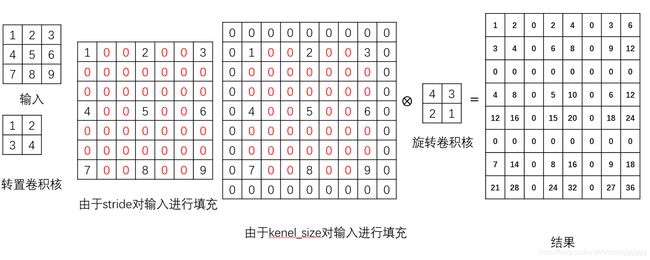
out_padding对转置卷积结果的影响——对输出填充0

out_padding对转置卷积的影响是对卷积得到的结果的右侧和下方进行0填充（注意stride的大小必须大于out_padding的大小）
输入

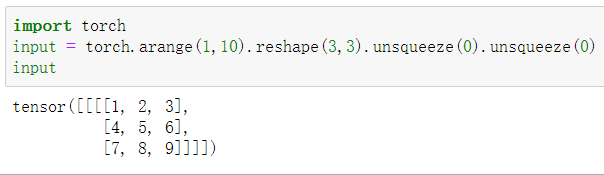
转置卷积核

kernel_size=2，stride=2，padding=0，output_padding=1的结果

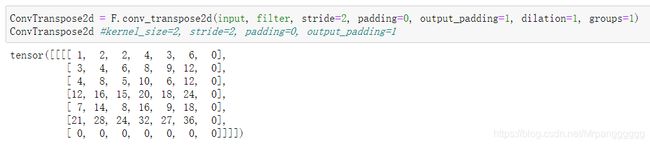
图形解释其过程：由于步长stride=2，则需对输入的每行每列之间填充2-1=1的0。又由于卷积核的大小为2，所以还需对输入外围填充2-1=1圈的0，然后用旋转180°的卷积核对填充后的结果进行常规卷积操作(步长始终为1)，又由于out_padding=1，所以还需对卷积得到的结果的右侧和下方进行1列/行的0填充。

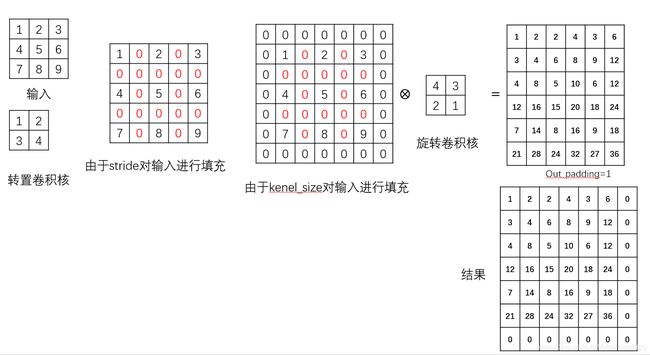
kernel_size=2，stride=3，padding=0，output_padding=2的结果

输入和卷积核还是和上面一样，不过由于stride的大小必须大于out_padding的大小，所以stride设为3.输出如下

图形解释其过程：由于步长stride=2，则需对输入的每行每列之间填充2-1=1的0。又由于卷积核的大小为2，所以还需对输入外围填充2-1=1圈的0，然后用旋转180°的卷积核对填充后的结果进行常规卷积操作(步长始终为1)，又由于out_padding=2，所以还需对卷积得到的结果的右侧和下方进行2列/行的0填充。

转置卷积计算公式理解

有了上面的分析，对pytorch官方文档给出的转置卷积的计算公式就不难理解了。
假设输入的大小为$H\times W$，这里只考虑对$H$的影响，首先，由于参数sttride的影响需要对输入的每行每列之间填充(stride-1)行或列的0，则输入$H$的大小变为$H+(stride-1)\times (H-1)=(H-1)\times stride+1$，又由于参数kernel_size的影响需要对输入的外围填充$kernel\_size-1$圈的0，则输入的大小变为$(H-1)\times stride+1+2\times (kernel\_size-1)$，接下来进行的是步长为1的常规卷积操作，则由卷积的计算公式有：$(H-1)\times stride+1+2\times (kernel\_size-1)-kernel\_size+1=(H-1)\times stride+1+(kernel\_size-1)$，由于padding与out_padding的存在需要对卷积后结果的去除或填充，则：
$(H-1)\times stride+1+(kernel\_size-1)-2\times padding+out\_padding$.这就是pytorch官方文档给的转置卷积计算公式，当然这里没考虑dilation.

总结

这篇文章主要说明了转置卷积里的参数kernel_size, stride, padding, out_padding对转置卷积结果的影响。其中前两个参数影响输入的填充，后两个参数影响卷积后结果的去除或填充。总之，转置卷积还是卷积，只不过对输入和输出进行某些处理而已。