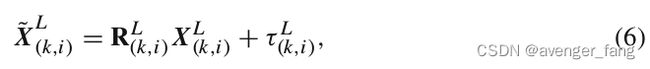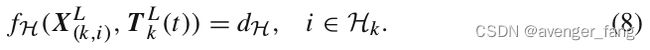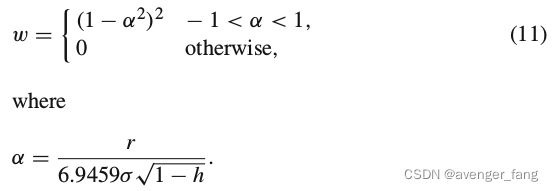LOAM论文精读
《Low-drift and real-time lidar odometry and mapping》
概要
论文提出了一种使用3D激光雷达在移动中实时实现低漂移6-DOF里程计和建图的方法。这个问题很困难,因为激光距离测量是在不同的时间接收到的,而且运动估计的误差(特别是没有外部参考,如GPS)会导致结果点云的配准错误。实现这种方法的关键思想是分级策略,使用一种算法在高频但低保真度下执行里程计来估计激光雷达的速度。虽然不一定必须要IMU,但如果IMU可用,它可以提供一个运动先验和减轻剧烈的,高频运动;第二种算法以较低数量级的频率运行于点云的精细匹配和配准。这两种算法的结合允许实时创建地图。
1 Introduction
如果激光传感器唯一的运动是对已知激光雷达的内部运动学的激光束的指向,则简单地得到这个配准。然而,如果传感器底座移动,如在许多感兴趣的应用中,激光点配准与内部运动学和外部运动有关。 第二种对每一次的测量必须包含传感器如何确定位置和姿态的理论。由于激光可以每秒测量几十万次的距离,高速率的姿态估计是一个重要的问题。解决这一问题的一种常见方法是使用一种独立的姿态估计方法(例如使用一个精确的GPS/INS系统),参照一个固定的坐标系,将测量的数据配准到一个在相对固定坐标系的另一个坐标系对应点云中。当相对于固定坐标系的独立测量是不可用的时,通常所使用的技术是使用某种里程计估计来配准点,例如使用车轮运动、陀螺仪的组合,以及通过跟踪雷达测量或视觉图像中的特征。
在这里,我们考虑使用在6-DOF中移动的机械扫描激光测距装置来(可选择使用低频率的IMU等惯性测量传感器)创建地图的情况。只使用激光测距的一个关键优点是,它对场景中的环境照明或光学纹理不敏感。
由于我们试图将里程计推向实时尽可能最低的漂移,不要考虑与闭环相关的问题。事实上,虽然闭环可以帮助进一步消除漂移,但我们发现,在许多实际情况下,如绘制建筑物的楼层地图,闭环并不一定是必要的。
我们的方法,即LOAM,在6-DOF位姿估计中实现低漂移和低计算复杂度。使这种性能水平成为可能的关键思想是将SLAM问题划分为两种算法,旨在同时优化大量变量。 一种算法在高频但低保真度下实现里程计估计,以估计激光雷达在环境中移动的速度,来实现点云去畸变。虽然没有必要,但如果一个IMU是可用的,它可以提供一个运动先验,并帮助减轻剧烈,高频的运动估计。第二种算法以较低数量级的频率运行于点云的精细匹配和配准。具体来说,两种算法都提取位于边缘特征和平面上的特征点特征,并将特征点分别与边缘线段和平面小块进行匹配。在里程计算法中,通过找到特征点的对应关系来保证快速计算,而在建图算法中,通过特征匹配来保证精度,它们的作用是不同的。
该方法首先解决了一个较简单的问题,即在线速度估计,然后将建图进行批量优化,得到高精度的运动估计和建图。并行算法的结构保证了能够实时解决问题的可行性。此外,由于运动估计是在更高的频率下进行的,建图被给予足够的时间来提高精度。当建图过程交错运行比里程计估计算法慢一个数量级时,建图算法包含了大量的特征点,并使用了足够多次的迭代来收敛。本文的主要贡献如下:
(1)我们提出了一个利用双层优化在线估计自我运动和构建地图的软件系统;
(2)我们精心实现几何特征检测和匹配,以满足系统的要求:
(3)里程计算法中的特征匹配粗糙而快速,以确保高频,建图算法精确而缓慢,以确保低漂移;
(4)我们用覆盖不同类型环境的大量数据集对该方法进行了彻底的测试;我们尝试在详细的呈现我们的工作,允许读者复现该方法。
2 Related work
激光雷达已成为机器人导航中一种有用的测距传感器。对于定位和建图,一种方法是通过停止然后扫描,以避免点云中的运动失真(Nuchter等2007)。此外,当激光雷达的扫描频率高于其外部运动时,运动失真可以忽略。在这种情况下,ICP方法(Pomerleau等)可用于配准不同扫描帧之间的激光。此外,(Hong等2010)还提出了一种两步消除畸变的方法:先使用基于ICP的速度估计步骤之后,再使用计算的速度进行失真补偿步骤,去畸变之后再用它计算速度。一种类似的技术也被用来补偿由单轴三维激光雷达引入的畸变(Moosmann和Stiller2011)。
但是,如果扫描运动相对较慢,运动畸变可能会很严重。当使用2轴激光雷达时尤其如此,因为一个轴通常比另一个轴要慢得多。通常,其他传感器被用来提供速度测量,这样就可以消除失真。例如,激光雷达云可以通过与IMU集成的视觉里程计进行状态估计来配准(Scherer等2012)。当多个传感器,如GPS/INS和车轮编码器同时可用时,这个问题通常可以通过卡尔曼滤波器或粒子滤波器来解决,从而实时构建地图。
如果使用2轴激光雷达而没有得到其他传感器的帮助,运动估计和畸变校正就成为一个问题。在巴福特等人的方法中,传感器的运动被建模为恒速模型。Rosen等人使用高斯过程对连续传感器运动进行建模,并将问题表述为因子图优化问题(Rosen等2014)。此外,furgale等人建议使用b样条函数来模拟传感器的运动(Furgale等2012)。我们的方法使用了一个类似的线性运动模型(Dong和巴foot(2012)、安德森和巴福特(2013a)在里程计算法中使用的模型)。而在建图算法中,则采用了刚体变换。另一种方法是Bosse和Zlot(Bosse和Zlot2009、Bosse等2012年、Zlot和Bosse等2012年)。他们发明了一种名为Zebedee的3D测绘设备,由2D激光雷达和通过弹簧连接到手杆上的IMU组成(Bossee人。2012).建图是通过手动“点头”式操作的设备来进行的。通过批处理优化方法,处理分割数据集之间添加边界约束的段。在该方法中,使用IMU的测量来配准激光点,并用优化来校正IMU的漂移和偏置。此外,他们使用多个双轴激光雷达来绘制一个地下矿井(Zlot和Bosse2012)。该方法包含了一个IMU,并使用循环闭环来创建大型建图。该方法运行速度快。然而,由于该方法依赖于批处理来开发精确的地图,目前很难在在线应用中使用它来提供实时状态估计和建图。
同样的运动分布问题也存在于基于视觉的状态估计中。使用滚动快门相机,图像像素会随着时间的推移而被连续感知,从而导致每个像素读出的时间不同。处理滚动快门效应的最先进的视觉里程计方法受益于IMU(Guo等人2014年、李和Mourikis2014)。该方法使用IMU机理来补偿给定的像素读出时间的运动。在本文中,我们也可以选择使用IMU来抵消非线性运动,并提出方法来求解线性运动。
从特征的角度来看,巴福特等人的方法(董和巴福特2012、安德森和巴福特2013、唐和巴福特2013)从激光强度的返回值来创建视觉图像,并匹配视觉上不同的特征(Bay等人)从而在图像之间恢复运动,这需要具有强度值的密集点云。另一方面,Bosse和Zlot的方法(Bosse和Zlot2009、Bosse等2012、Zlot和Bosse2012)匹配由局部点集群形成的时空小块。与董和巴福特2012、安德森和巴福特2013以及唐和巴福特2013相比,我们的方法对点云密度的要求较少,并且不需要强度值,因为它提取并匹配笛卡尔空间的几何特征。它在边缘和局部平面上使用两种类型的点特征(边缘点,面点),并将它们分别与边缘线段和局部平面小块进行匹配。
用我们提出的方法实时产生的地图与Bosse和Zlot的地图质量上相似。区别在于,我们的方法可以为自动驾驶车辆的引导提供运动估计。该论文是我们会议论文的扩展版本(Zhang和Singh2014)。我们用更多的实验来评估该方法,并提供了更多的细节。
本文所解决的问题是利用三维激光雷达感知的点云进行自我运动估计,并建立一个穿越环境的地图。我们假设激光雷达本质上是用精确已知的激光雷达内部运动学来校准的(内在校准使激光点的三维投影成为可能)。我们还假设激光雷达的角速度和线性速度随时间的变化是平滑和连续的,没有突变。第二个假设将通过使用IMU来发布。
3 Notations and task description
作为本文的一个惯例,我们使用右大写符号来表示坐标系。我们将sweep定义为激光雷达完成一次扫描覆盖。我们使用![]() 表示第k帧点云。雷达坐标系
表示第k帧点云。雷达坐标系![]() 是一个3D坐标系,其原点为雷达的几何中心,这里我们使用相机的惯例,X轴朝左,Y轴朝上,Z轴朝前。使用
是一个3D坐标系,其原点为雷达的几何中心,这里我们使用相机的惯例,X轴朝左,Y轴朝上,Z轴朝前。使用![]() 来表示第k帧点云的第i个点。
来表示第k帧点云的第i个点。![]() 表示第k帧扫描时,在雷达坐标系下,t时刻投影一点相对于k帧初始时刻的位姿变换。世界坐标系
表示第k帧扫描时,在雷达坐标系下,t时刻投影一点相对于k帧初始时刻的位姿变换。世界坐标系![]() 与初始时刻的雷达坐标系
与初始时刻的雷达坐标系![]() 是有关联的。定义第k帧第i个点在世界坐标系下的位置为
是有关联的。定义第k帧第i个点在世界坐标系下的位置为![]() ,记
,记![]() 为t时刻收到的一个点相对世界坐标系的变换。
为t时刻收到的一个点相对世界坐标系的变换。
问题的定义:
给出一个雷达殿宇序列![]() ,计算雷达在世界坐标系中的自我运动,
,计算雷达在世界坐标系中的自我运动,![]() 以及环境地图。
以及环境地图。
算法验证:
本文的研究在四种传感器系统上进行了验证:来回旋转激光系统、连续旋转激光系统、velodyne HDL-32传感器系统和KITTI基准使用的传感器系统。
我们以第一个激光雷达硬件为例来说明该方法,因此我们在本文的前面引入了激光雷达硬件,以帮助读者理解该方法。其余的传感器将在实验部分中介绍。
4 软硬件架构
硬件介绍
上图是一个三维激光雷达在实验评价中的应用实例。我们将使用来自这个传感器的数据来说明该方法。该传感器由一个由用于旋转运动的电机驱动的Hokuyo激光扫描仪和一个测量旋转角度的编码器组成。该激光扫描仪的FOV视场角为180°,角度分辨率为0.25°,即一线是720个点。扫描速率为40线/秒。控制电机从−90°旋转到90°,电机的角速度设置为180°/s,激光扫描仪的水平姿态为零,即Z轴处于水平面,而后电机控制雷达沿着Z轴转动,因此对应一个sweep是电机从−90°旋转到90°(或者反向),持续1s。在这里,请注意,对于一个连续旋转的激光雷达,一个扫描只是一个半球形的或一个全球形的旋转。板载编码器以0.25°角度分辨率测量电机旋转角度,激光点反向投影到激光雷达坐标系。
软件框架
我们将一个sweep的多帧雷达点云,记作![]() (注意:一帧点云代表2D激光雷达一帧数据,以本文所用2D雷达为例,其频率为40Hz,也就是1秒钟获得40帧FOV视野中的点云,而旋转电机是180°/s,当旋转电机扫过一个sweep时花费1s,雷达已经获得了40帧数据,40帧数据合并起来,就是上图的
(注意:一帧点云代表2D激光雷达一帧数据,以本文所用2D雷达为例,其频率为40Hz,也就是1秒钟获得40帧FOV视野中的点云,而旋转电机是180°/s,当旋转电机扫过一个sweep时花费1s,雷达已经获得了40帧数据,40帧数据合并起来,就是上图的![]() )。当第k次sweep时,将
)。当第k次sweep时,将![]() 输入两个算法中。雷达里程计使用的连续两次sweep点云数据,所得到的里程计是用于sweep去畸变的,它的运行频率是10Hz。所输出的结果又用于建图,使用两帧已经去畸变的点云,以1Hz频率进行匹配和配准,建立地图,最后,将两种算法发布的姿态变换进行集成,生成一个关于激光雷达姿态相对于地图的10hz左右的变换输出(为了输出定位的位姿current_pose)。
输入两个算法中。雷达里程计使用的连续两次sweep点云数据,所得到的里程计是用于sweep去畸变的,它的运行频率是10Hz。所输出的结果又用于建图,使用两帧已经去畸变的点云,以1Hz频率进行匹配和配准,建立地图,最后,将两种算法发布的姿态变换进行集成,生成一个关于激光雷达姿态相对于地图的10hz左右的变换输出(为了输出定位的位姿current_pose)。
5 Lidar odometry
5.1 Feature point extraction
我们注意到许多三维激光雷达自然地在![]() 中产生不均匀分布的点。以上图中的激光雷达为例,来自激光扫描仪的返回器在一次扫描内的角度分辨率为0.25°,这些点位于一个扫描平面上。 垂直于扫描平面方向的分辨率为180°/40=4.5°,这个分辨率是什么意思呢,就是2D激光雷达扫描一周时,雷达已经旋转了4.5°。考虑到这一事实,仅使用单个激光扫描帧的信息从
中产生不均匀分布的点。以上图中的激光雷达为例,来自激光扫描仪的返回器在一次扫描内的角度分辨率为0.25°,这些点位于一个扫描平面上。 垂直于扫描平面方向的分辨率为180°/40=4.5°,这个分辨率是什么意思呢,就是2D激光雷达扫描一周时,雷达已经旋转了4.5°。考虑到这一事实,仅使用单个激光扫描帧的信息从![]() 中提取特征点,因为它们具有共面几何关系。
中提取特征点,因为它们具有共面几何关系。
我们选择在尖锐的边缘和平面的表面斑块上的特征点。记i为![]() 中的一个点,记
中的一个点,记![]() 为与i同一个雷达帧的连续不断点云数据。i的两边都有点云,相邻两个点的角度差为角度分辨率0.25°,因此我们使用以下公式计算曲率。这个公式表示标准化了到雷达的距离。这也是为了消除尺度效应才能用于远处和近处的点。
为与i同一个雷达帧的连续不断点云数据。i的两边都有点云,相邻两个点的角度差为角度分辨率0.25°,因此我们使用以下公式计算曲率。这个公式表示标准化了到雷达的距离。这也是为了消除尺度效应才能用于远处和近处的点。
根据c值对一帧雷达数据中的点进行排序,然后选择最大c的点,尖点,即边点,最小c的点,即平面点。为了在环境中均匀地分布特征点,我们将一个扫描分成四个相同的子区域,每个子区域选择最大的2个角点和4个面点。而且设置角点和面点时需要满足阈值,只有c大于或小于0.005时,而且选的点数小于子区域最大点数。
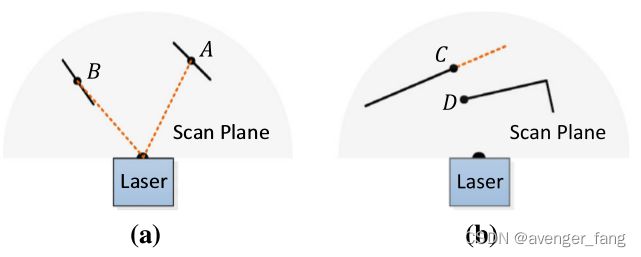
在选择特征点时,我们希望避免周围的点已经被选择过点,或与激光束大致平行的局部平面上的点,这些点通常不可靠。此外,我们希望避免选择遮挡区域边界上的点。
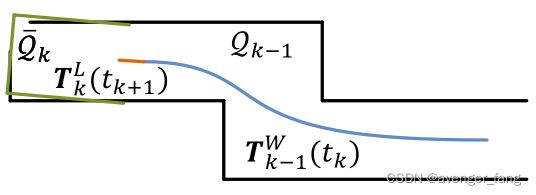
a实线段表示局部表面补丁。点A位于与激光束有一定角度的表面补丁上(橙色虚线段)。B点位于一个与激光束大致平行的表面补丁上。我们把B作为一个不可靠的激光返回,而不选择它作为一个特征点。认为B点不可靠。
b实线段是激光器中可观测到的物体。点C位于被遮挡区域(橙色虚线段)的边界上,可以被检测为边缘点。然而,如果从不同的角度看,遮挡区域会改变并变得可观察。我们不将D作为一个突出的边缘点,也不选择它作为一个特征点(在线颜色图)。不选择D点作为特征点,因为它会改变,离雷达比较近的点不选择。
综上所述,如果选择了一个点,特征点是从最大c值开始的边缘点,以及从最小c值开始的平面点。但有以下三个要求:
- 所选边点或平面点的数量不能超过子区域的最大值;
- 它的周围点都没有被选择;
- 它不能在正常距激光束10°以内的表面片上,也不能在被遮挡区域的边界上。
5.2 Finding feature point correspondence
此雷达里程计算法用于估计一个sweep内的雷达运动。假设![]() 为第k sweep的开始时间。在第k-1个sweep结束时,假设这一个sweep所有感知到的点云为
为第k sweep的开始时间。在第k-1个sweep结束时,假设这一个sweep所有感知到的点云为![]() ,该点云为准备投射到
,该点云为准备投射到![]() 时刻的点云。然后我们记录
时刻的点云。然后我们记录![]() 为该sweep去畸变后的点云,也就是说,
为该sweep去畸变后的点云,也就是说,![]() 将与最新的一个sweep点云
将与最新的一个sweep点云![]() 来估计雷达的运动。我们假设此刻的
来估计雷达的运动。我们假设此刻的![]() 和
和![]() 均为已知的,然后我们开始研究两帧之间的对应关系。对于
均为已知的,然后我们开始研究两帧之间的对应关系。对于![]() ,我们通过上一节完成角点和面点的提取,我们用
,我们通过上一节完成角点和面点的提取,我们用![]() 和
和![]() 来分别表示第k次sweep的角点和面点的集合,我们从
来分别表示第k次sweep的角点和面点的集合,我们从![]() 中找到角点线来对应角点集合
中找到角点线来对应角点集合![]() 中的点,以及
中的点,以及![]() 中的面片作为角点集合
中的面片作为角点集合![]() 的对应点。
的对应点。
在第k sweep的开始,![]() 是空集。随着sweep的进行,点云数量逐渐增多。在此期间雷达里程计能够递归地估计雷达的6D运动姿态,随着点数的增多,参与计算的点也增多,角点集和面点集也都投影到sweep开始时的,我们用
是空集。随着sweep的进行,点云数量逐渐增多。在此期间雷达里程计能够递归地估计雷达的6D运动姿态,随着点数的增多,参与计算的点也增多,角点集和面点集也都投影到sweep开始时的,我们用![]() 和
和![]() 来代表对应投影的点云集合,对于其中
来代表对应投影的点云集合,对于其中![]() 和
和![]() 的点,我们打算在
的点,我们打算在![]() 点云中找到其最邻近的点,这里,我们把在雷达坐标系下
点云中找到其最邻近的点,这里,我们把在雷达坐标系下![]() 的
的![]() 点云以3D KD-tree存储以方便查找。
点云以3D KD-tree存储以方便查找。
上图(a)代表了寻找边(角点)线作为一个角点的对应特征的过程。假设i为角点集合![]() 的一个角点,角点线由两个点表征。假设j为在
的一个角点,角点线由两个点表征。假设j为在![]() 中与i点最近邻的点,l点代表上一帧和随之而来的后续一帧,
中与i点最近邻的点,l点代表上一帧和随之而来的后续一帧,![]() 就形成了对i点的对应。接着需要验证j点和l点均为角点,我们需要根据上面的局部曲率满足c>0.005。在这里,我们特别要求j和l来自不同的扫描线(多线雷达),考虑到单个扫描不能包含来自同一边线的多个点,只有一个例外,那就是当边线在扫描平面上时。但是,如果是这样,则边线就会退化,在扫描平面上呈直线出现,首先不应该提取边缘线上的特征点。
就形成了对i点的对应。接着需要验证j点和l点均为角点,我们需要根据上面的局部曲率满足c>0.005。在这里,我们特别要求j和l来自不同的扫描线(多线雷达),考虑到单个扫描不能包含来自同一边线的多个点,只有一个例外,那就是当边线在扫描平面上时。但是,如果是这样,则边线就会退化,在扫描平面上呈直线出现,首先不应该提取边缘线上的特征点。
上图(b)代表了 寻找面特征所对应面片特征的过程。假设 i为面点集合![]() 中的一个点,小平面片由三个点进行表征。与上一段类似,我们找到j为在
中的一个点,小平面片由三个点进行表征。与上一段类似,我们找到j为在![]() 中与i点最近邻的点,接着我们再找另外两个点m和l,作为i的最近点,一个点与j为同一根扫描线,但又不是j,另一个点为与j上下相邻的扫描线最近点。 这就保证了这三点是非共线的。为了验证j、l和m都是平面点,我们再次检查了局部曲面的平滑性并要求曲率c<0.005。
中与i点最近邻的点,接着我们再找另外两个点m和l,作为i的最近点,一个点与j为同一根扫描线,但又不是j,另一个点为与j上下相邻的扫描线最近点。 这就保证了这三点是非共线的。为了验证j、l和m都是平面点,我们再次检查了局部曲面的平滑性并要求曲率c<0.005。
通过所找到的特征点的对应关系,现在我们推导出表达式来计算一个点距离其特征的距离。在下一节中,我们将通过最小化特征点的总距离来恢复激光雷达的运动。我们从边点开始。
所有的坐标都是在雷达坐标系![]()
5.3 Motion estimation
假设激光雷达的运动模型与恒定的角速度和线性速度在一个sweep。这允许我们在不同时间接收的点姿态变换能够进行线性插值。设![]() 为当前时间,
为当前时间,![]() 为当前sweep开始的时间,
为当前sweep开始的时间,![]() 为雷达的位姿变换从
为雷达的位姿变换从![]() ,
,![]() 包含雷达的6-DOF的位姿,
包含雷达的6-DOF的位姿,![]() ,其中
,其中![]() 表示平移,
表示平移,![]() 表示旋转,他们的坐标系是基于雷达坐标系
表示旋转,他们的坐标系是基于雷达坐标系![]() 的。若给出
的。若给出![]() ,其对应的旋转矩阵能够通过罗德里格斯公式得到:
,其对应的旋转矩阵能够通过罗德里格斯公式得到:
这里的![]() 就是
就是![]() 的反对称阵。
的反对称阵。
给定一个点![]() ,
,![]() ,为第k帧点云中的一个点,设这个点的时间戳为
,为第k帧点云中的一个点,设这个点的时间戳为![]() ,并且令
,并且令![]() 为
为![]() 时间变化内的
时间变化内的
位姿变换,那么![]() 的值就能够通过线性插值进行计算:
的值就能够通过线性插值进行计算:
在这里,要注意的是![]() 是随时间变化的的变量,而且插值使用了当前时间t。回顾
是随时间变化的的变量,而且插值使用了当前时间t。回顾![]() 和
和![]() 是从
是从![]() 点云中提取的角点和面点。下面的公式就是将这些过程中的点投影至该sweep开始时间的过程:
点云中提取的角点和面点。下面的公式就是将这些过程中的点投影至该sweep开始时间的过程:
这里![]() 为角点
为角点![]() 和面点集合
和面点集合![]() 中的一个点,
中的一个点,![]() 就是将点投影至
就是将点投影至![]() 和
和![]() 上的点坐标。回顾角点到边线的距离,面点到面的距离,我们能够得到角点到边线的几何关系,
上的点坐标。回顾角点到边线的距离,面点到面的距离,我们能够得到角点到边线的几何关系,
类似的,我们能够得到面点的关系
最后,我们用LM方法求解雷达运动模型,由上式两个方程,我们归纳为一个非线性方程
这里,![]() 的每一行代表一个特征点,同样对应d的每一行代表一个特征点的距离值。我们计算
的每一行代表一个特征点,同样对应d的每一行代表一个特征点的距离值。我们计算![]() 相对
相对![]() 的雅可比矩阵记作
的雅可比矩阵记作![]() ,接着,我们能够非线性迭代求解方式来最小化d使其接近0。
,接着,我们能够非线性迭代求解方式来最小化d使其接近0。
其中![]() 为LM所确定的因子。
为LM所确定的因子。
5.4 Lidar odometry algorithm
算法过程是:输入为上个sweep的点云![]() ,以及当前帧持续在增加的点云
,以及当前帧持续在增加的点云![]() ,从最后一个递归得到的姿态变换矩阵
,从最后一个递归得到的姿态变换矩阵![]() 作为初始估计值。如果一个新sweep开始,那么就把它
作为初始估计值。如果一个新sweep开始,那么就把它![]() 重新设置为0再开始。接着算法就会提取
重新设置为0再开始。接着算法就会提取![]() 中的角点和面点,对于每一个特征点,找到在
中的角点和面点,对于每一个特征点,找到在![]() 的对应点。
的对应点。
该算法为每个特征点分配一个双分权值,如下式所示。距离较大的特征点对应项的赋值较小,将距离大于阈值的特征点视为异常值,赋值为零。
上述的r为对应的最小二乘法的残差,![]() 是残差与中位数的绝对偏差,h为矩阵
是残差与中位数的绝对偏差,h为矩阵![]() 对角线上对应的元素
对角线上对应的元素
接着,更新一次迭代。如果找到收敛性,或满足最大迭代次数,则非线性优化终止。如果算法到达sweep结束,![]() 被投影到使用扫描期间估计运动的
被投影到使用扫描期间估计运动的![]() 时间戳,形成了
时间戳,形成了![]() 。这为下一次sweep做好了准备与
。这为下一次sweep做好了准备与![]() 进行。对于下一轮的递归,算法只返回变换
进行。对于下一轮的递归,算法只返回变换![]() 。
。
6 Lidar mapping
建图算法的运行频率比测程算法的运行频率低,每次sweep只调用一次。在第k sweep结束,雷达里程计产生一个去畸变的点云![]() ,及同时的位姿变换
,及同时的位姿变换![]() ,包含从
,包含从![]() 在扫描sweep过程中的激光雷达运动,然后建图算法在世界坐标系中配准
在扫描sweep过程中的激光雷达运动,然后建图算法在世界坐标系中配准![]() 。为了展现这一过程,我们定义
。为了展现这一过程,我们定义![]() 为地图上的点云,累计到k-1 sweep,记
为地图上的点云,累计到k-1 sweep,记![]() 为雷达在地图上的位姿,这是是第k-1 sweep结束后的
为雷达在地图上的位姿,这是是第k-1 sweep结束后的![]() 时刻的。随着雷达里程计输出,建图算法能够扩展
时刻的。随着雷达里程计输出,建图算法能够扩展![]() 从
从![]() 到
到![]() ,为了能够获得
,为了能够获得![]() ,并且加去畸变之后的点云
,并且加去畸变之后的点云![]() 转换到世界坐标系下形成点云
转换到世界坐标系下形成点云![]() 。接着算法通过将两个地图
。接着算法通过将两个地图![]() 和
和![]() 进行优化得到准确的雷达位姿
进行优化得到准确的雷达位姿![]() 。
。
特征点的提取方法与第二节相同。5.1,但使用了10次的特征点。为了找到特征点的对应关系,我们将点云存储在地图上![]() ,在10m的范围内的地图,local map。这些点都使用3D kdtree进行存储与特征提取。然后我们寻找距离
,在10m的范围内的地图,local map。这些点都使用3D kdtree进行存储与特征提取。然后我们寻找距离![]() 中的特征点10cmX10cmX10cm的特定区域。我们假定
中的特征点10cmX10cmX10cm的特定区域。我们假定![]() 为周围点集合。对于一个边(角)点,我们只保留周围邻近点
为周围点集合。对于一个边(角)点,我们只保留周围邻近点![]() 中边线上的点,同样对于平面点,我们也只保留其周围点的平面点。这些点根据曲率c值进行区分,此处我们使用阈值0.005进行区分。接下来,我们计算
中边线上的点,同样对于平面点,我们也只保留其周围点的平面点。这些点根据曲率c值进行区分,此处我们使用阈值0.005进行区分。接下来,我们计算![]() 的协方差矩阵,这里记作
的协方差矩阵,这里记作![]() ,获取协方差矩阵的特征值和特征向量,分别记作
,获取协方差矩阵的特征值和特征向量,分别记作![]() 和
和![]() 。这些值决定了点簇的姿态,从而决定了点到线和点到平面的距离。特别地,如果
。这些值决定了点簇的姿态,从而决定了点到线和点到平面的距离。特别地,如果![]() 邻近点分布于一条边线上,
邻近点分布于一条边线上,![]() 就包含了一个特征值会明显大于其他两个,且最大特征值所对应的特征向量就代表了边线的方位;另一方面,若
就包含了一个特征值会明显大于其他两个,且最大特征值所对应的特征向量就代表了边线的方位;另一方面,若![]() 邻近点分布在一个平面上,那么
邻近点分布在一个平面上,那么![]() 就包含了两个大的特征值,有一个比它们两个明显小的得多的特征值,那个小得多的特征值所代表的特征向量就表征着平面的法线方向。已知边线或者平面的方位,其位置我们假设其穿过
就包含了两个大的特征值,有一个比它们两个明显小的得多的特征值,那个小得多的特征值所代表的特征向量就表征着平面的法线方向。已知边线或者平面的方位,其位置我们假设其穿过![]() 的质心。
的质心。
为了计算从一个特征点到其对应关系的距离,我们在一条边线上选择两个点,在一个平面补丁上选择三个点。这允许使用与(2)和(3)相同的公式来计算距离。然后,推导出每个特征点作为(7)或(8)的方程,但不同的是在点云![]() 中,所有点都使用同一时间戳
中,所有点都使用同一时间戳![]() ,采用适应于鲁棒拟合(Andersen 2008)的莱文伯格马夸特方法(哈特利和齐瑟曼2004)再次求解,接着进行点云配准,将
,采用适应于鲁棒拟合(Andersen 2008)的莱文伯格马夸特方法(哈特利和齐瑟曼2004)再次求解,接着进行点云配准,将![]() 点云配准到地图中。
点云配准到地图中。
为了均匀地分布这些点,每次新的扫描与地图合并时,都通过体素网格过滤器(Rusu和Coussins2011)缩小地图云。体素-网格过滤器平均每个体素中的所有点云,在体素中留下一个平均点。边缘点和平面点使用不同的体素大小。有边缘点,体素大小为5厘米×5厘米×5厘米。平面点10cm×10cm×10cm。该地图被截断在传感器周围的500米×500米×500米的区域,以限制内存的使用。
位姿变换的积分如下图所示。蓝色区域表示激光雷达建图的姿态输出![]() ,每次sweep都会生成一次。橘色的区域表示来自雷达里程计的位姿输出
,每次sweep都会生成一次。橘色的区域表示来自雷达里程计的位姿输出![]() ,其频率为10Hz。那么雷达相对于地图的位姿就是这两个位姿变换的结合,也就是说雷达相对于地图的位姿频率与雷达里程计的频率都是10Hz。
,其频率为10Hz。那么雷达相对于地图的位姿就是这两个位姿变换的结合,也就是说雷达相对于地图的位姿频率与雷达里程计的频率都是10Hz。
7 Experiments
在实验中,处理激光雷达数据的算法运行在2.5GHz四核和6Gib内存的笔记本电脑上,在Linux的机器人操作系统(ROS)上实现。该方法总共消耗了两个线程,里程计程序和建图程序运行在两个独立的线程上。
7.1 Accuracy tests
该方法已经在图2中的系统使用激光雷达在室内和室外环境中进行了测试。在室内测试中,激光雷达与电池和笔记本电脑一起放在一辆手推车上,一个人推着手推车走着。图10a,c显示了在两个具有代表性的室内环境中构建的地图,一个窄长走廊和一个空旷的大厅。图10b,d显示了从同一场景中拍摄的两张照片。在户外测试中,激光雷达被安装在地面行走车辆的前部。在图10e,g中显示了由两排树木之间的植被道路和果园生成的地图,照片分别见图10f,h。在所有的测试中,激光雷达以0.5m/s的速度移动。
为了评估地图的局部精度,我们从相同的环境中收集了第二组激光雷达点云。在数据选择过程中,激光雷达保持静止,并放置在每个环境的几个不同的位置。这两个点云采用点到平面的ICP方法进行匹配和比较(精度对比通过建立的地图和静止采集的雷达点云对比)。匹配完成后,将一个点云与第二个点云中相对应的平面小块之间的距离视为匹配误差。图11显示了误差分布的密度。这表明室内环境中的匹配误差比室外环境中的要小。因为在自然环境中的特征匹配不如在人造结构化环境中的精确。
此外,我们想了解激光雷达里程计和激光雷达建图的功能效果,并得到最终的精度。为此,我们取图1中的数据集,并显示每个算法的输出。该轨迹的长度为32米。图12a使用激光雷达里程计的输出直接配准激光点云,而图12b是通过激光雷达建图优化的最终输出。正如我们在开始提到的,激光雷达里程计的作用是估计传感器的速度和消除传感器的点云运动畸变。激光雷达里程计的低保真度不能保证准确的建图。另一方面,激光雷达建图的进一步仔细的扫描配准,以保证在地图上的准确性。表1显示了两个程序在精度测试中的计算时间消耗。我们看到激光雷达建图总共需要6.4倍的激光雷达里程计的计算来消除漂移。在这里,请注意,激光雷达里程计被调用10次,而激光雷达建图仅被调用一次,这导致两个线程上的计算负荷在相同的水平上。
此外,我们还进行了测试来测量运动估计值的累积漂移。我们选择走廊来进行含有一个闭环的室内实验,这让我们可以在同一个地方开始和结束。运动估计在起始位置和结束位置之间产生一个间隙,这个间隙就表明了一个回环的漂移量。
对于室外实验,我们选择果园环境。携带激光雷达的地面车辆配备了高精度GPS/INS,用于地面真实信息采集。将测量到的漂移与行走的距离作为相对精度进行比较,列于表2中。具体来说,Test1使用了与图10a、g相同的数据集。一般来说,室内试验的相对精度约为1%,室外试验约为2.5%。
7.2 Tests with IMU assistance
我们将一个Xsens MTi-10 IMU安装到到激光雷达上,以处理快速的速度变化。点云在发送到本文提出的算法之前,通过两种方式进行了预处理。(1)从IMU的方向上,在一次sweep中接收到的点云时进行了旋转操作,以使得与当前sweep的激光雷达的初始方向对齐,(2)使用加速度测量,运动畸变被部分消除,就像激光雷达在sweep过程中以恒定的速度移动一样。在这里,IMU的方向是通过一个卡尔曼滤波器将陀螺仪的角速率和加速度计的读数积分得到的。经过IMU预处理后,所要求解的运动是来自IMU的姿态漂移,假设在一个sweep范围内速度为线性的。因此,它满足了激光雷达在一个sweep范围内具有线性运动的假设。然后通过激光雷达里程计和建图程序对点云进行处理。
图13
图13a显示了一个示例结果。一个人拿着激光雷达,走在楼梯上。在计算红色曲线时,我们使用IMU提供的方向,而我们的方法只估计平移。在5分钟的数据收集过程中,方向漂移超过25°。绿色曲线只依赖于我们的方法中的优化,假设IMU不可用。蓝色曲线使用IMU数据进行预处理,然后采用所提出的方法。我们观察到绿色和蓝色的曲线之间有微小的差异。图13b为与蓝色曲线对应的地图。在图13c中,我们比较了图13b中黄色矩形中的地图的两个封闭视图。上、下图分别对应蓝色曲线和绿色曲线。仔细的比较可以发现,上图的边缘比下图的边缘更清晰(蓝色的更清晰,使用了IMU的建图更清晰)。
表3比较了使用和不使用IMU的运动估计的相对误差。激光雷达是由一个人以0.5m/s的速度行走,并以0.5米左右的大小上下移动激光雷达。地面真值是用卷尺手动测量的。在所有四个测试中,在IMU的协助下使用本文所提出的方法获得最高的精度,而使用IMU的方向只能导致最低的精度。结果表明,该方法可以有效地抵消非线性运动,该方法可以处理线性运动。
7.3 Tests with micro-helicopter datasets
我们进一步利用一个八旋翼微型飞无人机中收集的数据来评估本文提出的算法。如图14所示,直升机安装了一个2轴激光雷达,除激光扫描仪外,它与图2中的激光雷达的设计相同持续旋转。对于这样的激光雷达单元,sweep被定义为在慢轴上的半球形旋转,持续1s钟。一个微应变Microstrain 3DM-GX3-45 IMU也被安装在直升机上。里程计和建图程序处理激光雷达和IMU数据。
我们在图中显示了来自两个数据集的结果。图15和图16。在这两个测试中,直升机都是以1m/s的速度手动飞行的。在图15中,直升机从桥的一侧开始,从桥下飞行,然后第二次返回到桥下飞行。在图16中,直升机从从地面起飞开始,以返回地面着陆结束。在图15a和16a中,我们显示了飞行的轨迹,并在图15b和16b中,我们展示了放大的地图视图,放大区域对应于图15c和16c中黄色矩形内的区域。我们无法获得直升机姿态或地图的地面真值。对于两个测试中相对较小的环境,该方法不断地对测试开始时构建的地图进行重新定位。因此,计算循环闭合误差变得毫无意义。相反,我们只能直观地检查放大视图中的地图的准确性(还没能找到更佳的方法定量评价建图精度)。
7.4 Tests with a Velodyne lidar
这些实验使用了安装在图17所示的两台车辆上的 Velodyne HDL-32E激光雷达。图17a是一个在人行道和越野地形上行驶的多功能车辆。图17b是一辆在街道上行驶的乘用车。对于两种车辆,激光雷达都安装在顶部,以避免覆盖范围可能被车身遮挡。Velodyne HDL-32E是一种单轴激光扫描仪。它将32束激光束同时投射到三维环境中。我们把每一个由激光束形成的平面都当作一个扫描平面。一个sweep被定义为激光扫描仪的一圈旋转。激光雷达默认可以获得10hz的扫描结果。我们配置激光雷达里程计运行在10Hz来处理单个scan。雷达建图堆栈会扫描一秒钟来进行批处理优化。两个程序的计算消耗如表4所示。
图18显示了大学校园的的结果。数据与图17a中的车辆一起记录了1.0km的行走。测试期间的行驶速度保持在2-3m/s。图18a显示了最终构建的地图。图18b显示了估计的轨迹(红色曲线)和覆盖在卫星图像上的配准激光点。通过将运动轨迹与人行道相匹配(车辆不在街道上行驶),并且激光指向建筑的墙壁,我们确定水平位置漂移为≤1m。通过比较两侧的建筑,我们能够确定垂直漂移为≤1.5m。这导致总的位置误差占旅行距离为≤0.2%。
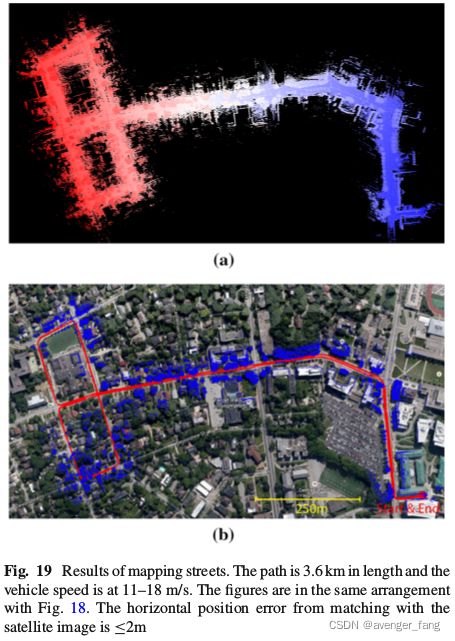
图19显示了来自另一个测试的结果。我们驾驶图17b中的车辆在街道上行驶了3.6公里。除等待红绿灯外,车速大多在11-18m/s之间。图19中的图形的组织方式与图18相同。通过与卫星图像的比较,我们确定了水平位置误差为≤2m。然而,对于垂直精度,我们无法进行评估。
7.5 Tests with KITTI datasets
最后,我们使用KITTI里程计基准测试了本文的方法(Geigeretal.2012,2013)。在道路驾驶场景中,这些数据集是由安装在乘用车顶部的传感器进行记录的。
如图20所示,该车辆配备有彩色立体相机,单色立体相机,一个HDL-64E激光扫描仪,和高精度GPS/INS地面真值。激光数据以10Hz记录,并被用于运动估计的方法。为了达到最大的精度,扫描数据的处理方式与部分略有不同7.4节(上一节)。激光雷达建图不是从激光雷达里程计中叠加10次scan,而是以与激光雷达里程计相同的频率运行,并处理每个单独的扫描。这导致系统以实时速度的10%运行,需要一秒钟来处理一次scan。
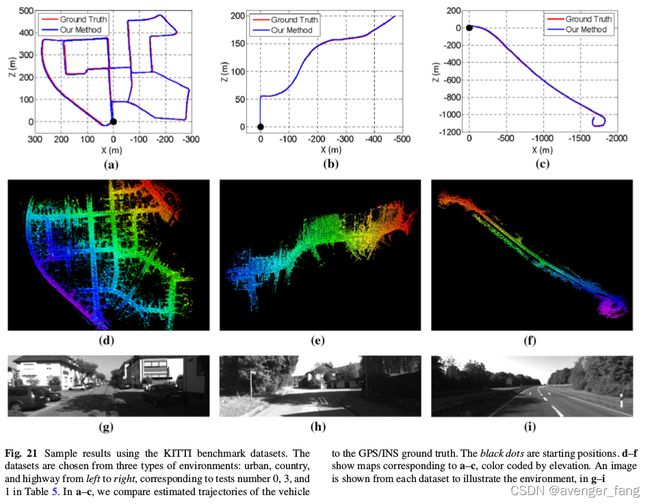
数据集包含11个测试,提供GPS/INS地面真值。数据集中的最大驱动速度达到85km/h(23.6m/s)。数据主要涵盖三种类型的环境:周围有建筑的“城市”、现场有植被的小道路上的“乡村”和道路较宽、车速较快的“高速公路”。图21显示了来自这三个环境的示例结果。在最上面一行,我们显示了与GPS/INS地面真值相比的估计轨迹。在中间和底部行,显示每个数据集的地图和相应的图像。这些地图是按海拔高度用颜色编码的。1.数据集的完整测试结果。图21中从左到右的三个测试分别是表中的数据集0、3和1。在这里,精度是通过基于三维坐标,使用100,200,...,800米长的分割轨迹来计算平均相对位置误差的。
我们的结果精度在KITTI里程计基准上排名第二,无论感知传感器的型号,与移动距离相比,结果的平均位置误差为0.88%。研究结果优于最先进的基于视觉的方法(立体视觉里程计法)(Persson et al. 2015; Badino and Kanade 2011, 2013; Lu et al. 2013; Bellavia et al. 2013年的那个方法的位置误差超过14%,方向误差超过24%。事实上,该方法也部分被排名第一的方法使用,该方法运行视觉里程计的运动估计和所提出的运动提纯方法(Zhang和Singh2015 VLOAM)。我们认为基于激光的状态估计优于基于视觉的方法,因为激光雷达具有测量远处点的能力。激光雷达的范围误差是相对恒定的,其测量的距离和远离车辆的点保证了扫描匹配时的方向精度。
8 Discussion
在构建复杂系统时,一个问题是系统中的哪些组件能作为确保性能的关键。我们的第一个答案是双层数据处理结构。这允许我们将状态估计问题分解为两个更容易解决的问题。激光雷达里程计只关心传感器的速度和运动畸变去除。由激光雷达里程计得出的速度估计并不精确(见图12a),但足以分解点云。 之后建图模块只需要考虑刚体变换即可进行精确的扫描匹配。
我们实现几何特征检测和匹配是实现在线和实时处理的一种手段。特别是在激光雷达里程计中,匹配不必非常精确,但高频对于点云解耦更为重要。该实现以处理速度为其优先级。然而,如果有足够的计算量可用,例如使用GPU加速,那么实现就不那么必要了。我们确实可以选择选择激光雷达里程计和激光雷达建图之间的频率比。将比值设置为10是我们的偏好(激光雷达建图比激光雷达里程计慢一个数量级)。这意味着激光雷达建图堆栈从10次scan激光雷达里程计中输出一次批优化。若设置该比率(10)更高通常会导致更大的漂移。
此外,每次激光雷达建图完成处理时,一个跳跃将被引入到运动估计。这个比率能够保持运动估计的平稳性。另一方面,将比率设置为较低将会导致更多的计算,而且通常是不必要的。该比率还平衡了两个CPU线程上的计算负载。更改比率将使一个线程比另一个线程有更多的计算负荷。
9 Conclusion and future work
利用旋转激光扫描仪上的点云进行运动估计和建图可能是困难的,因为该问题涉及到激光雷达云中的运动恢复和运动畸变的校正。本文提出的方法通过两种并行运行的算法来划分并解决该问题。通过两种算法的协同作用,可以实时实现精确的运动估计和映射。该方法已经在涵盖不同类型环境的大量实验中进行了测试,使用了作者收集的数据以及来自KITTI里程计基准的数据集。由于目前的方法不能识别环路闭合,我们未来的工作涉及开发一种方法,通过闭合环路来纠正运动估计漂移。