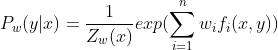《机器学习方法（第三版）—— 李航》学习笔记（四）

目录

第六章 逻辑斯谛回归与最大熵模型

第九章 EM算法及其推广

第十章 隐马尔可夫模型

第十一章 条件随机场

---

提示：监督学习后几章概念性和推理较多，就不大量抄概念了。。。

第六章 逻辑斯谛回归与最大熵模型

1、逻辑斯谛回归模型是由以下条件概率分布表示的分类模型，可以用于二类或多类分类。

这里，x为输入特征，w为特征权值。

逻辑斯蒂回归模型源自逻辑斯谛分布，其分布函数F(x)是S形函数。逻辑斯谛回归模型是由输入的线性函数表示的输出的对数几率模型。

2、最大熵模型是由以下条件概率分布表示的分类模型，也可以用于二类或多类分类。

其中，Zw(x)是规范化因子，fi为特征函数，wi为特征的权值。

3、最大熵模型可以由最大熵原理推导得出。最大熵原理是概率模型学习或估计的一个准则。最大熵原理认为在所有可能的概率模型（分布）的集合中，熵最大的模型是最好的模型。

最大熵原理应用到分类模型的学习中，有以下约束最优化问题：

min       

求解此最优化问题的对偶问题得到最大熵模型。

4、逻辑斯谛回归模型与最大熵模型都属于对数线性模型。

5、逻辑斯谛回归模型及最大熵模型学习一般采用极大似然估计或正则化的极大似然估计。逻辑斯谛回归模型及最大熵模型学习可以形式化为无约束最优化问题，求解该最优化问题的算法有改进的迭代尺度法，梯度下降法，拟牛顿法。

第九章 EM算法及其推广

1、EM算法是含有隐变量的概率模型极大似然估计或极大后验概率估计的迭代算法。含有隐变量的概率模型的数据表示为P(Y,Z|θ)。这里，Y是观测变量的数据，Z是隐变量的数据，θ是模型参数。EM算法通过迭代求解观测数据的对数似然函数L(θ)=logP(Y|θ)的极大化，实现极大似然估计。每次迭代包括两步：E步，求期望，即求logP(Y,Z|θ)关于P(Z|Y,θ)的期望：

称为Q函数。M步，求极大值，即极大化Q函数得到的参数的新估计值：

在构建具体的EM算法时，重要的时定义Q函数。每次迭代中，EM算法通过极大化Q函数来增大对数似然估计函数L(θ)。

2、EM算法在每次迭代后均提高观测数据的似然函数值，即

在一般条件下EM算法是收敛的，但不能保证收敛到全局最优。

3、EM算法应用极其广泛，主要应用于含有隐变量的概率模型的学习。高斯混合模型的参数估计是EM算法的一个重要应用。

4、EM算法还可以解释为F函数的极大-极大算法。EM算法有许多变形，如GEM算法。GEM算法的特点是每次迭代增加F函数值（并不一定是极大化F函数），从而增加似然函数值。

第十章 隐马尔可夫模型

1、隐马尔可夫模型是关于时序的概率模型，描述由一个隐藏的马尔可夫链随机生成不可观测的状态的序列，再由各个状态随机生成一个观测从而产生观测序列的过程。

隐马尔可夫模型由初始状态概率向量、状态转移概率矩阵A和观测概率矩阵B决定。因此，隐马尔可夫模型可以写成 。

隐马尔可夫模型是一个生成模型，表示状态序列和观测序列的联合分布，但是状态序列预测其对应的标记序列。

2、概率计算问题。给定模型和观测序列，计算模型λ下观测序列O出现的概率P(O|λ)。前向-后向算法通过递推地计算前向-后向概率可以高效地进行隐马尔可夫模型的概率计算。

3、学习问题。已知观测模型，估计模型参数，使得在该模型下观测序列概率P(O|λ)最大。即用极大似然估计的方法估计参数Baum-Welch算法，也就是EM算法可以高效地对隐马尔可夫模型进行训练。它是一种无监督学习算法。

4、预测问题。已知模型和观测序列，求给定观测序列条件概率P(I|O)最大状态序列。维特比算法应用动态规划高效地求解最优路径，即概率最大的状态序列。

第十一章 条件随机场

1、概率无向图模型是由无向图表示的联合概率分布。无向图上的结点之间的连接关系表示了联合分布的随机变量集合之间的条件独立性，即马尔科夫性。因此，概率无向图模型也称为马尔可夫随机场。概率无向图模型或马尔可夫随机场的联合概率分布可以分解为无向图最大团上的正值函数的乘积的形式。

2、条件随机场是给定输入随机变量X条件下，输出随机变量Y的条件概率分布模型，其形式为参数化的对数线性模型。条件随机场的最大特点是假设输出变量之间的联合概率分布构成概率无向图模型，即马尔可夫随机场。条件随机场是判别模型。

3、线性链条件随机场是定义在观测序列与标记序列上的条件随机场。线性链条件随机场一般表为给定观测序列条件下的标记序列的条件概率分布，由参数化的对数线性模型表示。模型包含特征及相应的权值，特征是定义在线性链的边与结点上的。线性链条件随机场模型的参数形式是最基本的形式，其他形式是其简化与变形，参数形式的数学表达式是：

其中，

4、线性链条件随机场的概率计算通常利用前向-后向算法。

5、条件随机场的学习方法通常是极大似然估计方法或正则化的极大似然估计，即在给定训练数据下，通过极大化训练数据的对数似然函数函数估计模型参数。具体的算法有改进的迭代尺度算法、梯度下降法、拟牛顿法等。

6、线性链条件随机场的一个重要应用是标注。维特比算法是给定观测序列求条件概率最大的标记序列的方法。