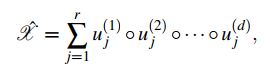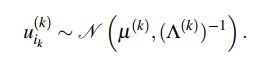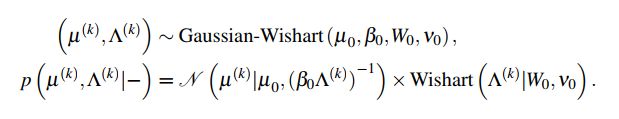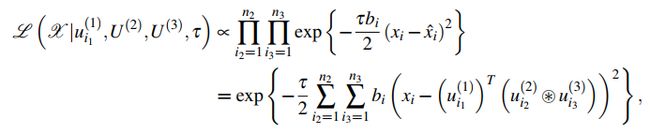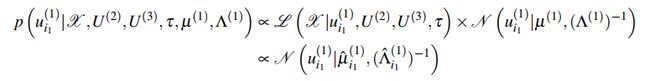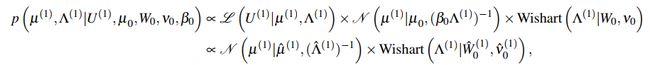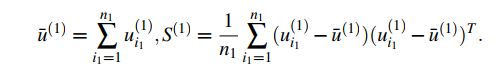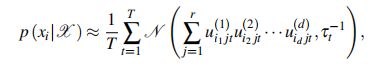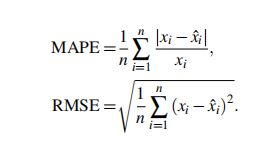张量（五）：张量学习——BGCP
接下来的文章将主要介绍张量在交通领域的实际应用，包括预测、补全等问题。与其他模型相结合，针对具体问题，构建的一系列模型，我这里统称为“张量学习模型”。本文主要介绍Bayesian Gaussian CANDECOMP/PARAFAC tensor decomposition model（BGCP）。源论文请参考《A Bayesian Tensor Decomposition Approach for Spatiotemporal Traffic Data Imputation》
1 背景
随着智能交通系统的发展和应用，大量城市交通数据通过各种来源如环路检测器、摄像机等被捕获，这些数据可用于交通运营和管理应用，包括路由、信号控制、出行时间预测等。通常，我们可以将时空交通数据组织成一个多维结构，即张量。例如监测的一周的交通流数据，每天12个时刻，共监测30个路段，则可构成30*12*7的张量（road segment-day-time of day）。
影响这种时空数据使用的常见缺陷就是缺失问题，导致的因素包括硬件/软件故障、网络通信问题等。缺失的数据很可能是路线规划和旅行时间预测任务等的问题的重要输入。因此，需对缺失数据进行补全。我们将这一类问题称之为tensor imputation。
目前，imputation的算法主要有三大类：预测（prediction）、插值（interpolation）、基于统计学习的方法。
在对时空交通数据进行建模时，必须考虑强时空相关性模式。张量分解是一种捕获多维结构相关性的标准技术。总体思想是使用一个紧凑的结构来建模原始的多维数据，例如CP分解和Tucker分解。对于imputation的任务，我们感兴趣的是缺失值进行强鲁棒性的预测，而不是估计模型参数。这激发了学者们利用概率方法去解决缺失数据的补全问题。
张量中处理缺失值补全的方法主要有两种：
- 使用无分解结构的低秩张量补全方法，这种方法可有效避免非凸优化问题。
- 张量分解，可理解为奇异值分解的高阶扩展。
本篇所说的BGCP模型是对贝叶斯矩阵分解模型的高阶扩展，用来学习时空交通数据中的隐藏统计模式。BGCP是一个完全的贝叶斯模型，描述了数据生成过程，因此可有效进行缺失值补全。
2 BGCP
2.1 模型描述
令
表示d阶张量，使用
去表示张量输入值的索引，用
表示张量输入值。则CP分解可表示为：
详细介绍参考我此前的张量系列博客。将CP分解公式按元素表示（单个输入值）可转化为：
其中
表示第k个因子矩阵
的第
行，第
列的值。由于缺失值的存在，张量X是不完整的，我们用
表示观测值（已知值）的索引。
接下来，介绍一下完整的贝叶斯模型数据生成过程。
首先，假设在CP分解近似X的过程中，每个观测值的噪声项都服从独立的高斯分布。
其中，
表示高斯分布，
表示精度，属于全局参数。
为了正确对张量数据建模，对因子矩阵集合和精度设置灵活的先验分布。具体来说就是假设建立在所有因子矩阵中的行向量之上的先验分布被假设为多元高斯分布。
在贝叶斯模型中，我们为超参数
和
设置共轭高斯-威希特分布（Gaussian-Wishart），可增强模型鲁棒性并在使用抽样算法进行模型推断时加速收敛。超参数
和
定义如下：
威希特分布自由度为
，
的尺度矩阵为
，其表达式如下：
其中，
（迹函数）是方阵主对角线上所有元素之和。
基于高斯假设，精度参数
捕捉了数据中的噪声等级。值得注意的是，交通速度数据中，精度对于我们来说是未知的。因此，设置一个灵活的共轭伽马先验去增加模型的鲁棒性：
其中，
和
是形状参数和比率参数。如果一个随机变量服从
，则
。下图是表征上述贝叶斯概率CP分解数据生成过程的总体图形结构。
对于该模型可通过Gibbs采样算法去做模型推断。
2.2 Gibbs采样算法
Gibbs采样算法是一种用于贝叶斯推断的MCMC算法的常用算法。其核心思想是在每轮迭代中顺序更新所有变量。每个变量都是根据所有其他变量的当前值从其分布中采样而来。Gibbs采样的关键是为所有变量定义这样的分布，这些条件分布通常被称为完全条件。
由于我们在BGCP中对参数和超参数使用了共轭先验，因此可以推断出模型的后验分布。以一个三阶张量为例，接下来我们根据马尔科夫覆盖推导出各参数的封闭后验分布。同样的分析也适用于高阶张量结构。
2.2.1 因子矩阵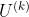采样
因子矩阵采样的目标是去捕捉观测值和超参数，之间的依赖关系。给定一个存在缺失值的张量
,首先定义一个和X相同维度的对照张量B，其输入值1表示观测值，0表示缺失值。
对所有
依次采样来更新因子矩阵
，则每个观测值的噪声项都服从的独立高斯分布可被改为：
其中，
表示哈德马积。
结合上式和前述多元高斯分布表达式可得后验分布，可被写为下述多元高斯分布
其中
同理，参考同样的过程，可写出
和
的后验分布。
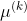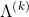2.2.2 和采样
因子矩阵
的似然性可以分解为
个向量的条件分布的乘积：
给定似然性和高斯-维尔特超分布表达式，我们可以写出超参数
和
的联合后验分布并因式分解如下：
两个分布中的参数可被计算如下：
其中
和
是两个统计数字，定义如下：
k=2和k=3时同理。
2.2.3 精度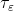采样
所有观测值的似然性如下：
结合上式和的先验分布式可得的后验分布，也是一个由
和
参数化的伽马分布：
其中，
，
。
2.3 实现
BGCP模型的Gibbs采样算法总结如下：
3 实验
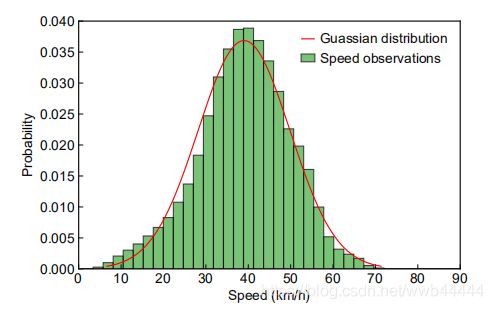
为了验证模型的有效性，基于收集自广州的大量交通速度数据集进行数值实验。数据集生成自一个广泛使用的导航app，数据包括来自214个路段两个月的交通速度观测值。速度数据可被转化为一个三阶张量（路段-日-时间间隔，214*61*144）。其中，大约有1.29%的数据为缺失值。下图为观测速度数据直方图，以及最大似然拟合的高斯分布。如图所示，速度数据被很好的捕获，呈高斯分布，没有任何的极端值。
BGCP补全是通过平稳后的多次Gibbs采样平均化来实现的。
对比实验中，我们将BGCP与high accuracy low-rank tensor completion（HALRTC）和SVD-combined tensor decomposition（STD）作比较。以mean absolute percentage error（MAPE）和root mean square error（RMSE）作为评价指标。
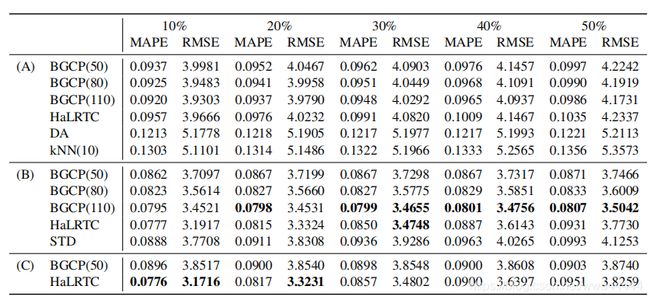
实验结果如下：
10%，20%等代表不同百分比的缺失数量，A，B，C分别代表测试数据为矩阵，三阶张量和四阶张量。相比之下，BGCP表现的补全效果相比于其他对比算法更好，且在三阶张量中表现的最好。
上图为预测结果与真实结果的对比图，可见二者基本吻合，说明BGCP预测效果较好。