tensorflow1.x学习笔记一：基础

---

前言

2022了还学习tensorflow1.x肯定比较奇怪吧，但由于最近需要读懂一个比较旧的tensorflow的代码，必须简单学习一下tensorflow1.x，这篇文件简单记录一下学习过程中用到的实例。

---

一、点乘运算

• 在神经网络中，每一层的计算实际上就是上一层的结果与这一层的权重进行点乘运算。

下面是一个简单的实现了点乘运算的例子：

# coding:utf-8
import tensorflow as tf

x = tf.constant([[1.0, 2.0]])  # 这是一个1*2的定值张量
w = tf.constant([[3.0], [4.0]])  # 这是一个2*1的定值张量
y = tf.matmul(x,w)  # 点乘运算
print(y)  # 输出y是一个1*1的float32类型的张量
with tf.Session() as sess:  # 会话
    print(sess.run(y))  # 输出y的结果

运行结果：

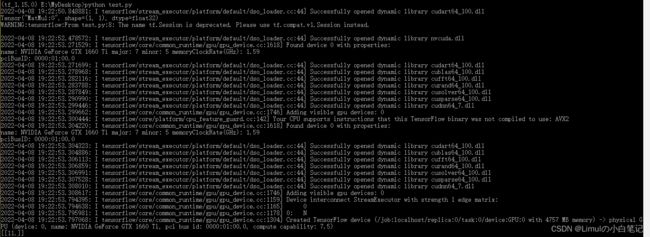
（请忽略中间一大串的提示，那些是使用gpu版本的tensorflow成功打开一些dll动态库的提示）

• 在tensorflow中，需要先定义网络的结构，然后在会话中计算结果。

二、向前运算

• 在神经网络中，权重是我们需要训练得到的参数，所以权重是变量。神经网络在向前传播的过程，就是通过当前权重将所给的输入推理出结果的过程。

下面给出了一个向前传播的例子：

# coding:utf-8
# 两层简单神经网络（全连接）
import tensorflow as tf

# 定义输入和参数
# x = tf.constant([[0.7, 0.5]])  # 这是一个1*2的定值张量
x = tf.placeholder(tf.float32, shape=(None, 2))  # 使用placeholder定义输入，使得可以在sess.run中喂入多组数据，None表示还未知道喂入的输入的组数
w1 = tf.Variable(tf.random_normal([2, 3], stddev=1, seed=1))  # 这是一个以正态分布随机生成的2*3的变量张量，标准差为1，随机种子为1，均值默认为0
w2 = tf.Variable(tf.random_normal([3, 1], stddev=1, seed=1))  # 这是一个以正态分布随机生成的3*1的变量张量，标准差为1，随机种子为1，均值默认为0

# 定义前像传播过程
a = tf.matmul(x, w1)  # a=x*w1(形状1*2的张量与形状2*3的张量相乘得到1*3的张量)
y = tf.matmul(a, w2)  # y=a*w2(形状1*3的张量与形状3*1的张量相乘得到1*1的张量)

# 变量的初始化和运算都要在会话中进行
with tf.Session() as sess:
    # 变量初始化
    init_op = tf.global_variables_initializer()
    sess.run(init_op)

    # 运算并输出结果
    # print("y in test.py is:\n", sess.run(y)
    print("y in test.py is:\n", sess.run(y, feed_dict={x: [[0.7, 0.5], [0.2, 0.3], [0.3, 0.4], [0.4, 0.5]]}))  # 喂入的类型是字典

运行结果（截掉了一大串关于gpu的提示）：

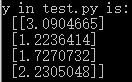
在这个例子中，首先使用tf.placeholder()定义输入，然后将权重定义为变量，然后在会话中将变量初始化，并给出输入进行结果y的推理然后输出结果。

• 在tensorflow中，变量的初始化和结果的计算推理都必须在会话中进行。

三、反向传播

• 神经网络的目的是根据我们所给的输入和理想的输出，在训练中不断更改神经网络中参数，使得输入在经过神经网络向前传播后得到的结果与理想输出尽可能相同。而修改参数就是在反向传播中完成的。
• 如何去描述神经网络的结果与理想输出的差距呢？描述差距的方法有很多，比如平方差等。在神经网络中用来描述神经网络的结果与理想输出的差距的函数叫loss损失函数，这个函数的定义需要在训练神经网络前给出。
• 反向传播时如何更改参数呢？通过计算loss的值，然后以减少loss为目的，去改变参数，常用的方法例如梯度下降法。这个更改参数的方法也需要在训练前给出。

下面这个例子，利用某条规律生成一个模拟的数据集，然后使用神经网络去探索这条规律：

# coding:utf-8
import tensorflow as tf
import numpy as np
BATCH_SIZE = 8  # 一批为8个数据
seed = 23455  # 随机数种子

# 基于seed生成一个随机数生成器，这样通过这个生成器生成的结果可以复现
rng = np.random.RandomState(seed)

# 随机生成X，并根据特定规则得到理想的Y，这个X与Y是用于训练模拟数据集
X = rng.rand(32, 2)  # 根据随机数生成器生成随机的32组，每组2个数字的X数组
Y = [[int(x0 + x1 <1)] for (x0, x1) in X]  # 根据X中每组的两个数x0和x1，满足x0+x1<1则Y中对应那组的数值为1，否则为0，所以Y是个32*1的数组
print("X:\n", X)  # 输出X
print("Y:\n", Y)  # 输出Y

# 定义给神经网络的数据格式
x = tf.placeholder(tf.float32, shape=(None, 2))
y_ = tf.placeholder(tf.float32, shape=(None, 1))  # y_为理想的输出

# 定义参数
w1 = tf.Variable(tf.random_normal([2, 3], stddev=1, seed=1))
w2 = tf.Variable(tf.random_normal([3, 1], stddev=1, seed=1))

# 连接网络
a = tf.matmul(x, w1)
y = tf.matmul(a, w2)  # y为神经网络计算推理的结果

# 定义loss损失函数和反向传播训练方法
loss = tf.reduce_mean(tf.square(y-y_))  # loss为均方误差函数
train_step = tf.train.GradientDescentOptimizer(0.001).minimize(loss)  # 使用梯度下降法降低刚才定义的loss函数，学习率0.001
# train_step = tf.train.MomentumOptimizer(0.001,0.9).minimize(loss)
# train_step = tf.train.AdamOptimizer(0.001).minimize(loss)

# 会话
with tf.Session() as sess:
    # 参数初始化
    init_op = tf.global_variables_initializer()
    sess.run(init_op)

    # 输出训练前的参数初始值
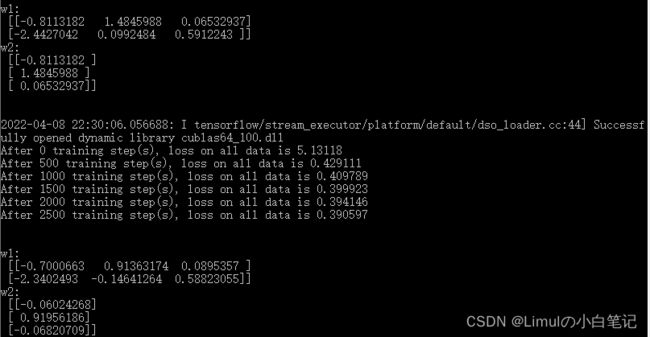
    print("w1:\n", sess.run(w1))
    print("w2:\n", sess.run(w2))
    print("\n")

    # 训练
    STEPS = 3000  # 训练次数
    for i in range(STEPS):
        # 以每批次BATCH_SIZE大小进行训练
        start = (i*BATCH_SIZE) % 32
        end = start + BATCH_SIZE
        sess.run(train_step, feed_dict={x:X[start:end], y_: Y[start:end]})  # 根据反向传播训练方法，喂入模拟数据集进行训练

        # 每500次输出当前的训练结果
        if i%500 == 0:
            total_loss = sess.run(loss, feed_dict={x:X,y_:Y})
            print("After %d training step(s), loss on all data is %g"%(i, total_loss))

    # 输出训练后的参数
    print("\n")
    print("w1:\n", sess.run(w1))
    print("w2:\n", sess.run(w2))

运行结果（前面输出模拟数据集的部分还有一大段关于gpu的提示没有截）：