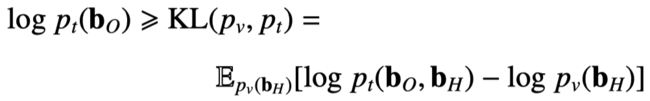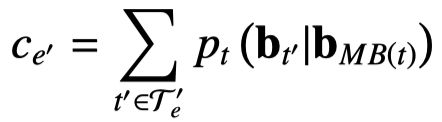论文浅尝 | Explainable Link Prediction in Knowledge Hypergraphs

笔记整理：陈子睿，天津大学硕士

论文链接：https://dl.acm.org/doi/10.1145/3511808.3557316

动机

知识超图链接预测已被认为是各种知识使能下游应用的关键问题。然而，大多数现有方法主要以黑盒方式执行链接预测，它们学习实体关系的低维嵌入进行推理，无法提供人类用户可理解的解释。本文提出了HyperMLN，一个多元、混合、可解释的框架，它用一阶谓词逻辑解释路径推理过程，提供一个知识增强的可解释预测框架，其中逻辑规则中的领域知识用于提升嵌入模型的推理性能，而嵌入空间中的语义信息可以反向优化逻辑规则的权重大小。为给可解释性链接预测方法提供基准规则集，在每个知识超图与知识图谱数据集中挖掘了三种元逻辑规则来解释结果。在实现可解释性的同时，与最先进的知识超图嵌入方法相比，我们的框架在Hits@1指标上平均实现了3.2%的性能提升。

亮点

HyperMLN的亮点主要包括：

（1）探索通过带权重值的逻辑规则构建马尔科夫毯的方式完成对推理结果的解释，包括相关实体及关系对隐藏元组成立的贡献度；

（2）采用数据与知识混合驱动的方式，同时利用向量空间中的语义信息与逻辑规则中的领域知识，完成对隐藏元组的推理。

概念及模型

HyperMLN的关键思想是使马尔科夫逻辑网络适应于多元关系的表示，包括马尔科夫网络中的变量和势函数。接着定义元组的联合分布，通过将知识超图嵌入模型与马尔科夫逻辑网络相结合以完成推理。该组合模型可以通过变分EM算法进行有效训练，其中逻辑规则中编码的领域知识和向量空间中学习的语义信息可以收敛，以提高预测性能。此外，最终的预测结果可以由逻辑规则和相应的马尔可夫毯来解释。

HyperMLN具体由三部分组成：

①基于多元关系的马尔科夫逻辑网络：无需采用star-to-clique转换即可基于逻辑规则将知识超图构建为马尔科夫网络。

②训练与预测：采用变分EM算法同时优化知识超图嵌入模型参数及马尔科夫逻辑网络的逻辑规则权重。

③结果解释：抽取预测元组的马尔科夫毯，基于逻辑规则及权重值解释元组的推理路径。

模型整体框架如图1所示：

图1 模型框架图

（1）基于多元关系的马尔科夫逻辑网络

随着知识超图中关系元数的增长，基于二元关系的马尔科夫逻辑网络在采用star-to-clique分解框架处理知识超图数据时受到了根本性的限制。为此，提出一个基于多元关系的马尔科夫逻辑网络，可直接表示基于多元关系的元组及逻辑规则。该网络使用直接建模的方式表示知识超图，避免分解操作导致的数据冗余及信息丢失，并允许势函数直接使用基于多元谓词构建的规则进行表示。给定一个逻辑规则集，所有元组的联合分布可由以下公式进行定义：

（2）训练与预测

知识超图推理方法通过学习实体和关系在可观测元组中的嵌入来预测隐藏元组。基于这些嵌入，所有元组的联合分布可通过如下公式进行定义：

马尔科夫逻辑网络引入了规则权重，以解决逻辑规则的不确定性。给定一个逻辑规则集合，所有元组的联合分布可定义为：

为了结合马尔科夫逻辑网络和知识超图推理方法，该框架转向优化如下公式所示的对数似然函数下限，因为该下限可被EM算法有效优化：

为了结合马尔科夫逻辑网络和知识超图推理方法，利用如下摊销推理使变分分布与知识超图推理模型参数化，这样，知识超图推理模型所定义的联合分布可以与马尔科夫逻辑网络相结合于变分E步：

该公式通过最小化变分分布和真实分布间的KL散度进行模型优化，隐藏元组的联合分布通过如下方式计算得出：

为学习知识超图推理模型的参数，目标函数被定义为：

(这个公式)

在M步中，为了处理配分函数Z，HyperMLN改为优化伪似然函数，固定知识超图推理模型的参数取值，利用如下公式通过最大化对数似然函数更新逻辑规则的权重：

(这个公式)

（3）结果解释

对每个预测元组而言，在任意逻辑规则中，与预测元组同时出现的元组可在马尔科夫毯中被找到。在马尔科夫毯中出现的所有实体和关系可被合并为集合E'和集合R'，每个实体e'对预测元组为真的置信度可通过如下公式计算：

实验

采用了5个公开数据集进行实验，分别是：JF17K、M-FB15K、FB-AUTO、FB15k和WN18。模型的评价指标为：MRR和Hits@k。

图2 数据集统计数据

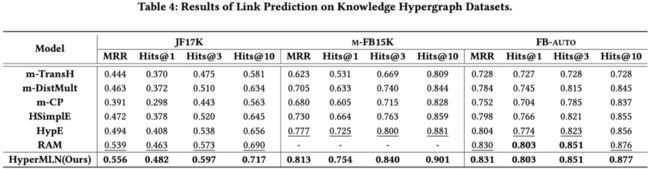
HyperMLN在所有数据集下都优于目前的知识超图推理方法，其性能改进来自于逻辑规则所捕获知识的能力。在知识超图数据集上选择RAM作为所结合的知识超图推理模型。与纯RAM模型及其他知识超图推理方法相比，在所有评价指标上都取得了更好的表现，原因是知识超图推理方法只利用嵌入空间中的语义信息。同时，HyperMLN使用学习到的嵌入来标注马尔科夫逻辑网络发现的隐藏元组，并进一步更新逻辑规则的权重以达到更好的推理性能，这说明了变分 EM 算法可同时对知识超图推理模型的参数和马尔科夫逻辑网络的规则权重进行充分的训练优化，实现逻辑规则中的领域知识与向量空间中的语义信息充分融合，提高知识超图推理模型的预测性能。

图3 知识超图链接预测结果

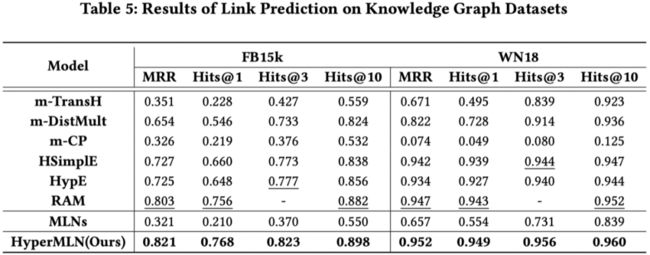
同时，也选择RAM作为知识图谱数据集上的知识超图推理模型。HyperMLN明显优于基于规则的方法，因为HyperMLN使用知识超图推理模型来提升预测性能，与知识超图上的结果类似，将 HyperMLN 应用于知识图谱中同样得到了更好的结果，证明了可解释性链接预测框架 HyperMLN 的有效性。

图4 知识图谱链接预测结果

下图分别显示了用变分EM算法及其变体（仅用变分E步）训练 HyperMLN 的结果。在变分E步中，推理模型从逻辑规则中获得领域知识，而在M步中，逻辑规则的权重值可通过学习的实体关系嵌入反向优化。如两图所示，当HyperMLN在同一数据集下结合相同推理方法时，同时使用变分E步和M步的效果一般要高于只使用变分E步的效果。这说明在变分EM训练后，同时使用推理模型和逻辑规则的效果要强于只使用推理模型进行预测的效果。在整合领域知识和语义信息的框架下，通过两者的配合可以达到最佳效果。

图5 知识超图数据集采用不同训练方式的预测结果

图6 知识图谱数据集采用不同训练方式的预测结果

由于可解释性是本框架的关键目标之一，在图7中提供了一个基于本框架进行结果解释的例子。与结果相关的元组首先从马尔科夫网络中提取预测元组的马尔科夫毯获得。概率为1.0的橘黄色元组是源数据集中的可观测元组，而概率不为1.0的两个浅黄色元组是通过推断所得的可观测元组。规则l1和l2的权重分别为0.7和0.2。现在要预测蓝色隐藏元组为真的概率，以及每个关系和实体对该元组为真的置信度。首先，根据关系类型，从规则集中选择与"父亲"关系相关的规则。然后，根据隐藏元组是否存在于两个规则的闭规则集中，从马尔科夫网络中抽取与隐藏元组相关的三个变量。根据两个闭规则分别构建两个团。之后，根据结果解释章节的公式求得隐藏元组为真的概率为0.32，其中家庭和爷爷关系的置信度分别为0.725和0.275，艾伦、丹尼尔、艾玛、朱莉和简的置信度分别为0.267、0.115、0.352、0.252和0.014。

图7  通过逻辑规则解释推理结果的示例

总结

在本文中，提出了一个新颖的框架，支持对基于多元关系的元组进行表示，将马尔科夫逻辑网络与知识超图嵌入方法相结合，基于马尔科夫毯解释推理结果。HyperMLN与大多数最先进的知识超图嵌入模型相结合，在相同的设置下可提升模型性能，并使用变分EM算法有效地学习语义和领域知识。

---

OpenKG

OpenKG（中文开放知识图谱）旨在推动以中文为核心的知识图谱数据的开放、互联及众包，并促进知识图谱算法、工具及平台的开源开放。

点击阅读原文，进入 OpenKG 网站。