stata中计算公式命令_Stata: 工具变量法 (IV) 也不难呀！
NEW！连享会·推文专辑：
Stata资源 | 数据处理 | Stata绘图 | Stata程序
结果输出 | 回归分析 | 时间序列 | 面板数据 | 离散数据
交乘调节 | DID | RDD | 因果推断 | SFA-TFP-DEA
文本分析+爬虫 | 空间计量 | 学术论文 | 软件工具
连享会学习群-常见问题解答汇总：
? WD 主页： https://gitee.com/arlionn/WD
? 连享会主页：lianxh.cn
Stata 暑期班：9天直播
? 时间：2020.7.28-8.7
? 嘉宾：连玉君 (中山大学) | 江艇 (中国人民大学)
? 主页：https://gitee.com/arlionn/PX | ? 微信版「基础不牢，地动山摇……」
彩蛋：现在报名「Stata暑期全程班」即可获赠 Stata Logo T恤一件，好拉风！
作者：杨柳 (西北大学)，连玉君 (中山大学)E-Mail: [email protected]，[email protected]
目录
1. IV 估计法的基本思想
2. IV 估计式
3. 2SLS
3.1 2SLS 原理
3.2 应用 Stata 计算示例
参考文献
王小二参加研究生复试的面试时，恰好认识其中一位参加面试的老师。假设面试分数 () 由面试老师 () 决定，王小二可视为随机误差项 ，认识王小二的那位面试老师可视为内生的解释变量 ，如果让这位老师继续参加面试给王小二打分，那么面试分数就很可能偏高。如何解决这个内生性问题呢？不妨再找另一个老师来代替这位跟王小二认识的老师，基本要求是：新找来的老师不能跟王小二认识，并且又跟被替换下的这位老师在专业背景方面有很高的相似度。这个新找来的老师就称为被替换下的老师的工具变量 (Instrumental Variable，简称 IV) 。接下来，让我们一起学习 IV 估计。
1. IV 估计法的基本思想
我们从一个最简单的回归模型引入工具变量估计法。如下式(1)所示：
假设 度量的是收入， 度量的是受教育的年数， 为随机误差项。简单回归模型(1)假设 与随机误差项 不相关。 对 的唯一直接影响是通过 带来的，如下图(1)所示：
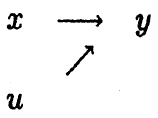图1 简单回归模型x对y的直接影响
随机误差项 包括了除受教育年数之外的所有其他未观测到的影响收入的因素，能力 的因素包括在 中，因为 能力 的高低与 收入 () 具有相关性(一般的，能力高的人收入会高)。但同时 能力 的高低与 受教育年数 () 也具有相关性(一般的，能力高的人倾向于接受更多的教育或技能培训)，如下图(2)所示：
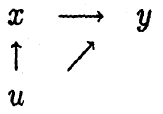图2 误差项与x相关
在模型(1)中我们遗漏了 能力 这个重要变量，在这种情况下，OLS 估计量 就不是 的一致估计量，因为 包括了两部分的影响效果：一部分 是我们期望得到的受教育年数对收入的直接影响，另一部分 是来自于能力的间接影响，例如，能力高的人通常会有较高的受教育年数，从而有较高的收入。如果受教育时间增加 1 年与年收入增加 1,000 美元相关，我们就不能确定增加的 1,000 美元当中有多少是来自于 受教育年数多的影响，有多少是来自于 能力高 的影响。
我们可以使用工具变量估计法解决上述内生性问题。引入一个新的工具变量 ，它具有以下性质： 的变化与 的变化相关；除了 会间接的通过影响 来影响 之外， 的变化不会导致 的变化。例如，与大学相邻 () 可能会决定是否上大学，从而影响受教育年数 ()，但并不直接决定收入 ()。如下图三所示：
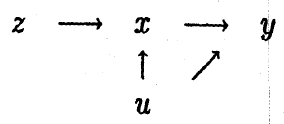图3 工具变量z的影响效果的图示
当 的工具变量 满足以下条件时，IV 估计量 是一致估计量： (1) 与 相关； (2) 与 不相关。
2. IV 估计式
在一般形式的回归模型(2)中(以矩阵形式表示)：
是由解释变量构成的 维矩阵， 是系数向量。定义一个矩阵 与 有着相同的维度，作为 的工具变量，将(2)式两端同乘以矩阵 ，则有：
工具变量 与 不相关，意味着当 趋于无穷大时 的概率极限为 0。因此，我们可以从下式中定义出 IV 估计量 ：
IV 估计量的一种有趣的情况是：如果零条件均值假设满足，每一个解释变量都可以做为自己的工具变量，即 ，此时，IV 估计量就缩减为 OLS 估计量。因此，当零条件均值假设满足时，OLS 估计量是 IV 估计量的一种特殊情形。
3. 2SLS
如果 "王小二面试" 时找来一个代替老师，那么这位新老师给的面试分数还是有一定的随机性，一个主要的原因是新找来的这位老师可能与被替换的那位老师之间的相关性不够强。为了控制面试得分偏差，我们可以多找几个老师。不妨找三个老师，这三个老师就称为被替换下来的老师的三个工具变量。此时，我们会面临一个问题：回归模型中有一个内生变量，并且我们找了多个工具变量，不妨设为 , , 三个工具变量。这时应该如何使用 IV 估计法？我们可以将 带入 IV 估计式 得到一个 IV 估计量 。如果我们重复上述步骤将 , 带入 IV 估计式，将得到另外两个 IV 估计量 , ，而这三个 IV 估计量是不一样的。这就又带来了一个问题，如何将这两个 IV 估计量整合为一个？
两阶段最小二乘估计法 (2SLS) 可以将多个工具变量整合为一个最优的工具变量，这样就可以应用到 IV 估计式中。
3.1 2SLS 原理
考虑简单回归模型(1)的情形：我们为内生变量 (受教育的年数) 找到了两个工具变量，分别为 与 。我们用 与 对 进行回归，如下式模型(3)所示：
得到用两个工具变量 与 预测的 。根据最小二乘法的原理， 是 与 中信息的最优线性组合。在接下来的第二阶段中，我们将 代入模型 (1) 中，得到的估计量就是 2SLS 估计量 。
为了说明 2SLS 法的计算原理，我们定义一个矩阵 ，维度为 ，，让它表示所有的工具变量。接下来进行第一阶段的回归，得到 与 的最优线性组合 ，可作为 的工具变量：
将上式代入 IV 估计式中可得：
定义投影矩阵 ，则上式可写为：
在上式中，2SLS 估计量可以用 ， 和 一次完成计算。当 时，2SLS 估计量缩减为 IV 估计量，因此，2SLS 的计算公式包含了 IV 估计式。
假设随机误差项 是独立同分布的，大样本条件下 2SLS 估计量的 VCE 的一致估计量为：
上式中，
其中， 为 2SLS 的残差，由初始的 ， 和 2SLS 的估计系数计算得到：
需要特别说明的是， 尽管 2SLS 法是按照两个阶段回归的顺序进行的 ，但是我们不能按照这两个阶段的顺序进行手动计算，因为如果这样做的话，第二个阶段的回归将得到错误的残差 ，而正确的残差是 。
使用 Stata 的 2SLS 法的命令
ivreg 2sls将避免上述错误。完成 2SLS 估计之后，使用predict命令将得到正确的残差值。
3.2 应用 Stata 计算示例
2SLS 命令语法
其中，ivregress 2sls 为 2SLS 的 Stata 命令； 为被解释变量； 为外生解释变量； 为所有的内生解释变量； 为所有的工具变量；在选项 中，可使用 选项计算稳健型标准误、可使用 选项报告 2SLS 中第一阶段的回归结果。
Stata 范例
示例 1：已婚妇女的教育回报(IVs：父母的受教育年数)
使用《计量经济学导论 现代观点》中的 mroz.dta 数据来研究已婚妇女的教育回报率。该份数据包括了在 1976 年调查的 753 个已婚妇女的年龄、工资与受教育的年数、丈夫的年龄、工资与受教育的年数、家庭收入、已婚妇女的父母的受教育年数、已婚妇女的工作经历年数等变量 (点击此处下载 mroz.dta 数据)。
我们用已婚妇女工资的对数值 (ln wage) 作为被解释变量，受教育年数 (educ) 、工作经历年数 (exper) 与工作经历年数的平方值 (expersq) 作为解释变量。现在，我们想研究教育的边际回报是多少，于是建立如下回归模型(4)：
在模型(4)中， 包括了所有其他未观测到的影响已婚妇女工资的因素，其中 能力 会对工资有正影响作用，但未包括在模型(3)中，我们遗漏了重要解释变量 能力 。并且，能力 与 educ 又是正相关的 ，这样解释变量 educ 是内生的，使用 OLS 估计法会导致估计量 是不一致的。
现在我们寻找 educ 的工具变量，进而使用 2SLS 法对 进行估计。一般常识认为，已婚妇女的 父亲和母亲的受教育年数 (motheduc 与 fatheduc) 跟已婚妇女的 educ 是正相关的，而这两个变量与已婚妇女的 能力 不是直接相关的。因此，我们可以用 motheduc 与 fatheduc 作为 educ 的工具变量。Stata 命令和结果如下所示：
. use "D:\stata15\ado\personal\IV_2SLS\Data\mroz.dta", clear
. *-Coviariates set up
. global aa "exper expersq"
. *-2SLS
. ivregress 2sls lwage $aa (educ = motheduc fatheduc)
Instrumental variables (2SLS) regression Number of obs = 428
Wald chi2(3) = 24.65
Prob > chi2 = 0.0000
R-squared = 0.1357
Root MSE = .67155
--------------------------------------------------------------------------
lwage | Coef. Std. Err. z P>|z| [95% Conf. Interval]
---------+----------------------------------------------------------------
educ | .0613966 .0312895 1.96 0.050 .0000704 .1227228
exper | .0441704 .0133696 3.30 0.001 .0179665 .0703742
expersq | -.000899 .0003998 -2.25 0.025 -.0016826 -.0001154
_cons | .0481003 .398453 0.12 0.904 -.7328532 .8290538
--------------------------------------------------------------------------
Instrumented: educ
Instruments: exper expersq motheduc fatheduc
将 2SLS法 与 OLS 法的回归结果进行比较，Stata 命令和结果如下所示：
. *-OLS
. reg lwage educ $aa
Source | SS df MS Number of obs = 428
----------+---------------------------------- F(3, 424) = 26.29
Model | 35.0223023 3 11.6741008 Prob > F = 0.0000
Residual | 188.305149 424 .444115917 R-squared = 0.1568
----------+---------------------------------- Adj R-squared = 0.1509
Total | 223.327451 427 .523015108 Root MSE = .66642
---------------------------------------------------------------------------
lwage | Coef. Std. Err. t P>|t| [95% Conf. Interval]
----------+----------------------------------------------------------------
educ | .1074896 .0141465 7.60 0.000 .0796837 .1352956
exper | .0415665 .0131752 3.15 0.002 .0156697 .0674633
expersq | -.0008112 .0003932 -2.06 0.040 -.0015841 -.0000382
_cons | -.5220407 .1986321 -2.63 0.009 -.9124668 -.1316145
---------------------------------------------------------------------------
. est store OLS
. *-2SLS
. ivregress 2sls lwage $aa (educ = motheduc fatheduc)
Instrumental variables (2SLS) regression Number of obs = 428
Wald chi2(3) = 24.65
Prob > chi2 = 0.0000
R-squared = 0.1357
Root MSE = .67155
--------------------------------------------------------------------------
lwage | Coef. Std. Err. z P>|z| [95% Conf. Interval]
---------+----------------------------------------------------------------
educ | .0613966 .0312895 1.96 0.050 .0000704 .1227228
exper | .0441704 .0133696 3.30 0.001 .0179665 .0703742
expersq | -.000899 .0003998 -2.25 0.025 -.0016826 -.0001154
_cons | .0481003 .398453 0.12 0.904 -.7328532 .8290538
--------------------------------------------------------------------------
Instrumented: educ
Instruments: exper expersq motheduc fatheduc
. est store _2SLS
. *-输出回归结果(屏幕显示结果)
. local m "OLS _2SLS"
. esttab `m', mtitle(`m') replace ///
> nogap compress b(%6.3f) s(N r2_a) se ///
> star(* 0.1 ** 0.05 *** 0.01) ///
> addnotes("*** 1% ** 5% * 10%")
------------------------------------
(1) (2)
OLS _2SLS
------------------------------------
educ 0.107*** 0.061**
(0.014) (0.031)
exper 0.042*** 0.044***
(0.013) (0.013)
expersq -0.001** -0.001**
(0.000) (0.000)
_cons -0.522*** 0.048
(0.199) (0.398)
------------------------------------
N 428.000 428.000
r2_a 0.151 0.130
------------------------------------
Standard errors in parentheses
*** 1% ** 5% * 10%
* p<0.1, ** p<0.05, *** p<0.01
从上面的结果中可以看到，使用
2SLS估计的受教育年数的边际回报为6.1%，而使用OLS估计的受教育年数的边际回报为10.7%。两者具有差异，OLS的估计值偏高。但是我们并不知道两者的差异是否在统计上显著？哪个系数估计值更接近于真实的教育回报？在随后的推文中，我们将介绍对工具变量的合理性与解释变量的内生性进行检验，敬请期待。
我们还看到，
2SLS结果中educ的标准误是OLS结果的 2.21 倍(2SLS估计的方差总是大于OLS的方差，证明见《计量经济学导论 现代观点》第十五章)，表明若模型中没有内生性问题，OLS 的估计结果更有效。
示例 2：男性样本的教育回报(IV：是否在大学附近成长)
使用《计量经济学导论 现代观点》中的 card.dta 数据来研究一份男性样本的教育回报率。该份数据包括了在 1976 年调查的 3010 位男性的年龄、工资与受教育的年数、父母的受教育年数、工作经历年数、居住地的区域(南部/大城市及其郊区/其他地区)、是否在四年制/两年制大学附近成长、种族(是否黑人)等变量 (点击此处下载 card.dta 数据)。 使用受教育年数 (educ) 和其他控制变量：工作经历年数 (exper) 及其平方项 (expersq)、黑人种族虚拟变量 (black)、居住在大城市及其郊区 (smsa) 、居住在南部 (south) 和其他居住地区域的虚拟变量 (smsa66, reg662, reg663, reg664, reg665, reg667, reg668, reg669) 建立回归模型(5)，如下所示：
模型中遗漏了 能力 变量，带来了 educ 变量是内生的问题。卡德(Card，1995)为 educ 选择的工具变量为：一个人是否在一所四年制大学附近成长 (nearc4) 的虚拟变量，认为该变量与 能力 无直接关系，并且与 educ 变量正相关(若一个人在四年制大学附近成长，那么受教育的年数会更多一些)。使用 IV 估计法对参数 的值进行求解，并将该结果与 OLS 进行对比，Stata命令和结果如下：
. use "D:\stata15\ado\personal\IV_2SLS\Data\card.dta", clear
. *-Coviariates set up
. global bb "exper expersq black smsa south smsa66 reg662 reg663 reg664 reg665 reg666 reg667 reg668 reg669"
. *-OLS
. reg lwage educ $bb
Source | SS df MS Number of obs = 3,010
----------+---------------------------------- F(15, 2994) = 85.48
Model | 177.695576 15 11.8463717 Prob > F = 0.0000
Residual | 414.946035 2,994 .13859253 R-squared = 0.2998
----------+---------------------------------- Adj R-squared = 0.2963
Total | 592.641611 3,009 .196956335 Root MSE = .37228---------------------------------------------------------------------------
lwage | Coef. Std. Err. t P>|t| [95% Conf. Interval]
----------+----------------------------------------------------------------
educ | .0746932 .0034983 21.35 0.000 .0678338 .0815527
exper | .084832 .0066242 12.81 0.000 .0718435 .0978205
expersq | -.002287 .0003166 -7.22 0.000 -.0029079 -.0016662
black | -.1990123 .0182483 -10.91 0.000 -.2347928 -.1632318
smsa | .1363846 .0201005 6.79 0.000 .0969724 .1757967
south | -.147955 .0259799 -5.69 0.000 -.1988952 -.0970148
smsa66 | .0262417 .0194477 1.35 0.177 -.0118905 .0643739
reg662 | .0963671 .0358979 2.68 0.007 .0259801 .1667542
reg663 | .14454 .0351244 4.12 0.000 .0756695 .2134104
reg664 | .0550755 .0416573 1.32 0.186 -.0266043 .1367554
reg665 | .1280248 .0418395 3.06 0.002 .0459878 .2100618
reg666 | .1405174 .0452469 3.11 0.002 .0517992 .2292356
reg667 | .117981 .0448025 2.63 0.008 .0301343 .2058277
reg668 | -.0564361 .0512579 -1.10 0.271 -.1569404 .0440682
reg669 | .1185697 .0388301 3.05 0.002 .0424334 .194706
_cons | 4.620807 .0742327 62.25 0.000 4.475255 4.766359
---------------------------------------------------------------------------
. est store OLS_nearc4
. *-2SLS
. ivregress 2sls lwage $bb (educ = nearc4)
Instrumental variables (2SLS) regression Number of obs = 3,010
Wald chi2(15) = 769.20
Prob > chi2 = 0.0000
R-squared = 0.2382
Root MSE = .3873
--------------------------------------------------------------------------
lwage | Coef. Std. Err. z P>|z| [95% Conf. Interval]
---------+----------------------------------------------------------------
educ | .1315038 .0548174 2.40 0.016 .0240637 .2389439
exper | .1082711 .0235956 4.59 0.000 .0620245 .1545176
expersq | -.0023349 .0003326 -7.02 0.000 -.0029868 -.001683
black | -.1467758 .0537564 -2.73 0.006 -.2521364 -.0414152
smsa | .1118084 .0315777 3.54 0.000 .0499172 .1736996
south | -.1446715 .027212 -5.32 0.000 -.198006 -.0913369
smsa66 | .0185311 .0215511 0.86 0.390 -.0237083 .0607704
reg662 | .1007677 .0375854 2.68 0.007 .0271017 .1744338
reg663 | .1482588 .0367162 4.04 0.000 .0762964 .2202211
reg664 | .0498971 .0436234 1.14 0.253 -.0356032 .1353974
reg665 | .1462719 .0469387 3.12 0.002 .0542737 .23827
reg666 | .1629029 .0517714 3.15 0.002 .0614328 .264373
reg667 | .1345722 .0492708 2.73 0.006 .0380031 .2311412
reg668 | -.083077 .0591734 -1.40 0.160 -.1990548 .0329008
reg669 | .1078142 .0417024 2.59 0.010 .026079 .1895494
_cons | 3.666152 .9223682 3.97 0.000 1.858344 5.47396
--------------------------------------------------------------------------
Instrumented: educ
Instruments: exper expersq black smsa south smsa66 reg662 reg663 reg664
reg665 reg666 reg667 reg668 reg669 nearc4
. est store _2SLS_nearc4
. *-输出回归结果(屏幕显示结果)
. local m "OLS_nearc4 _2SLS_nearc4"
. esttab `m', mtitle(`m') replace ///
> nogap compress b(%6.3f) s(N r2_a) se ///
> star(* 0.1 ** 0.05 *** 0.01) ///
> addnotes("*** 1% ** 5% * 10%")
------------------------------------
(1) (2)
OLS_nea~4 _2SLS_n~4
------------------------------------
educ 0.075*** 0.132**
(0.003) (0.055)
exper 0.085*** 0.108***
(0.007) (0.024)
expersq -0.002*** -0.002***
(0.000) (0.000)
black -0.199*** -0.147***
(0.018) (0.054)
smsa 0.136*** 0.112***
(0.020) (0.032)
south -0.148*** -0.145***
(0.026) (0.027)
smsa66 0.026 0.019
(0.019) (0.022)
reg662 0.096*** 0.101***
(0.036) (0.038)
reg663 0.145*** 0.148***
(0.035) (0.037)
reg664 0.055 0.050
(0.042) (0.044)
reg665 0.128*** 0.146***
(0.042) (0.047)
reg666 0.141*** 0.163***
(0.045) (0.052)
reg667 0.118*** 0.135***
(0.045) (0.049)
reg668 -0.056 -0.083
(0.051) (0.059)
reg669 0.119*** 0.108***
(0.039) (0.042)
_cons 4.621*** 3.666***
(0.074) (0.922)
------------------------------------
N 3010.000 3010.000
r2_a 0.296 0.234
------------------------------------
Standard errors in parentheses
*** 1% ** 5% * 10%
* p<0.1, ** p<0.05, *** p<0.01
我们看到上述结果中有趣的一点是：OLS 估计的教育回报的边际效应是
7.5%，约为 IV 估计的13.2%的一半，带来的直观结果是 OLS 并没有高估教育回报。而我们在理论分析中通常认为由于遗漏了能力这个重要变量，OLS 会高估教育对工资的边际回报。Card 在 1993 年发表了使用是否在大学附近成长作为工具变量研究教育回报率的文章，在后续推文中，我们将详细介绍这个文献案例，敬请关注。
参考文献
- Christopher F. Baum (2006). An Introduction to Modern Econometrics Using Stata.
- A. Colin Cameron and Pravin K. Trivedi (2009). Microeconometrics Using Stata.
- Wooldridge, J. M. (2012). Introductory Econometrics A Modern Approach.
连享会 - 文本分析与爬虫 - 专题视频， 微信版
主讲嘉宾：司继春 || 游万海
连享会-文本分析与爬虫-专题视频教程
连享会 - 效率分析专题
已上线：可随时购买学习+全套课件，课程主页 已经放置板书和 FAQs
主讲嘉宾：连玉君 | 鲁晓东 | 张宁
课程主页，微信版 https://gitee.com/arlionn/TE
连享会-效率分析专题视频
? ? ? ?
连享会主页： ? www.lianxh.cn
直播视频： lianxh.duanshu.com
免费公开课：
- 直击面板数据模型：https://gitee.com/arlionn/PanelData - 连玉君，时长：1小时40分钟
- Stata 33 讲：https://gitee.com/arlionn/stata101 - 连玉君, 每讲 15 分钟.
- 部分直播课课程资料下载 ? https://gitee.com/arlionn/Live (PPT，dofiles等)
温馨提示： 文中链接在微信中无法生效。请点击底部
关于我们
- ? 连享会 ( 主页：lianxh.cn ) 由中山大学连玉君老师团队创办，定期分享实证分析经验。
- ? 直达连享会：【百度一下：连享会】即可直达连享会主页。亦可进一步添加 主页，知乎，面板数据，研究设计 等关键词细化搜索。
- ? 公众号推文分类： 历史推文分为多个专辑，主流方法介绍一目了然：DID, RDD, IV, GMM, FE, Probit 等。
连享会 · 推文专辑：
Stata资源 | 数据处理 | Stata绘图 | Stata程序
结果输出 | 回归分析 | 时序 | 面板 | 离散数据
交乘调节 | DID | RDD | 因果推断 | SFA-TFP-DEA
文本分析+爬虫 | 空间计量 | 学术论文 | 软件工具 - ❓ 公众号关键词搜索/回复 功能已经上线。大家可以在公众号左下角点击键盘图标，输入简要关键词，以便快速呈现历史推文，获取工具软件和数据下载。
连享会主页 lianxh.cn
Stata 暑期班：9天直播
? 时间：2020.7.28-8.7
? 嘉宾：连玉君 (中山大学) | 江艇 (中国人民大学)
? 主页：https://gitee.com/arlionn/PX | ? 微信版「基础不牢，地动山摇……」
