多方安全计算中半诚实模型下的姚式混淆电路协议
在MPC(多方安全计算)中,有一个叫做半诚实模型的概念,区分于“主动攻击”的恶意敌手,半诚实模型的参与方仅在计算时保存了协议的中间计算状态(即输入输出),其在MPC中也具有一定的危害性。
本博客讲解了在Yao’s protocol双方安全计算协议下的半诚实模型攻击者的攻击手法。
目录
- 1 多方安全计算 MPC
- 2 半诚实敌手 semi-honest adversary
- 3 混淆电路 garbled circuit
-
- 问题的引出
- 如何构造混淆电路
- 计算混淆电路
- 4 基于半诚实模型的姚式协议 Yao's protocol for semi-honest adversary
-
-
- 一元富翁
-
1 多方安全计算 MPC
MPC简单来说,就是一堆人想要用自己和别人手上的隐私数据来计算一些东西(比如一个函数),但每一个人都不想让其他人知道自己的隐私数据是什么。
而双方安全(2PC),便是MPC的特殊情况。如下图,其中只有两个人(Alice and Bob)想用自己的隐私数据(x)和对方的隐私数据(y)一起计算一个函数f,同时不想让对方知道自己的数据输入。
2 半诚实敌手 semi-honest adversary
依然在双方安全的语境下,如果有其中一方时半诚实敌手,此处假设是y方。在遵守协议的前提下,y会希望能获取到x的输入。这样的一方被称为半诚实敌手。
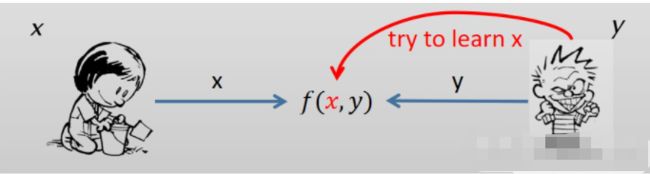
注意,虽然 敌手y 很想获取到 参与者x 的输入,但一定会遵守双方的计算协议。
3 混淆电路 garbled circuit
混淆电路 在整个加密计算过程中不会出现能解密出两个及以上的有意义的值的情况,因此具有相当高的保密性,我们来具体了解一下什么是混淆电路。
它的核心技术是将两方参与的安全计算函数编译成布尔电路的形式,并将真值表加密打乱,从而实现电路的正常输出而又不泄露参与计算的双方私有信息。由于任何安全计算函数都可转换成对应布尔电路的形式,相较其他的安全计算方法,具有较高的通用性,因此引起了业界较高的关注度。
首先我们设想,对于一个函数,我们能不能用“不真实”的输入(以此作为混淆),得到真实的结果?
我们可否建立一个这样的映射,对于我们的每个输入,与其使用真实输入参与函数计算,我们为每个输入构造一个“替身”,让这个替身为其完成计算的任务。
下面我们就来介绍姚期智院士在1986年提出的混淆电路是如何解决这个问题的。
我们知道,任何函数都可以被表示为一个门电路,计算一个函数其实就是计算一个门电路,得到电路输出的过程。一个门电路是由许多个门组成的,我们这里先用只由一个门组成的电路来解释混淆电路的原理。
问题的引出
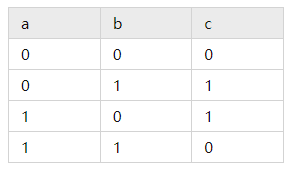
比如有一个计算两个1 bit数a,b模2加法的函数 f ( a , b ) f(a,b) f(a,b),则我们可以用下面的电路来表示。
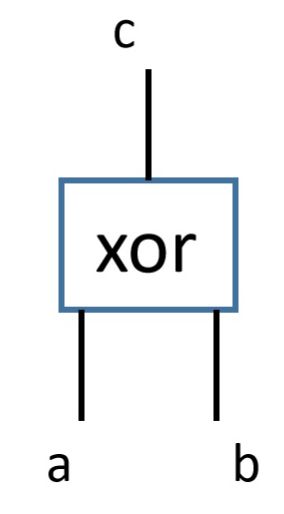
这个电路很简单,只有一个异或门,给电路提供两个输入a和b,其输出一个结果c。
如果直接在此种场景下计算,a和b输出的都是表示真实意义的真值,而如果b一旦知道此函数的计算方法,就可以根据 f ( a , b ) 和 b f(a,b)和 b f(a,b)和b,反推出a的值,这样就出现了隐私的泄露。那么,我们是不是可以对这整个计算流程进行加密,防止这样的隐私泄露呢?
.
如何构造混淆电路
下面,我们来基于这个电路(其实只有一个异或门),来构造一个混淆电路。
可以看出,电路中有三条线(两条输入线a、b,一条输出线c),我们将其标为 w 1 、 w 2 、 w 3 w_1、w_2、w_3 w1、w2、w3。
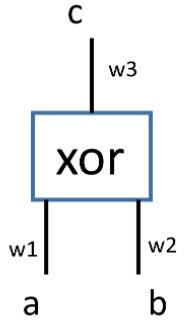
每条线上可能会存在两种逻辑值——0和1,我们想隐藏每条线上真实的逻辑值(不想让别人知道现在是0还是1在这条线上),可以通过以下的步骤来实现。
1.首先,为电路中所有线路分配两个分别代表逻辑值0和1的密钥。记一条线路(即加密后的数值)为 w i w_i wi ,则为其分配两个密钥记为 k i b , b ∈ { 0 , 1 } k_i^b,b \in\{0,1\} kib,b∈{0,1} 。b为0则此密钥代表的逻辑值为0,为1则代表的逻辑值为1。
回到上面那个例子,电路中只有三条线路,则对线路 w 1 w_1 w1,其有密钥 k 1 0 k_1^0 k10 和 k 1 1 k_1^1 k11 ;对线路 w 2 w_2 w2,其有密钥 k 2 0 k_2^0 k20 和 k 2 1 k_2^1 k21 ;对线路 w 3 w_3 w3,其有密钥 k 3 0 k_3^0 k30 和 k 3 1 k_3^1 k31 。(这里提一下,因为 w 3 w_3 w3 为输出线路,所以不一定要为其生成密钥,但这里暂时与其他线路保持一致,具体原因后面解释)。
2.对电路中的每个门,我们使用上述密钥和门的真值表,对门的输出进行加密。
这一步骤的具体操作如下:
我们直接通过上述例子来理解加密步骤。例子中,我们的电路只有一个门,所以只需要对这个门进行加密。我们将上面真值表的a,b,c 换为 w1,w2,w3,以表示这个门对应的三条线路,其中w3为输出线路,我们对其进行加密。
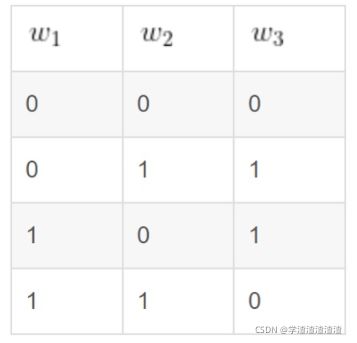
对真值表的每一行,我们将输入线w1和w2的逻辑值替换成对应的密钥值。
用w1和w2的密钥值,对w3的逻辑值对应的密钥值进行加密,将w3替换为该加密值。
如第一行,w1上的0替换为 k 1 0 k_1^0 k10,w2上的0替换为 k 2 0 k_2^0 k20,w3上的0替换为 k 3 0 k_3^0 k30后,用 k 1 0 k_1^0 k10 和 k 2 0 k_2^0 k20
通过加密算法 E n c Enc Enc 加密得到 E n c k 1 0 , k 2 0 ( k 3 0 ) Enc_{k_1^0,k_2^0}(k_3^0) Enck10,k20(k30) 。
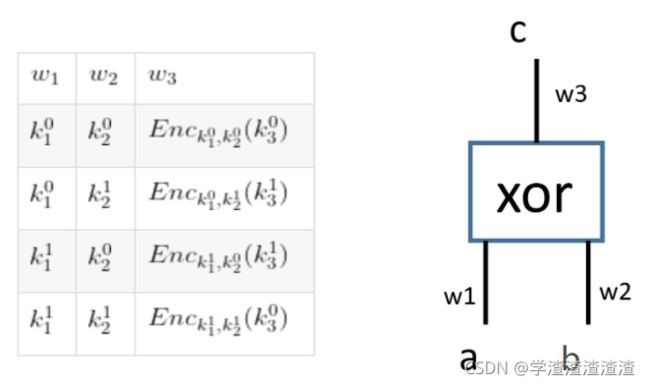
其他三行也是如此操作。最后生成的表如下图的右表格:
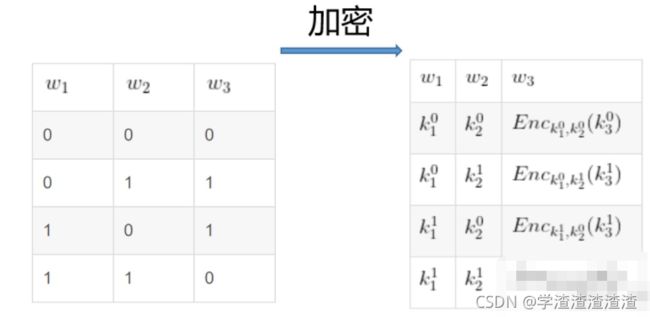
3. 然后,我们将表中的行进行随机置换,打乱原来行的排布。这步非常关键,因为这样一来,行的位置便不包含任何信息。(若不打乱,则我们能知道表的每一行的加密值是由哪两个逻辑值加密而来的)。这一步称为混淆(garbled)。下图的右表格即为混淆后的表。
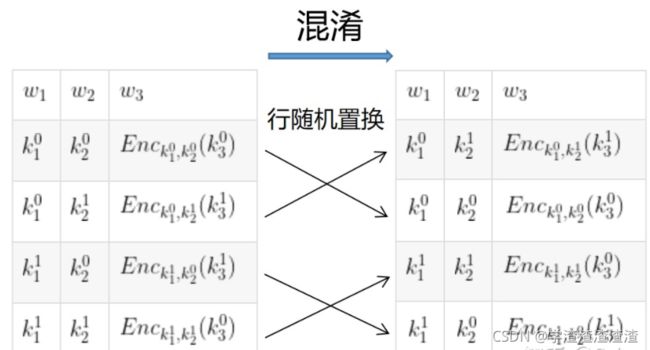
4. 最后,取出上表的第三列,得到这个电路最终的混淆表。注意,其实这只是一个门的混淆表,但因为我们这个电路中只有这一个门,所以便也是这个电路的混淆表。若电路中不只有一个门,我们要为电路中的所有门都构造一个不同的混淆表,所有门的混淆表组合而成的才是整个电路的混淆表。
注意,因为我们是构造此混淆电路的人,所以我们知道上表的含义(每行的密文代表的是什么输出)。但对于单纯只是拿到此表的人(未参与GC构造的人,即各参与方,参与方按照混淆表的顺序进行输入,但是不知道加密后的输出代表什么含义),对此表每行所代表的信息是一脸懵逼的。
最后,因为我们要为电路的输出提供一个映射表。在这个例子中,w3的输出即为电路的输出。因为w3输出的v仍是密钥值,我们需要提供将其转化为真实值的映射。
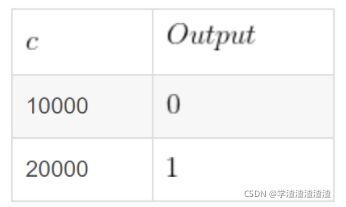
至此,我们的混淆电路——一个原始电路与电路的混淆表,就构造完毕了。那么我们该怎么来计算混淆电路呢?
计算混淆电路
若我们要计算原始电路,我们需要为电路的每条输入线提供真实的逻辑值0或1,才能得到真实的结果。但现在在混淆电路中,我们要为电路提供的不是真实的逻辑值,而是每条输入线上逻辑值所对应的密钥值!
我们用我们刚刚为计算函数 f f f 构造的混淆电路(一个异或门与它的混淆表)来解释。为方便展示,左表是未混淆前的表格。

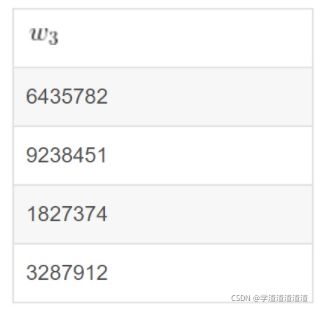
w1上的逻辑值0和1分别对应密钥1111和2222;w2上的逻辑值0和1分别对应密钥3333和6666;w3上的逻辑值0和1分别对应密钥10000和20000。而加密算法就是简单的将输入线的值与输出线的值相加。
(注意,真实情况的密钥是随机选取,加密算法也不可能如此retarded,此处是为了简化)
现在,我们将上表混淆(行打乱)后,提取出第三列。
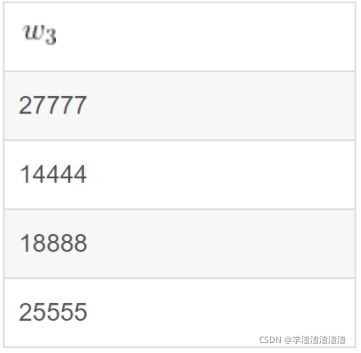
最后,我们定义了输出密文与真实值的映射。有了以下信息,我们就能完成计算。

现在假设输入 a = 1111 a=1111 a=1111, a = 6666 a=6666 a=6666,此时a和b是真实输入的密钥值。我们想知道输出 c c c 是什么。
现在我们有混淆表,而表中的值就是电路输出的密文,我们得通过解密才能还原我们对应输入的真实值。我们知道加密算法是 a + b + c a+b+c a+b+c,则我们可以解密还原出真实值。那么表中的哪个值才是我们应该解密的值呢?很简单,我们遍历表中的四个值进行解密计算,若计算出的值没有意义,则不是我们要的值。
对表中的第一行, 27777 − 1111 − 6666 = 20000 27777-1111-6666 = 20000 27777−1111−6666=20000,对照输出映射表,即对应真实值1,于是我们得到了电路的输出为1。
这里有个点需要特别注意:我们构造混淆电路的加密算法保证混淆表中不会(以很小概率)出现能解密出两个有意义的值的情况!
至此,我们完成了电路的计算,而且我们并没有输入a和b的真实值!
4 基于半诚实模型的姚式协议 Yao’s protocol for semi-honest adversary
现在,我们可以非形式化的定义姚式协议,基于半诚实模型的2PC协议。
现在假设Alice和Bob想基于姚式协议共同计算一个函数 f ( x , y ) f(x,y) f(x,y) ,其中 x x x 是Alice对函数的输入, y y y 是Bob对函数的输入。协议可以简单的分为以下几步:
在了解以前,我们先定义一个概念,混淆值 (若 z z z为明文则 z ^ \hat{z} z^为加密后的混淆值):指对明文(即真值)进行加密后的密钥。
1.构造电路:假设f是需要计算的函数,Alice构造对应的布尔电路(用1表示真,0表示假),这个电路有两个输入,分别为Alice和Bob的输入。
2.混淆电路:Alice混淆布尔电路中的每一个逻辑门运算的真值表,隐藏布尔电路的输入和输出之间的对应关系。对混淆的结果,只保留列 z ^ \hat{z} z^,并打乱行顺序,生成混淆表。
3.Alice将电路发给Bob:Alice把混淆表和Alice的输入值(加密后的混淆值)发送给Bob。
4.Alice将自己选择的混淆值告知Bob,并将Bob需要的两种混淆值对应的布尔值告知Bob(Alice知道Bob的混淆值和真值的对应关系,但是不知道Bob到底输入了哪个混淆值)。
5.Bob计算电路值:Bob用真值表和混淆的输入计算输出值。使用Alice和Bob的输入对应的 x ^ \hat{x} x^ 和 y ^ \hat{y} y^ ,解密混淆表的每一个值,只有一个能够成功解密,结果为 z ^ \hat{z} z^ 。再将 z ^ \hat{z} z^ 发给Alice,Alice即可还原出混淆值 z ^ \hat{z} z^ 对应的布尔值 z z z (Alice可查询完整的混淆表)。最后Alice可以将明文计算结果以安全方式告知Bob。
因为电路是Alice构造的,所以Bob不知道Alice的输入密钥所对应的逻辑值是什么,所以Bob并不知道Alice的真值输入。同理,Alice只知道最终的结果输出(输出的混淆值及其对应的明文),并不知道Bob输入的混淆值和真值。
我们用一个经典的例子来说明混淆电路是如何使用的。
一元富翁
问题:假设富翁Alice和Bob的资产数量都只有1bit(0元或1元),需要在不泄露两位富翁的资产数量的前提下,知道Alice的资产是否比Bob多。
条件:Alice的资产为0元,Bob的资产为1元。他们互相不知道对方的资产数量。
1.构造电路:Alice根据计算函数f,构建下图电路:
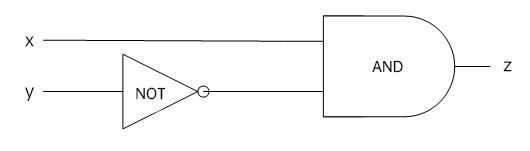
其中,Alice的资产值记作x,Bob的资产值记作y,结果记作z。当z=1时,Alice的资产大于Bob的;当z=0时,Alice的资产小于或等于Bob的资产数量。
该电路的真值表如下表所示:
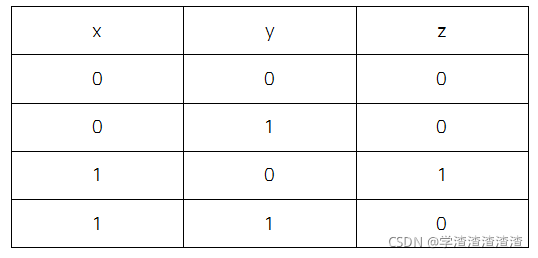
2. 构造混淆电路:将上述真值表转换为混淆表,混淆表的形式如下表所示:
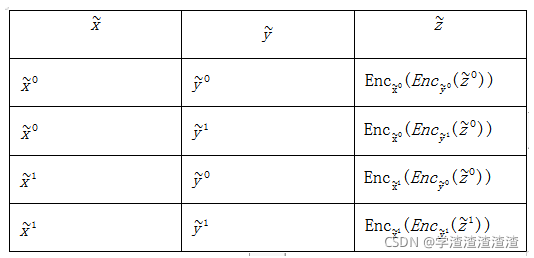
在计算中,Alice对各个混淆值取随机密钥。其中加密算法选择AES-256,以下密钥为base64编码后的内容:

由此计算出:
 所以需要发送给Bob的混淆表,形式为:(已经打乱过行顺序)
所以需要发送给Bob的混淆表,形式为:(已经打乱过行顺序)
4.Alice根据自己的秘密——她的资产是0,选择了混淆值:nQ0DEzHK+KdXOj7Dg0gMa4u6H5TGCHozql2NLQMK5l8=,并且告知Bob她选择了哪个混淆值。(注意Bob并不知晓这个混淆值代表0还是1,所以Bob并不知道Alice的秘密。)
并且Alice告知Bob,对于Bob来说,OOvRuZiaRe33Sf3caHNHM/8k8llr2RVdJlnQ0w2AoCM=代表布尔值0;混淆值AvsOttGzuHT3T7/oC0FQewQqq2ysCZvynMO+2fXjQNw=代表布尔值1。
5.Bob根据自己的秘密——他的资产是1,选择了混淆值AvsOttGzuHT3T7/oC0FQewQqq2ysCZvynMO+2fXjQNw=。
对于表3的每一行,使用两个输入混淆值。
(nQ0DEzHK+KdXOj7Dg0gMa4u6H5TGCHozql2NLQMK5l8=和AvsOttGzuHT3T7/oC0FQewQqq2ysCZvynMO+2fXjQNw=)对该结果做两次对称解密。
四行中仅有一行能够解密成功,解密成功的计算结果为Wn9pYEg4D7uv5ioT3X6DFLVDTkT7aBrfGY6wOYbLhHY=。
Bob将此结果发送给Alice,
Alice查对应关系可得,计算结果为z=0。
对应的,Alice的资产少于等于Bob的。
计算完成。
由示例过程可知,在全过程中,Alice无法知道Bob的选择,于是无法知晓Bob的秘密。而Bob无法知晓Alice的混淆值对应哪个比特,也无法知晓Alice的秘密。但Alice与Bob共同计算出了结果。
参考:
https://zhuanlan.zhihu.com/p/392860543
https://blog.csdn.net/weixin_28518991/article/details/113490679