【2022年高教杯数学建模】C题：古代玻璃制品的成分分析与鉴别方案及代码实现（一）

1.问题1：

对这些玻璃文物的表面风化与其玻璃类型、纹饰和颜色的关系进行分析；结合玻璃的类型，分析文物样品表面有无风化化学成分含量的统计规律，并根据风化点检测数据，预测风化前的化学成分含量。

2.问题1的分析

首先需要对玻璃表面风化情况与玻璃类型、纹饰和颜色的关系进行分析，选择的方式为差异性分析，接下来结合玻璃的类型分析化学成分含量的变化规律以及预测风化前的化学成分含量。
第一步分析：分析玻璃文物表面风化情况与玻璃类型、纹饰和颜色的关系进行分析，分析关系有相关性分析和差异性分析，根据提供的附件数据，不难看出玻璃类型、纹饰和颜色均属于定类数据，并非连续变量，因此进行卡方检验分析来确定变量之间的关系，利用SPSS软件进行求解，最后分析显著性 值是否小于0.05，进而分析差异性关系。

第二步分析：基于这些玻璃文物的类型，分析文物样品表面有无风化化学成分含量的统计规律；对于类型，只有高钾玻璃和铅钡玻璃两种；接下来分别讨论高钾玻璃与铅钡玻璃风化前后的变化差异进行描述性统计分析，做出频率分布直方图等，总结变化情况。

第三步分析：根据风化前后的数据规律，总结出各个化学成分的变化情况，使用加权平均法找到其映射关系并预测风化前的含量。

3.问题1模型的建立与求解

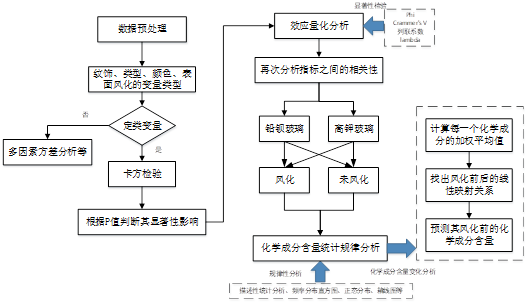
首先需要对玻璃表面风化情况与玻璃类型，纹饰和颜色的差异性进行分析，并结合玻璃的类型分析化学成分含量的变化规律以及预测风化前的化学成分含量，共需解决三个小问题，问题一建模分析流程图如下图所示:

3.1数据预处理

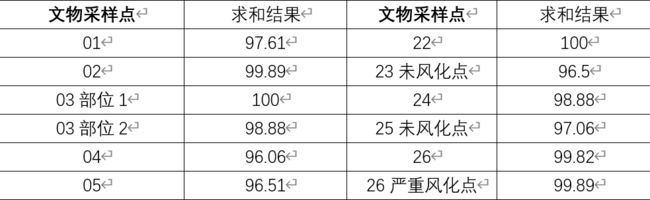
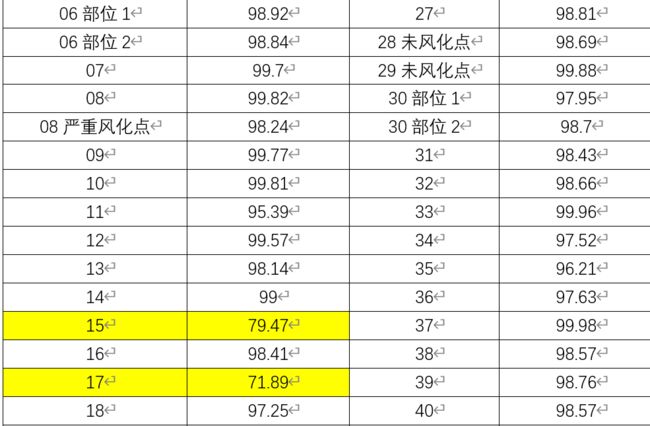
第一步处理：附件表单2中给出了玻璃文物主要化学成分所占的比例，空白处表示未检测到该成分。因为是比例，所以各成分比例的累加和应该为100%。根据题目要求，成分比例累加和介于85%-100%之间的数据视为有效数据，而低于85%的数据，应该视为异常值剔除。

我们对所有化学成分求和，部分结果如下表所示:

我们可以直观的看到，第15号采样点和第17号采样点的各成分累加值低于85%，属于无效数据，需要剔除。

第二步处理：附件表单1中颜色列中的数据中，我们发现有四个空值，通过观察数据变化情况发现颜色的深浅程度与风化程度呈现正相关变化，因此我们将四个空值进行填补，填补为“黑色”。

第三步处理：附件表单2给出了相应的主要化学成分所占比例，空白处根据题意表示未检测到该成分，因此我们将未检测到的数据进行补“0”处理，方便接下来的计算。

3.2表面风化的卡方检验

分析变量之间的关系，我们一般采用相关分析和差异性分析。通过观察表单1的数据，我们发现纹饰、类型、颜色、表面风化均为定类变量，此时计算相关系数并不合适，针对多组定类变量之间的差异性分析我们采用卡方检验。

卡方检验就是统计样本的实际观测值与理论推断值之间的偏离程度，实际观测值与理论推断值之间的偏离程度就决定卡方值的大小，如果卡方值越大，二者偏差程度越大；反之，二者偏差越小；若两个值完全相等时，卡方值就为0，表明理论值完全符合。

卡方检验的基本步骤如下：

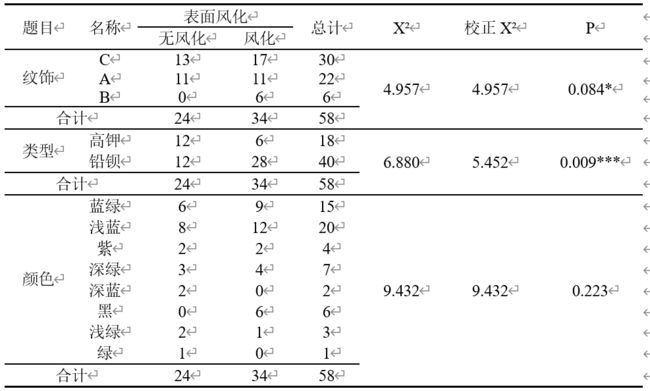
首先根据列联表分析进行变量的分组描述，部分结果展示如下：


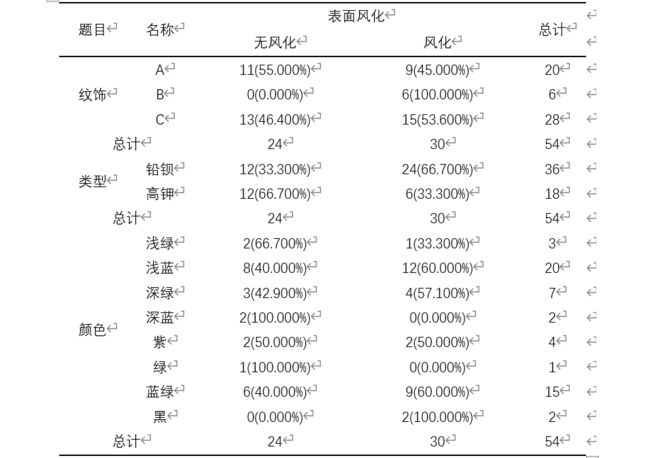
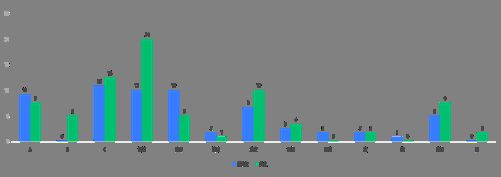
上表展示了以表面风化为分组项，以纹饰、类型、颜色为分析项的列联交叉分析结果，包括变量、频数、百分比等。通过结果我们可以初步看出，纹饰 的风化程度更高，铅钡玻璃的风华率远大于高钾玻璃的风华率，颜色的深度和风化呈现正相关的关系，颜色越深，风化程度越大。

基于上述描述，为了分析分组项下，各分析项是否存在差异以及差异的程度，我们设表面风化为变量 ，纹饰、类型、颜色为变量 ，使用SPSS软件对附件中的数据进行分析，得出如下表所示的卡方检验表。

由上表卡方检验的分析结果可以得出：表面风化和纹饰之间的显著性$p$值为0.084，接受原假设，因此不存在显著性差异；表面风化和类型之间的显著性$p$值为0.009，拒绝原假设，存在显著性差异；表面风化和颜色之间的显著性$p$值为0.223，接受原假设，因此不存在显著性差异。

在此基础上进行效应量化分析，包括phi、Crammer’s V、列联系数、lambda，用于分析表面风化与其余三个指标的相关程度，量化分析指标解释如下：

① phi系数：phi相关系数的大小表示两样本之间的关联程度。当phi系数小于0.3时，表示相关较弱；当phi系数大于0.6时，表示相关较强。

② Crammer’s V：与phi系数作用相似，但Crammer’s V系数的作用范围较广。

③ 列联系数：简称C系数

④ lambda：用于反映自变量对因变量的预测效果。

使用SPSS进行操作，得出结果如下表：

由上表效应量化分析的结果可以得出：纹饰Crammer’s V系数值为0.292，因此纹饰和表面风化的差异程度为中等程度差异；同理，玻璃类型的Crammer’s V系数值为0.344，为中等差异程度；颜色的Crammer’s V系数值为0.403，为中等程度差异。

由phi值可以分析出：纹饰、颜色、玻璃类型中纹饰的phi值小于0.3，说明纹饰与表面风化的相关性较弱，颜色与玻璃类型的phi值介于0.3至0.6之间，说明其相关程度为中等。

3.3不同玻璃类型表面有无风化统计规律分析

首先，对总体的各项统计指标进行整体描述分析，由于篇幅原因，这里仅展示铅钡玻璃的结果，如下表所示：

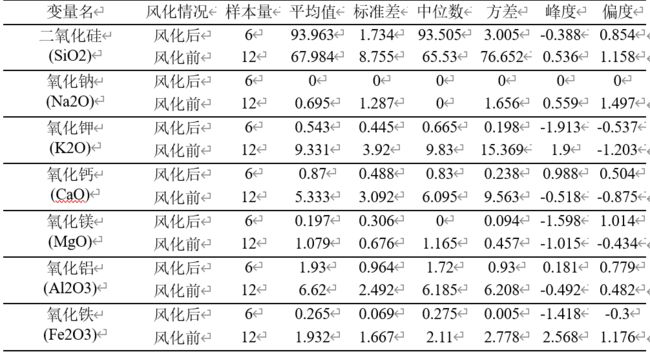
接着，我们筛选出高钾玻璃和铅钡玻璃各种化学成分风化前后相对重要的化学成分散点图进行分析：

高钾玻璃风化前后不同化学成分频率分布直方图:

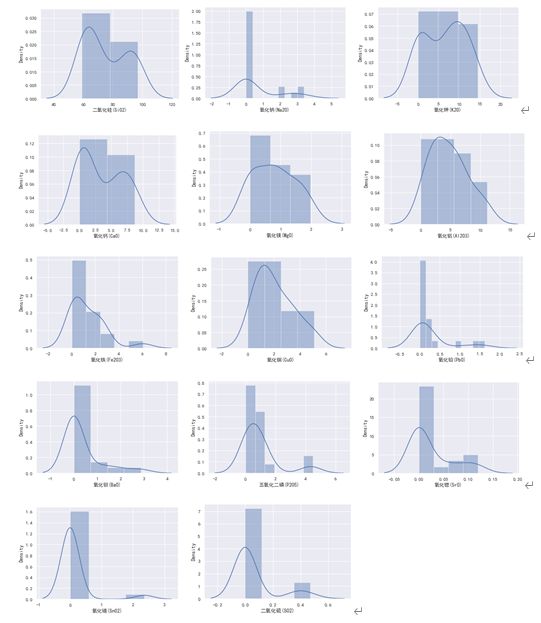
高钾玻璃的散点图：


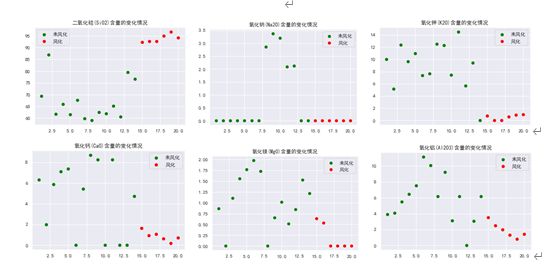
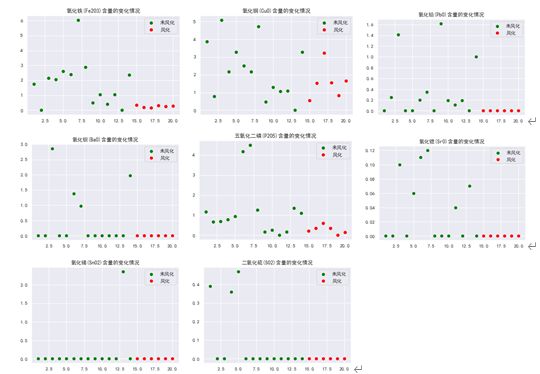
由频率分布直方图可以直观的看出高钾类玻璃在风化后主要化学成分含量呈下降趋势。

由高钾类玻璃各种化学成分风化前后的散点图可以看出：风化后高钾类玻璃中的二氧化硅（SiO2）含量明显高于风化前二氧化硅（SiO2）含量；是否风化对高钾类玻璃中的氧化纳（Na2O）、氧化锡（SnO2）的含量无明显影响；风化后高钾类玻璃中的氧化钾（K2O）、氧化钙（CaO）、氧化镁（MgO）、氧化铝（Al203）、氧化铁（Fe203）、氧化铜（CuO）、氧化铅（PbO）、氧化钡（BaO）、五氧化二磷（P2O5）、氧化锶（SrO）、二氧化硫（SO2）的含量明显低于风化前的含量。

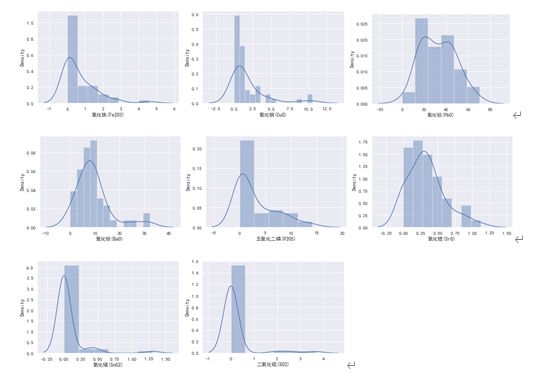
铅钡玻璃风化前后不同化学成分频率分布直方图：


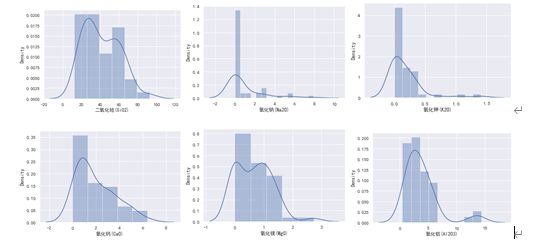
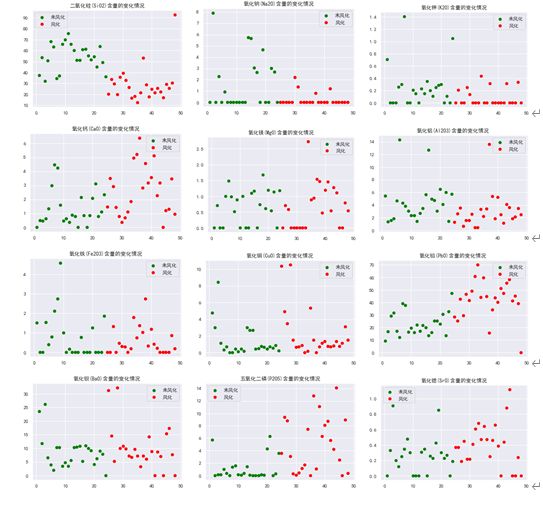
铅钡类玻璃各种化学成分风化前后的散点图：

由频率分布直方图可以直观的看出铅钡类玻璃在风化后主要化学成分含量呈上升趋势。

由高钾类玻璃各种化学成分风化前后的散点图可以看出：风化后高钾类玻璃中的氧化钙（CaO）、氧化铅（PbO）、五氧化二磷（P2O5）、氧化锶（SrO）含量明显高于风化前的含量；是否风化对铅钡类玻璃中的氧化锡（SnO2）、氧化镁（MgO）、氧化铝（Al203）、氧化铜（CuO）、氧化钡（BaO）、氧化锡（SnO2）、二氧化硫（SO2）的含量无明显影响；风化后铅钡类玻璃中的二氧化硅（SiO2）、氧化纳（Na2O）、氧化铁（Fe203）、含量明显低于风化前的含量。

3.3加权平均值占比预测模型

进一步分析，由于各个类型玻璃的化学成分含量的不同，导致可能有部分化学含量未检测到，因此数据整体上出现较多的“0”值，我们对数据进行加权求平均值处理，在权重计算部分使用标准正态分布函数进行权重的分配，计算过程如下：

那么，将每一列化学成分数据与标准正态分布函数进行相乘，其加权平均值为：


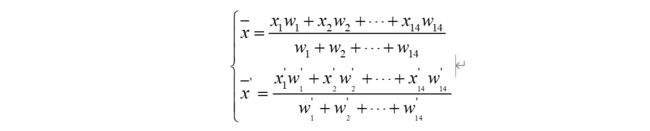
我们进行编程求解，预测出不同类型玻璃风化前化学成分含量（部分）如下表所示：