09_分类算法--k近邻算法（KNN）、案例、欧氏距离、k-近邻算法API、KNeighborsClassifier、及其里面的案例（网络资料+学习资料整理笔记）

1 分类算法–k近邻算法（KNN）

定义：如果一个样本在特征空间中**k个最相似（即特征空间中最邻近）**的样本中的大多数属于某一个类别，则该样本也属于这个类别，则该样本也属于这个类别。

k-近邻算法采用测量不同特征值之间的距离来进行分类

优点：精度高、对异常值不敏感、无数据输入假定。
缺点：计算复杂度高、空间复杂度高。
使用数据范围：数值型和标称型。

以下是《机器原理》中的关于KNN的介绍

K最近邻（k-Nearest Neighbor，KNN）分类算法可以说是最简单的机器学习算法了。它采用测量不同特征值之间的距离方法进行分类。它的思想很简单：如果一个样本在特征空间中的k个最相似（即特征空间中最邻近）的样本中的大多数属于某一个类别，则该样本也属于这个类别。

比如上面这个图，我们有两类数据，分别是蓝色方块和红色三角形，他们分布在一个上图的二维中间中。那么假如我们有一个绿色圆圈这个数据，需要判断这个数据是属于蓝色方块这一类，还是与红色三角形同类。怎么做呢？我们先把离这个绿色圆圈最近的几个点找到，因为我们觉得离绿色圆圈最近的才对它的类别有判断的帮助。那到底要用多少个来判断呢？这个个数就是k了。如果k=3，就表示我们选择离绿色圆圈最近的3个点来判断，由于红色三角形所占比例为2/3，所以我们认为绿色圆是和红色三角形同类。如果k=5，由于蓝色四方形比例为3/5，因此绿色圆被赋予蓝色四方形类。从这里可以看到，k的值还是很重要的。

该算法在分类时有个主要的不足是，当样本不平衡时，如一个类的样本容量很大，而其他类样本容量很小时，有可能导致当输入一个新样本时，该样本的K个邻居中大容量类的样本占多数。因此可以采用权值的方法（和该样本距离小的邻居权值大）来改进。该方法的另一个不足之处是计算量较大，因为对每一个待分类的文本都要计算它到全体已知样本的距离，才能求得它的K个最近邻点。目前常用的解决方法是事先对已知样本点进行剪辑，事先去除对分类作用不大的样本。该算法比较适用于样本容量比较大的类域的自动分类，而那些样本容量较小的类域采用这种算法比较容易产生误分[参考机器学习十大算法]。

总的来说就是我们已经存在了一个带标签的数据库，然后输入没有标签的新数据后，将新数据的每个特征与样本集中数据对应的特征进行比较，然后算法提取样本集中特征最相似（最近邻）的分类标签。一般来说，只选择样本数据库中前k个最相似的数据。最后，选择k个最相似数据中出现次数最多的分类。其算法描述如下：
1）计算已知类别数据集中的点与当前点之间的距离；
2）按照距离递增次序排序；
3）选取与当前点距离最小的k个点；
4）确定前k个点所在类别的出现频率；
5）返回前k个点出现频率最高的类别作为当前点的预测分类。

KNN做回归和分类的主要区别在于最后做预测时候的决策方式不同。KNN做分类预测时，一般是选择多数表决法，即训练集里和预测的样本特征最近的K个样本，预测为里面有最多类别数的类别。而KNN做回归时，一般是选择平均法，即最近的K个样本的样本输出的平均值作为回归预测值。

1.1 一个例子弄懂k-近邻

电影可以按照题材分类，每个题材又是如何定义的呢？那么假如两种类型的电影，动作片和爱情片。动作片有哪些公共的特征？那么爱情片又存在哪些明显的差别呢？我们发现动作片中打斗镜头的次数较多，而爱情片中接吻镜头相对更多。当然动作片中也有一些接吻镜头，爱情片中也会有一些打斗镜头。所以不能单纯通过是否存在打斗镜头或者接吻镜头来判断影片的类别。那么现在我们有6部影片已经明确了类别，也有打斗镜头和接吻镜头的次数，还有一部电影类型未知。

那么我们使用K-近邻算法来分类爱情片和动作片：存在一个样本数据集合，也叫训练样本集，样本个数M个，知道每一个数据特征与类别对应关系，然后存在未知类型数据集合1个，那么我们要选择一个测试样本数据中与训练样本中M个的距离，排序过后选出最近的K个，这个取值一般不大于20个。选择K个最相近数据中次数最多的分类。那么我们根据这个原则去判断未知电影的分类

我们假设K为3，那么排名前三个电影的类型都是爱情片，所以我们判定这个未知电影也是一个爱情片。那么计算距离是怎样计算的呢？

1.2 计算距离公式

两个样本的距离可以通过如下公式计算，又叫欧氏距离，比如说，a(a1,a2,a3),b(b1,b2,b3)

1.3 sklearn k-近邻算法API

参考：https://www.jianshu.com/p/871884bb4a75

sklearn.neighbors.KNeighborsClassifier(n_neighbors=5, weights=’uniform’, algorithm=’auto’, leaf_size=30, p=2, metric=’minkowski’, metric_params=None,n_jobs=None, **kwargs)[source]
     1、n_neighbors:int,可选（默认=5），k_neighbors查询默认使用的邻居数，选择最邻近的数目k。
     2、weights:邻近点的计算权重值，uniform代表各个点权重值相等。
          用于预测的权重函数。可选参数如下：
          A:‘uniform’:统一的权重. 在每一个邻居区域里的点的权重都是一样的。
          B:'distance':权重点等于他们距离的倒数。使用此函数，更近的邻居对于所预测的点的影响更大。
          C:[callable]:一个用户自定义的方法，此方法接收一个距离的数组，然后返回一个相同形状并且包含权重的数组。。
     3、algorithm：{‘auto’，‘ball_tree’，‘kd_tree’，‘brute’}，可选用于计算最近邻居的算法：‘ball_tree’将会使用 BallTree，‘kd_tree’将使用 KDTree。‘auto’将尝试根据传递给fit方法的值来决定最合适的算法。 (不同实现方式影响效率)
     4、leaf_size（叶子数量）:int,可选参数（默认为30）、
         传递给BallTree或kTree的叶子大小，这会影响构造和查询的速度，以及存储树所需的内存。
     5、p:Minkowski度量的指数参数。p = 1 代表使用曼哈顿距离 (l1)，p = 2 代表使用欧几里得距离(l2)
     6、metric：距离度量，点之间距离的计算方法。
     7、metric_params：额外的关键字度量函数。
     8、n_jobs：为邻近点搜索运行的并行作业数。

方法：

方法名	含义
fit(X,y)	使用X作为训练数据，y作为目标值（类似于标签）来拟合模型
get_params([deep])	获取估值器的参数。
kneighbors([X, n_neighbors, return_distance])	查找一个或几个点的K个邻居。返回每个点的下标和到邻居的距离。
kneighbors_graph([X,n_neighbors,mode])	计算在X数组中每个点的k邻居的（权重）图
predit(X)	给提供的数据预测对应的标签。
predict_proba(X)	返回测试数据X的概率估值。
score(X, y[, sample_weight])	返回给定测试数据和标签的平均准确值。
set_params(**params)	设置估值器的参数。

案例：

from sklearn.neighbors import KNeighborsClassifier

X = [[0],[1],[2],[3]]
y = [0,0,1,1]

neigh = KNeighborsClassifier(n_neighbors=3)
neigh.fit(X,y)

print(neigh.predict([[1.1]]))
print(neigh.predict_proba([[0.9]]))

输出结果：

[0]
[[0.66666667 0.33333333]]

fit(X,y)
使用X作为训练数据拟合模型，y作为X的类别值。X，y为数组或者矩阵

参数：
    X: {类似数组, 稀疏矩阵, BallTree, KDTree}
         待训练数据。如果是数组或者矩阵，形状为 [n_samples, n_features]，如果矩阵为’precomputed', 则形状为[n_samples, n_samples]。
    y: {类似数组, 稀疏矩阵}
         形状为[n_samples] 或者 [n_samples, n_outputs]的目标值。

案例：

import numpy as np
from sklearn.neighbors import KNeighborsClassifier

neigh = KNeighborsClassifier(n_neighbors=3)

X = np.array([[1, 1], [1, 1.1], [0, 0], [0, 0.1]])
y = np.array([1,1,0,0])

print(neigh.fit(X,y))

输出结果为：

KNeighborsClassifier(algorithm='auto', leaf_size=30, metric='minkowski',
                     metric_params=None, n_jobs=None, n_neighbors=3, p=2,
                     weights='uniform')

get_params(deep=True)
    获取估值器的参数。

参数：
    deep:boolean,可选参数
        如果为True,则返回估值器的参数，以包含子目标的估值器。
返回值：
    params:Mapping string to any
        返回Map变量，内容为[参数值:值，参数值：值，......]

kneighbors(X=None,n_neighbors=None,return_distance=True)
    查询一个或几个点的K个邻居, 返回每个点的下标和到邻居的距离。

参数：
    X: 类似数组, 形状(n_query, n_features)或者(n_query, n_indexed) 。如果矩阵是‘precomputed’，形状为(n_query, n_indexed)
         带查询的一个或几个点。如果没有提供，则返回每个有下标的点的邻居们。
    n_neighbors: int
         邻居数量 (默认为调用构造器时设定的n_neighboes的值).
    return_distance: boolean, 可选参数. 默认为 True.
         如果为 False，则不会返回距离

返回值：
    dist: array
         当return_distance =True时，返回到每个点的长度。
    ind: array
         邻居区域里最近的几个点的下标。

例子：

from sklearn.neighbors import NearestNeighbors
samples = [[0., 0., 0.], [0., .5, 0.], [1., 1., .5]]

# n_neighbors = 1故只得到1个最近的点
neigh = NearestNeighbors(n_neighbors=1)
neigh.fit(samples)
# 找到的是samples离[1.,1.,1.]最近的点，第一个值是距离值，第二个值是samples中的坐标值
print(neigh.kneighbors([[1.,1.,1.]]))
"""
输出的是：
(array([[0.5]]), array([[2]], dtype=int64))
"""

如你所见返回值为[[0.5]]和[[2]]。意思是此点是距离为0.5并且是样本中的第三个元素（下标从0开始）。你可以尝试查询多个点。

from sklearn.neighbors import NearestNeighbors
samples = [[0., 0., 0.], [0., .5, 0.], [1., 1., .5]]

# n_neighbors = 1故只得到1个最近的点
neigh = NearestNeighbors(n_neighbors=1)
neigh.fit(samples)

# 以下是查询多个点的情况
X = [[0., 1., 0.], [1., 0., 1.]]
print(neigh.kneighbors(X,return_distance=False))
"""
输出的是：
[[1]
 [2]]
"""
print(neigh.kneighbors(X,return_distance=True))
"""
输出结果：
(array([[0.5       ],
       [1.11803399]]), array([[1],
       [2]], dtype=int64))
       
其中第一个array表示分别离[0., 1., 0.]、 [1., 0., 1.]的距离
array([[1],
       [2]], dtype=int64)   表示samples的下标值
"""

kneighbors_graph(X=None,n_neighbors=None,mode=’connectivity’)
计算在X数组中每个点的k邻居的（权重）图

参数：
    X: 类似数组, 形状(n_query, n_features)。如果矩阵是‘precomputed’，形状为(n_query, n_indexed)
       一个或多个待查询点。如果没有提供，则返回每个有下标的点的邻居们。
    n_neighbors: int
       邻居数量。(默认为调用构造器时设定的n_neighboes的值)。
    mode: {‘connectivity’, ‘distance’}, 可选参数
       返回矩阵数据类型： ‘connectivity’ 会返回1和0组成的矩阵。 in ‘distance’ 会返回点之间的欧几里得距离。
   
    A:CSR格式的稀疏矩阵，形状为 [n_samples, n_samples_fit]
       n_samples_fit 是拟合过的数据中样例的数量，其中 A[i, j] 代表i到j的边的权重。

例子：

from sklearn.neighbors import NearestNeighbors
neigh = NearestNeighbors(n_neighbors=2)
X=[[0],[3],[1]]
neigh.fit(X)
A = neigh.kneighbors_graph(X)
print(A.toarray())

输出结果：

[[1. 0. 1.]
 [0. 1. 1.]
 [1. 0. 1.]]

predict(X)
给提供的数据预测相应的类别标签

参数：
    X:类似数组, 形状(n_query, n_features)。 如果矩阵是‘precomputed’，形状为(n_query, n_indexed)待测试样例。
返回值：
    y: 形状为 [n_samples] 或者 [n_samples, n_outputs]的数组
    返回每个待测试样例的类别标签。

predict_proba(X)
返回测试数据X的概率估值。

参数：
    X:类似数组, 形状(n_query, n_features)。 如果矩阵是‘precomputed’，形状为(n_query, n_indexed) 的待测样例。
返回值：
    p:形状为[n_samples,n_classes]的数组，或者是n_outputs列表。
    输入样例的类别概率估值。其中类别根据词典顺序排序。

score(X,y,sample_weight=None)
返回给定测试数据和标签的平均准确度。在多标签分类中，返回的是各个子集的准确度。

参数：
    X:类似数组，形状为（n_samples,n_features）待测试样例。
 
    y:类似数组，形状为（n_samples）或者（n_samples,n_outputs）
        X对于的正确标签

    sample_weight:类似数组，形状为[n_samples],可选参数。待测试的权重。

返回值：
    score:float
         self.predict(X)关于y的平均准确率。

set_params(**params)
设置估值器的参数。

此方法在单个估值器和嵌套对象（例如管道）中有效。

返回值:
              self

使用到sklearn.neighbors.KNeighborsClassifier的案例
Classifier comparison ： https://scikit-learn.org/stable/auto_examples/classification/plot_classifier_comparison.html#sphx-glr-auto-examples-classification-plot-classifier-comparison-py

Plot the decision boundaries of a VotingClassifier：https://scikit-learn.org/stable/auto_examples/ensemble/plot_voting_decision_regions.html#sphx-glr-auto-examples-ensemble-plot-voting-decision-regions-py

Digits Classification Exercise ： https://scikit-learn.org/stable/auto_examples/exercises/plot_digits_classification_exercise.html#sphx-glr-auto-examples-exercises-plot-digits-classification-exercise-py

Nearest Neighbors Classification: https://scikit-learn.org/stable/auto_examples/neighbors/plot_classification.html#sphx-glr-auto-examples-neighbors-plot-classification-py

1.4 k-近邻算法案例分析

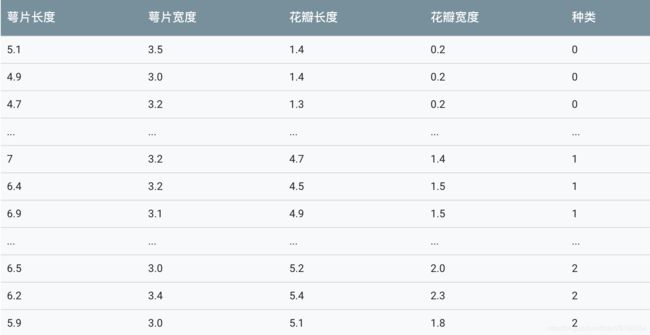
本案例使用最著名的"鸢尾"数据集，该数据集曾经被Fisher用在经典论文中，目前作为教科书般的数据样本预存在Scikit-learn的工具包中。

from sklearn.datasets import load_iris
#使用加载器读取数据并存入变量iris
iris = load_iris()

#查验数据规模
print(iris.data.shape)

#查看数据说明（这是一个好习惯）
print(iris.DESCR)

通过上述代码对数据的查验以及数据本身的描述，我们了解到Iris数据集共有150朵鸢尾数据样本，并且均匀分布在3个不同的亚种；每个数据样本有总共4个不同的关于花瓣、花萼的形状特征所描述。由于没有制定的测试集合，因此按照惯例，我们需要对数据进行随即分割，25%的样本用于测试，其余75%的样本用于模型的训练。

由于不清楚数据集的排列是否随机，可能会有按照类别去进行依次排列，这样训练样本的不均衡的，所以我们需要分割数据，已经默认有随机采样的功能。

对Iris数据集进行分割

# 用于获取鸢尾花的数据集
from sklearn.datasets import load_iris
#数据切分
from sklearn.model_selection import train_test_split
# 标准化的库
from sklearn.preprocessing import StandardScaler

#使用加载器读取数据并存入变量iris
iris = load_iris()

#查验数据规模
print(iris.data.shape)

#查看数据说明（这是一个好习惯）
print(iris.DESCR)

# 对iris数据集进行分割
X_train,X_test,y_train,y_test = train_test_split(iris.data,iris.target,test_size=0.25,random_state=42)

# 对特征数据进行标准化
ss = StandardScaler()
X_train = ss.fit_transform(X_train)
X_test = ss.fit_transform(X_test)

K近邻算法是非常直观的机器学习模型，我们可以发现K近邻算法没有参数训练过程，也就是说，我们没有通过任何学习算法分析训练数据，而只是根据测试样本训练数据的分布直接作出分类决策。因此，K近邻属于无参数模型中非常简单一种。

# 用于获取鸢尾花的数据集
from sklearn.datasets import load_iris
#数据切分
from sklearn.model_selection import train_test_split
# 标准化的库
from sklearn.preprocessing import StandardScaler
# K近邻算法
from sklearn.neighbors import KNeighborsClassifier
from sklearn.metrics import classification_report
from sklearn.model_selection import GridSearchCV

def knniris():
    """
    鸢尾花分类
    :return: None
    """

    # 1、数据集获取和分割
    lr = load_iris()

    x_train, x_test, y_train, y_test = train_test_split(lr.data, lr.target, test_size=0.25)

    # 2、进行标准化

    std = StandardScaler()

    x_train = std.fit_transform(x_train)
    x_test = std.transform(x_test)

    # 3、estimator流程
    knn = KNeighborsClassifier()

    # 4、得出模型
    knn.fit(x_train,y_train)

    # 5、进行预测或得出精度(得出x_test所属的分类)
    y_predict = knn.predict(x_test)
    print(y_predict)
    """
    结果：[1 0 1 2 2 2 2 2 0 1 1 0 0 2 2 0 1 2 2 1 2 2 1 0 1 0 0 0 2 1 1 2 0 2 0 0 2 2]
    """

    score = knn.score(x_test,y_test)
    print(score)
    """
    结果为：0.9473684210526315
    """

    #===============================================================
    print("===============================================================")
    # 通过网格搜索,n_neighbors为参数列表
    param = {"n_neighbors": [3, 5, 7]}

    gs = GridSearchCV(knn, param_grid=param, cv=10)

    # 建立模型
    gs.fit(x_train, y_train)

    # print(gs)

    # 预测数据

    print(gs.score(x_test, y_test))

    # 分类模型的精确率和召回率

    # print("每个类别的精确率与召回率：",classification_report(y_test, y_predict,target_names=lr.target_names))

    return None

if __name__ == "__main__":
    knniris()

输出结果：

[1 0 0 1 2 2 1 0 0 1 1 1 0 1 2 0 1 2 1 1 0 2 2 1 0 0 0 0 0 2 2 0 2 1 2 1 1 2]
0.9736842105263158
===============================================================
D:\installed\Anaconda3\lib\site-packages\sklearn\model_selection\_search.py:814: DeprecationWarning: The default of the `iid` parameter will change from True to False in version 0.22 and will be removed in 0.24. This will change numeric results when test-set sizes are unequal.
  DeprecationWarning)
0.9736842105263158

案例2：Facebook-K-近邻预测用户签到位置案例


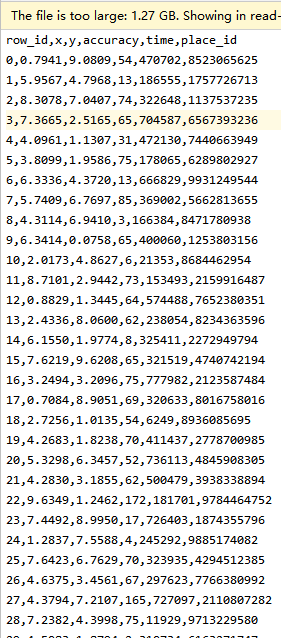
数据格式：

from sklearn.model_selection import train_test_split, GridSearchCV
from sklearn.neighbors import KNeighborsClassifier
from sklearn.preprocessing import StandardScaler
import pandas as pd

def knncls():
    """
    K-近邻预测用户签到位置
    :return:None
    """
    # 读取数据
    data = pd.read_csv("train.csv")

    # print(data.head(10))

    # 处理数据
    # 1、缩小数据,查询数据晒讯
    data = data.query("x > 1.0 &  x < 1.25 & y > 2.5 & y < 2.75")

    # 处理时间的数据
    time_value = pd.to_datetime(data['time'], unit='s')

    print(time_value)

    # 把日期格式转换成 字典格式
    time_value = pd.DatetimeIndex(time_value)

    # 构造一些特征
    data['day'] = time_value.day
    data['hour'] = time_value.hour
    data['weekday'] = time_value.weekday

    # 把时间戳特征删除
    data = data.drop(['time'], axis=1)

    print(data)

    # 把签到数量少于n个目标位置删除
    place_count = data.groupby('place_id').count()

    tf = place_count[place_count.row_id > 3].reset_index()

    data = data[data['place_id'].isin(tf.place_id)]

    # 取出数据当中的特征值和目标值
    y = data['place_id']

    x = data.drop(['place_id'], axis=1)

    # 进行数据的分割训练集合测试集
    x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.25)

    # 特征工程（标准化）
    std = StandardScaler()

    # 对测试集和训练集的特征值进行标准化
    x_train = std.fit_transform(x_train)

    x_test = std.transform(x_test)

    # 进行算法流程 # 超参数
    knn = KNeighborsClassifier()

    # # fit， predict,score
    # knn.fit(x_train, y_train)
    #
    # # 得出预测结果
    # y_predict = knn.predict(x_test)
    #
    # print("预测的目标签到位置为：", y_predict)
    #
    # # 得出准确率
    # print("预测的准确率:", knn.score(x_test, y_test))

    # 构造一些参数的值进行搜索
    param = {"n_neighbors": [3, 5, 10]}

    # 进行网格搜索
    gc = GridSearchCV(knn, param_grid=param, cv=2)

    gc.fit(x_train, y_train)

    # 预测准确率
    print("在测试集上准确率：", gc.score(x_test, y_test))
    print("在交叉验证当中最好的结果：", gc.best_score_)
    print("选择最好的模型是：", gc.best_estimator_)
    print("每个超参数每次交叉验证的结果：", gc.cv_results_)

    return None


if __name__ == "__main__":
    knncls()

输出结果为：

600        1970-01-01 18:09:40
957        1970-01-10 02:11:10
4345       1970-01-05 15:08:02
4735       1970-01-06 23:03:03
5580       1970-01-09 11:26:50
                   ...        
29100203   1970-01-01 10:33:56
29108443   1970-01-07 23:22:04
29109993   1970-01-08 15:03:14
29111539   1970-01-04 00:53:41
29112154   1970-01-08 23:01:07
Name: time, Length: 17710, dtype: datetime64[ns]
E:/workspace/numpy/sklearn/03_KNeighborsClassifier.py:165: SettingWithCopyWarning: 
A value is trying to be set on a copy of a slice from a DataFrame.
Try using .loc[row_indexer,col_indexer] = value instead
See the caveats in the documentation: http://pandas.pydata.org/pandas-docs/stable/user_guide/indexing.html#returning-a-view-versus-a-copy
  data['day'] = time_value.day
E:/workspace/numpy/sklearn/03_KNeighborsClassifier.py:166: SettingWithCopyWarning: 
A value is trying to be set on a copy of a slice from a DataFrame.
Try using .loc[row_indexer,col_indexer] = value instead
See the caveats in the documentation: http://pandas.pydata.org/pandas-docs/stable/user_guide/indexing.html#returning-a-view-versus-a-copy
  data['hour'] = time_value.hour
E:/workspace/numpy/sklearn/03_KNeighborsClassifier.py:167: SettingWithCopyWarning: 
A value is trying to be set on a copy of a slice from a DataFrame.
Try using .loc[row_indexer,col_indexer] = value instead
See the caveats in the documentation: http://pandas.pydata.org/pandas-docs/stable/user_guide/indexing.html#returning-a-view-versus-a-copy
  data['weekday'] = time_value.weekday
            row_id       x       y  accuracy    place_id  day  hour  weekday
600            600  1.2214  2.7023        17  6683426742    1    18        3
957            957  1.1832  2.6891        58  6683426742   10     2        5
4345          4345  1.1935  2.6550        11  6889790653    5    15        0
4735          4735  1.1452  2.6074        49  6822359752    6    23        1
5580          5580  1.0089  2.7287        19  1527921905    9    11        4
            ...     ...     ...       ...         ...  ...   ...      ...
29100203  29100203  1.0129  2.6775        12  3312463746    1    10        3
29108443  29108443  1.1474  2.6840        36  3533177779    7    23        2
29109993  29109993  1.0240  2.7238        62  6424972551    8    15        3
29111539  29111539  1.2032  2.6796        87  3533177779    4     0        6
29112154  29112154  1.1070  2.5419       178  4932578245    8    23        3
[17710 rows x 8 columns]
D:\installed\Anaconda3\lib\site-packages\sklearn\model_selection\_split.py:657: Warning: The least populated class in y has only 1 members, which is too few. The minimum number of members in any class cannot be less than n_splits=2.
  % (min_groups, self.n_splits)), Warning)
在测试集上准确率： 0.4189125295508274
在交叉验证当中最好的结果： 0.39344262295081966
选择最好的模型是： KNeighborsClassifier(algorithm='auto', leaf_size=30, metric='minkowski',
                     metric_params=None, n_jobs=None, n_neighbors=10, p=2,
                     weights='uniform')
每个超参数每次交叉验证的结果： {'mean_fit_time': array([0.01545823, 0.00547051, 0.00598311]), 'std_fit_time': array([1.04693174e-02, 4.82320786e-04, 2.78949738e-05]), 'mean_score_time': array([0.36103368, 0.38176703, 0.47072983]), 'std_score_time': array([0.02695775, 0.01324654, 0.02192879]), 'param_n_neighbors': masked_array(data=[3, 5, 10],
             mask=[False, False, False],
       fill_value='?',
            dtype=object), 'params': [{'n_neighbors': 3}, {'n_neighbors': 5}, {'n_neighbors': 10}], 'split0_test_score': array([0.34967218, 0.37308773, 0.39541055]), 'split1_test_score': array([0.35561923, 0.37695002, 0.39143585]), 'mean_test_score': array([0.35261665, 0.375     , 0.39344262]), 'std_test_score': array([0.00297338, 0.00193105, 0.00198726]), 'rank_test_score': array([3, 2, 1])}

1.5 实例流程

1、数据集的处理
2、分割数据集
3、对数据集进行标准化
4、estimator流程进行分类预测

1.6 问题

1、k值取多大？有什么影响
k值取很小：容易受异常点影响
k值取很大：容易受最近数据太多导致比例变化

1.7 k-近邻算法优缺点

1、优点
    1.1 简单，易于理解，易于实现，无需估计参数，无需训练
2、缺点
    2.1 懒惰算法，对测试样本分类时的计算量大，内存开销大。
    2.2 必须指定K值，K值选择不当则分类精度不能保证
3、使用场景：小数据场景，几千～几万样本，具体场景具体业务去测试

1.8 k-近邻算法实现

加快搜索速度——基于算法的改进KDTree,API接口里面有实现。

1.9 k近邻算法作业：

1、通过k-近邻算法对生物物种进行分类——鸢尾花(load_iris)