使用python搭建单隐藏层神经网络用于分类

一、工作介绍

1.搭建的神经网络类型：

本文搭建的神经网络为二层神经网络结构（输入层是已知的，不算做层数），即一个输入层+一个隐藏层+一个输出层。

二、神经网络搭建流程

1. 设置神经网络结构

• 输入层节点数取决于特征数
• 隐藏层节点数需要自己给定
• 输出层节点数取决于分类的类别数（二元分类输出层节点数为1 ）

2. 随机初始化权重

3. 梯度下降迭代过程

• 前向传播
• 计算代价
• 反向传播
• 更新参数

三、实验

1. 数据

数据集大家根据需要选择，可以选择开放数据集。我选择的数据集是乳腺癌肿瘤数据集，有需要的可自行下载。
友情提示： 此数据集的标签 y 取值分别为2和4，大家在程序中需要改为0和1，不然会出错。

2. 各步骤具体实现过程

（1）梯度下降迭代过程

'''
构建神经网络模型
'''
def nn_model(X, Y, n_h, epoch = 10000):
    X.astype(np.double)
    #随机初始化参数
    np.random.seed(3)
    n_x = X.shape[1]         # 特征数 , 9
    n_y = Y.shape[0]         # 标签值 , 1
    paras = random_init_para(n_x, n_h, n_y)

    for i in range(0, epoch):
        # 前向传播
        A2, cache = forward_propagation(X, paras)
        # 计算代价cost
        cost = compute_cost(Y, A2)
        # 反向传播
        grads = back_propagation(X, Y, paras, cache)
        # 梯度下降参数更新
        paras = update_parameters(paras, grads)
        if i % 1000 == 0:
            print("Cost after iteration %i: %f" % (i, cost))
            # print(grads)
            # print(paras)

    return paras

（2）前向传播过程

'''
前向传播
'''
def forward_propagation(X, paras):

    W1 = paras["W1"]              # (n_h, n_x) = (5, 9)
    b1 = paras["b1"]              # (n_h, 1) = (5, 1)
    W2 = paras["W2"]              # (n_y, n_h) = (1, 5)
    b2 = paras["b2"]              # (n_y, 1) = (1, 1)

    Z1 = np.dot(W1, X.T.astype(np.double)) + b1         # (n_h, 样本数) = (5,511)
    A1 = np.tanh(Z1.astype(np.double))                  #
    Z2 = np.dot(W2, A1) + b2          # (n_y, 样本数) = (1, 511)
    A2 = sigmoid(Z2)

    cache = {
        "Z1": Z1,
        "A1": A1,
        "Z2": Z2,
        "A2": A2
    }

    return A2, cache

（3）计算代价cost

'''
计算损失
'''
def compute_cost(Y, A2):

    m = Y.shape[1]     # m表示数据集大小
    logpropa = Y * np.log(A2) + (1 - Y) * np.log(1 - A2)
    cost = - np.sum(logpropa)/m
    cost = np.squeeze(cost)     # makes sure cost is the dimension we expect.
                                # E.g., turns [[17]] into 17
    cost = float(cost)          # without it, type error
    assert (isinstance(cost, float))
    return float(cost)

（4）反向传播过程

'''
反向传播
'''
def back_propagation(X, Y, paras, cache):
    # X = X.astype(np.float64)  # 将矩阵X中的元素全都转成float型
    m = X.shape[0]                                        # 样本数量
    W1 = paras["W1"]
    b1 = paras["b1"]
    W2 = paras["W2"]                                      # (n_y, n_h) = (1, 5)
    b2 = paras["b2"]
    A1 = cache["A1"]
    A2 = cache["A2"]
    dZ2 = A2 - Y                                          # (1，样本数)
    dW2 = (1/m) * (np.dot(dZ2, A1.T))                     # (1, n_h) = (1, 5)
    db2 = (1/m) * np.sum(dZ2, axis=1, keepdims=True)      #
    dZ1 = np.dot(W2.T, dZ2) * (1 - np.power(A1, 2))       # (n_h, 样本数) = (5, 样本数)
    dW1 = (1/m) * (np.dot(dZ1, X.astype(np.double)))      # (n_h, n_x) = (5, 9), 刚好等于W的维度
    db1 = (1/m) * np.sum(dZ1, axis=1, keepdims=True)

    grads = {
        "dW1": dW1,
        "db1": db1,
        "dW2": dW2,
        "db2": db2
    }

    return  grads

（5）参数更新过程

'''
更新参数
'''
def update_parameters(paras, grads, learn_rate = 1.2):
    W1 = paras["W1"]
    b1 = paras["b1"]
    W2 = paras["W2"]
    b2 = paras["b2"]
    dW1 = grads["dW1"]
    db1 = grads["db1"]
    dW2 = grads["dW2"]
    db2 = grads["db2"]
    W1 = W1 - learn_rate * dW1
    b1 = b1 - learn_rate * db1
    W2 = W2 - learn_rate * dW2
    b2 = b2 - learn_rate * db2

    paras = {
        "W1": W1,
        "b1": b1,
        "W2": W2,
        "b2": b2
    }

    return paras

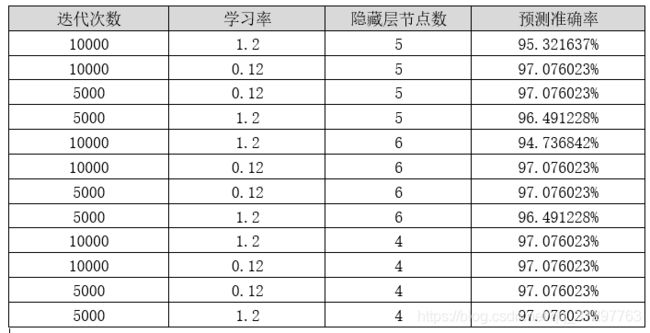
四、分析与总结

1. 迭代5000次和10000次的准确率一样，说明5000次的时候，基本已经达到代价最低了
2. 对于此数据集，隐藏层节点数为4的时候效果更好。

以上仅代表个人见解，如有错误或侵权请给作者留言。