数据压缩读书笔记——线性代数的几何意义（三）

第二章 向量的基本几何意义

2.1 向量概念的几何意义

自由向量的概念

   向量（vector）是一个既有大小又有方向的量。这个量本身就是个几何的概念。
  在一条直线上平移的向量称为自由向量（物理学中常称为滑动向量）。

  凡是两个向量大小相等、方向相同的，我们就说这两个向量是相等的。

向量的数学表示

  在数学学科中，向量被处理为自由向量，为了与解析技术所用的坐标联系起来，我们把空间中所有的向量的尾部都拉到坐标原点，这样$N$维点空间可以与$N$维向量空间建立一一对应关系；$N$维点空间中点$(0,0,\cdots ,0)$取做原点，那么每一个点都可以让一个向量和它对应，这个向量就是从坐标原点出发到这个点为止的向量。
  虽然$N$维向量的几何意义难以想象，但其现实意义我们还是可以把握的。比如，在三维空间中，我们只要知道一个球的球心的位置和半径的大小就可以确定这个球面。把球心坐标和半径值写成有序数组，我们就得到了一个四维向量。
  一个三维向量可以分解为三个单位坐标向量的线性表示：
$$(1,1,1)=(1,0,0)+(0,1,0)+(0,0,1)=\stackrel{\rightharpoonup }{i}+\stackrel{\rightharpoonup }{j}+\stackrel{\rightharpoonup }{k}$$
  把单位坐标向量$\stackrel{\rightharpoonup }{i}$，$\stackrel{\rightharpoonup }{j}$，$\stackrel{\rightharpoonup }{k}$分别首尾连接相加，就得到了$(1,1,1)$的图像。
  向量的运算有加法、减法和乘法三种，没有处罚。

2.2 向量的加法的几何及物理意义

  即平行四边形法则。

2.3 向量的内积的几何及物理意义

  向量的内积也叫数量积、标积、点积，内积的结果是个数量或者标量。
  内积的定义有两个。
$$\stackrel{\rightharpoonup }{a}\cdot \stackrel{\rightharpoonup }{b}=abcos\theta$$$$\stackrel{\rightharpoonup }{a}\cdot \stackrel{\rightharpoonup }{b}=a_x{b}_x+a_y{b}_y+a_z{b}_z$$
  向量内积的几何解释就是一个向量在另一个向量上的投影的积，也就是同方向的积。
  特别的，如果一个向量如$\stackrel{\rightharpoonup }{a}$是某个坐标轴的单位坐标向量，那么，两个向量的内积$\stackrel{\rightharpoonup }{a}\cdot \stackrel{\rightharpoonup }{b}$就是向量$\stackrel{\rightharpoonup }{b}$在此坐标轴上的坐标值，这是傅里叶分析的理论基础。

向量的内积与正交变换

  定理1：设$\sigma$是$V$（欧式空间）的一个变换。若对任意向量$\stackrel{\rightharpoonup }{a},\stackrel{\rightharpoonup }{b}\in V$，都有$$|\sigma (\stackrel{\rightharpoonup }{a})+\sigma (\stackrel{\rightharpoonup }{b})|=|\stackrel{\rightharpoonup }{a}+\stackrel{\rightharpoonup }{b}|$$
  则$\sigma$是$V$的一个正交变换。

定理的几何意义是：保持以$V$中任意两个向量为邻边的平行四边形的对角线之长不变

  定理2：设$\sigma$是$V$的一个变换，如果$\sigma$既是保长度变换又是保夹角变换，那么$\sigma$必为正交变换。

2.4 向量的外积的几何和物理意义

叉积的定义和几何解释

  向量的外积也译作叉积。叉积会产生新维度。两个向量确定了一个二维的平面，叉积又会产生垂直于这个平面的向量，因此，叉积的概念只能应用于3维及3维以上的向量空间。
  叉积的定义有两个：$$\stackrel{\rightharpoonup }{a}\times \stackrel{\rightharpoonup }{b}=(a_y{b}_z-a_z{b}_y,a_z{b}_x-a_x{b}_z,a_x{b}_y-a_y{b}_x)$$$$\stackrel{\rightharpoonup }{a}\times \stackrel{\rightharpoonup }{b}=absin\theta N(其中N是垂直于\stackrel{\rightharpoonup }{a}和\stackrel{\rightharpoonup }{b}展成的平面的单位向量$$

叉积的物理意义

  叉积向量在物理学中又被称为赝向量或轴向量。物理上有着众多应用。

2.5 向量混合运算的几何意义

向量叉积的分配律的几何解释1

  向量分配律：$$(\stackrel{\rightharpoonup }{a}+\stackrel{\rightharpoonup }{b})\times \stackrel{\rightharpoonup }{c}=\stackrel{\rightharpoonup }{a}\times \stackrel{\rightharpoonup }{c}+\stackrel{\rightharpoonup }{b}\times \stackrel{\rightharpoonup }{c}$$

  一投一转，再加一伸

向量叉积的分配律的几何解释2

有向面积：有向线段被用来作为向量的图形。那么面积也是有方向的。在微积分对$x-y$平面上的曲线与$x$坐标轴围成的面积积分中，$x$坐标轴上方的面积积分值为正，轴下方的面积积分值为负。这实际上也是面积有方向的表现。

  向量不但可以表示一个有方向的线段，而且也可以表示一个有方向的面积。反过来讲，一个有向线段（一定长度的箭头）被用来作为向量的几何图形（这是几乎所有数学书的做法），而一个有方向的面积也可以表示一个向量。为了方便，称前者为线向量，称后者为面向量。
  面向量的加法运算同样满足平行四边形法则和三角形法则。

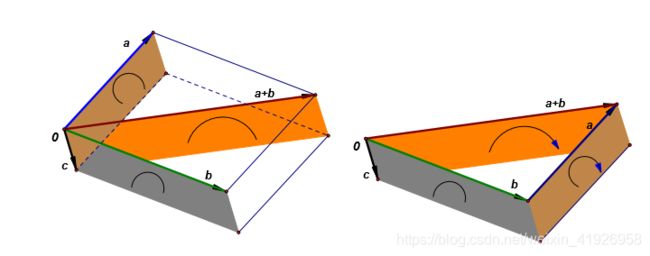
向量混合积的几何解释

1. $(\stackrel{\rightharpoonup }{a}\times \stackrel{\rightharpoonup }{b})\cdot \stackrel{\rightharpoonup }{c}$叫做三向量的混合积或三重数积。
2. $(\stackrel{\rightharpoonup }{a}\times \stackrel{\rightharpoonup }{b})\times \stackrel{\rightharpoonup }{c}$叫做三重矢积。

  三向量的混合积有关系：$(\stackrel{\rightharpoonup }{a}\times \stackrel{\rightharpoonup }{b})\cdot \stackrel{\rightharpoonup }{c}=(\stackrel{\rightharpoonup }{b}\times \stackrel{\rightharpoonup }{c})\cdot \stackrel{\rightharpoonup }{a}=(\stackrel{\rightharpoonup }{c}\times \stackrel{\rightharpoonup }{a})\cdot \stackrel{\rightharpoonup }{b}$
  混合积的绝对值表示以向量$\stackrel{\rightharpoonup }{a},\stackrel{\rightharpoonup }{b},\stackrel{\rightharpoonup }{c}$为棱的平行六面体的体积。如果向量$\stackrel{\rightharpoonup }{a},\stackrel{\rightharpoonup }{b},\stackrel{\rightharpoonup }{c}$以顺序组成右手系，那么积的符号是正的；如果组成左手系，积就是负的。

2.6 向量的积和张量之间关系

二维向量的内积、外积和张量

  $\stackrel{\rightharpoonup }{a}\stackrel{\rightharpoonup }{b}=a_x{b}_x\stackrel{\rightharpoonup }{i}\stackrel{\rightharpoonup }{i}+a_y{b}_y\stackrel{\rightharpoonup }{j}\stackrel{\rightharpoonup }{j}+(a_x{b}_y\stackrel{\rightharpoonup }{i}\stackrel{\rightharpoonup }{j}+a_y{b}_x\stackrel{\rightharpoonup }{j}\stackrel{\rightharpoonup }{i}）$的第一部分包含了向量$\stackrel{\rightharpoonup }{a}$和$\stackrel{\rightharpoonup }{b}$内积的结果，第二部分包含了向量$\stackrel{\rightharpoonup }{a}$和$\stackrel{\rightharpoonup }{b}$外积结果或者是行列式的结果。
  综上：向量的内积运算、外积运算覆盖了二维向量及其复数的所有乘积模式的结果。向量的张量积包含了向量的内积和外积的结果。$$\stackrel{\rightharpoonup }{a}\stackrel{\rightharpoonup }{b}=(\stackrel{\rightharpoonup }{a}\cdot \stackrel{\rightharpoonup }{b})+(\stackrel{\rightharpoonup }{a}\times \stackrel{\rightharpoonup }{b})$$

三维向量的内积、外积和张量

  分析方法同二维向量。

2.7 向量有没有除法？

1. 点积没有除法
2. 叉积也没有除法
3. 联立方程$$\{\begin{array}{l}\stackrel{\rightharpoonup }{a}\cdot \stackrel{\rightharpoonup }{b}=c\\ \stackrel{\rightharpoonup }{a}\times \stackrel{\rightharpoonup }{b}=\stackrel{\rightharpoonup }{c}\end{array}$$整理得到，$$\stackrel{\rightharpoonup }{b}=\frac{c\stackrel{\rightharpoonup }{a}-\stackrel{\rightharpoonup }{a}\times \stackrel{\rightharpoonup }{c}}{\stackrel{\rightharpoonup }{a}\cdot \stackrel{\rightharpoonup }{a}}$$这就是向量的除法。

2.8 向量的投影和几何解释

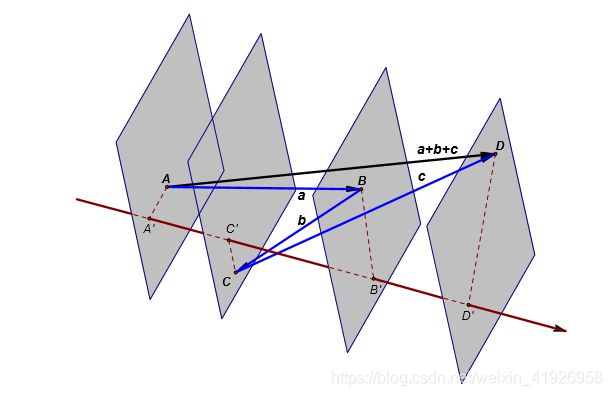
多个向量在任意轴上的投影和

  向量加法的推广之一就是：
  多个或有限个向量的和在任意轴上投影等于各个向量在同一轴上投影的和。

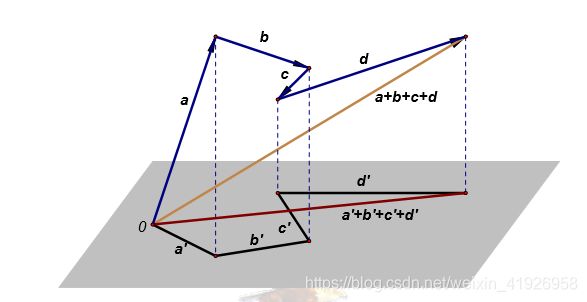
多个向量在任意平面上的投影和

  向量加法的推广之二就是：
  多个或有限个向量的和在任意平面上投影等于各个向量在同一平面上投影的和。

2.9 变向量的几何意义

变向量的应用

  变向量简化了线性方程或方程组，但这种简化与线性方程组的向量方程或者矩阵方程对线性方程的简化又有所不同。
  对于二阶线性方程组$$\{\begin{array}{l}{x}_2=a_1{x}_1+b_1\\ x_2=a_2{x}_1+b_2\end{array}$$
  可以用变向量的交$(x_1,a_1{x}_1+b_1)\bigcap (x_1,a_2{x}_1+b_2)$来等价表示。可以想象，两个变向量相同的向量就是他们的交集。如果两个向量相同，那么向量的夹角就会为0，根据行列式的几何意义知道，两个夹角为零的向量构成的平行四边形为零。

行列式的几何意义一般有两个解释

1. 行列式中的行或列向量所构成的超平行多面体的有向面积或有向体积。
2. 矩阵A的行列式就是线性变换A下的图形面积或体积的伸缩因子。

  可得公式：$$\left|\begin{array}{cc}{x}_1& a_1{x}_1+b_1\\ x_1& a_2{x}_1+b_2\end{array}\right|=0$$
  化简整理得到$x_1=0$或者$x_1=\frac{b_1-b_2}{a_2-a_1}$。进而得到向量对$(0,b_1),(0,b_2)$和$(\frac{b_1-b_2}{a_2-a_1},\frac{a_2{b}_1-a_1{b}_2}{a_2-a_1})$。
  实际上，应用行列式可以求出所有的相关向量。如上式得到了两对线性相关的向量。其中一对向量重合，即得到了线性方程组的解$(\frac{b_1-b_2}{a_2-a_1},\frac{a_2{b}_1-a_1{b}_2}{a_2-a_1})$

这块不太懂

2.10 向量的“社会关系”

向量和矢量

  向量就是矢量

向量与数

  复数为“媒”，撑起“向量空间”一片天史载。进入19世纪，“复数”充当了催化剂，复数的几何表示被提出来，高斯建立了复平面的概念，从而使向量与复数建立起一一对应的关系。这不但为虚数的现实化提供了可能，也为向量的发展开辟了道路。令人失望的是，哈密发现，要形成有加减乘除四则运算的数系，只能是四元数，而且不得不放弃乘法的交换律。最后发现的八元数，连结合律也维持不了。除此以外，其他维数的向量，根本无法定义四则运算，谈不上构成数系。

向量和三角

  三角是联系几何和代数的一座桥梁，数形结合的一份经典，沟通初等数学和高等数学的一条通道。

相关文章

数据压缩读书笔记——线性代数的几何意义（一）
数据压缩读书笔记——线性代数的几何意义（二）
数据压缩读书笔记——线性代数的几何意义（四）
数据压缩读书笔记——线性代数的几何意义（五）
数据压缩读书笔记——线性代数的几何意义（六）