灰色预测模型matlab_灰色预测
你好，我是goldsunC
让我们一起进步吧！
文章目录
灰色预测引言灰色预测的类型最简单的模型：GM(1，1)GM(1，1)模型实例原理及求解数据处理方法：1.累加生成2.累减生成3.均值生成求解步骤框图求解步骤小误差概率p及方差比检验标准(可在题目无要求精度时相对比较)The End : MATLAB求解代码
灰色预测
引言
古人说：“凡事预则立，不预则废。”办任何事情之前，必须先调查研究，摸清情况，深思熟虑，有科学的预见，周密的计划，这样才能达到预期的成功。
所谓预测，就是人们根据可获得的历史和现实数据，资料，运用一定的科学方法和手段，对人类社会、政治、军事、科学技术等发展趋势作出科学推测，以指导未来行动的方向，减少处理未来事件的盲目性。
灰色预测基于人们对系统演化不确定性特征的认识，运用序列算子对原始数据进行生成、处理，挖掘系统演化规律，建立灰色系统模型，对系统的未来状态作出科学的定量预测。同时，对于一个具体问题，究竟应该选择什么样的预测模型，应以充分的定性分析结论作为依据。模型的选择不是一成不变的，一个模型要经过多种检验才能判定其是否合理，是否有效。只有通过检验的模型才能用作预测模型。
灰色预测的类型
时间序列预测
灾变预测
波形预测
系统预测
本篇文章例子为时间序列预测，其他类型使用方面较少并且比较深入，大家可以去借鉴别人文章。
最简单的模型：GM(1，1)
GM(1，1)模型
G：Grey(灰色)；M：模型；(1,1)：只含有一个变量的一阶微分方程模型；
实例
| 年份 | 1995 | 1996 | 1997 | 1998 | 1999 | 2000 | 2001 | 2002 | 2003 | 2004 |
|---|---|---|---|---|---|---|---|---|---|---|
| 污水/亿吨 | 174 | 179 | 183 | 189 | 207 | 234 | 220.5 | 256 | 270 | 285 |
题目要求：根据给定表中数据预测未来10年的长江污水量
原理及求解
数据处理方法：
1.累加生成
原始序列为X(x=1 2 3…)
生成序列为Y(y=1 2 3…)
则：
Y(1)=X(1)
Y(2)=Y(1)+X(2)
Y(3)=Y(2)+X(3)
…
所谓的累加生成，就是将同一序列中的数据逐次相加以生成新的数据的一种手段，累加前的数列成为原始数列。累加后的数列称为原始数列。累加后的数列成为生成数列。累加生成是使灰色系统变白的一种方法，它在灰色系统理论中占有极其重要的地位。通过累加生成可以看出灰量累积过程的发展态势，使杂乱无章的原始数据中蕴含的积分特性或规律加以显化。
2.累减生成
原始序列为X(x=1 2 3…)
生成序列为Y(y=1 2 3…)
则：
Y(1)=X(1)
Y(2)=X(2)-X(1)
Y(3)=X(3)-X(2)
…
累减生成是在获取增量信息时常用的生成，多数情况下累减生成对累加生成起还原作用，即累减生成是累加生成的逆运算。
3.均值生成
原始序列为X(x=1 2 3…)
生成序列为Y(y=1 2 3…)
Y(1)=X(1)
Y(2)=aX(2)+(1-a)X(1)
Y(3)=aX(3)+(1-a)X(2)
…
在收集数据的时候，由于一些不易克服的困难导致数据序列出现空缺或无法使用的异常数据，需要在数据预处理中解决。均值生成是常用的构造新数据、填补老数据空穴、生成新数列的方法。
求解步骤框图
流程图：
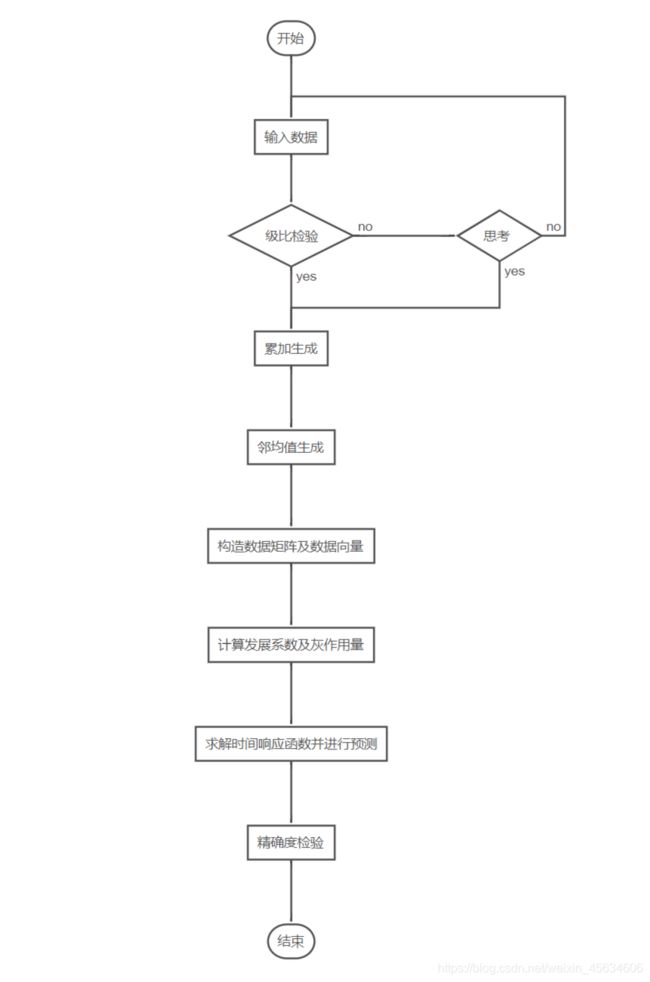
求解步骤
Step1：
首先建立时间序列如下:
X=(x(1),x(2),…x(n))
求级比L(k)：
L(k)=x(k-1)/x(k)
当所有的L(k)落在【exp(-2/(n+1)),exp(2/(n+1))】区间之内,认为可以做比较满意的GM(1,1)建模。(并不是说有的数据没落入区间之内就不能建模，只是落在区间之内建模效果比较好)。
Step2:
将原始数据时间序列进行累加生成
设累加生成之后的序列为X'Step3：
对累加生成之后的序列进行邻均值生成。
邻均值生成是对等时距数列，用相邻数据的平均值构造生成新的数据。
设新生成的邻均值序列为Z，则：
Z(k)=(X'(k)+X'(k+1))/2 ,k=1,2,…n
Step4:
构造数据矩阵B及数据向量Y
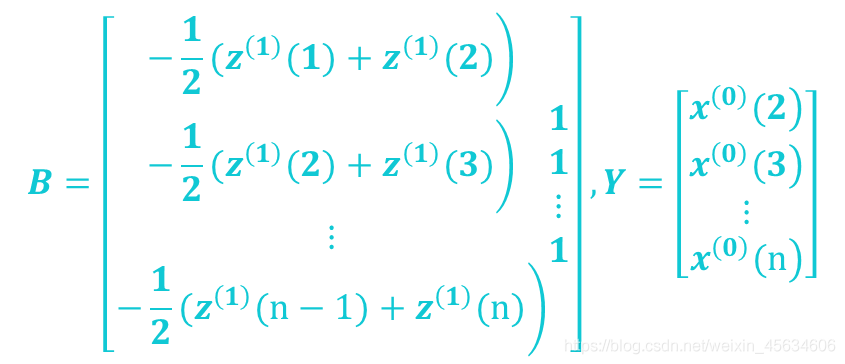Step5:
计算发展系数a及灰作用量b
计算方法如下：
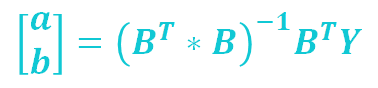
Step6：
建立模型求解时间响应函数并进行预测
GM(1，1)模型X(k)+aZ(k)=b的白化方程：
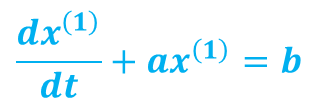
的时间响应函数为：
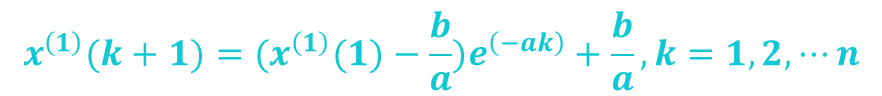
Step7：精确度检验
√相对残差检验
√方差比检验
√小误差概率检验
相对残差检验法：
设实际数据序列为X(k)
设模拟数据序列为X’(k)
则残差&为：
&(k)=X(k)-X‘(k)
相对误差*k=|&(k)|/X(k)
方差比检验法：
设残差序列为&(k)，其序列标准差为A。
原始序列为X(k)，其序列标准差为B。
则方差比C=A/B。
小误差概率检验法：
设小误差概率为p，残差序列平均值为&：P={|&(k)-&|<0.6745B}
则p=P/原始数据序列长度
小误差概率p及方差比检验标准(可在题目无要求精度时相对比较)
| 预测精度等级 | p(小误差概率) | C(方差比) |
|---|---|---|
| 一级 | >0.95 | <0.35 |
| 二级 | >0.8 | <0.5 |
| 三级 | >0.7 | <0.65 |
| 四级 | >0.6 | >=0.65(不合格) |
一般用作模型预测的话，精度等级要达到二级以上。
The End : MATLAB求解代码
clc;clear;
%建立符号变量a(发展系数)和b(灰作用量)
syms a b;
c = [a b]';
%原始数列
A = [174, 179, 183, 189, 207, 234, 220.5, 256, 270, 285];
%级比检验
n = length(A);
min=exp(-2/(n+1));
max=exp(2/(n+1));
for i=2:n
ans(i)=A(i-1)/A(i);
end
ans(1)=[];
for i=1:(n-1)
if ans(i)min
else
fprintf('第%d个级比不在标准区间内',i)
disp(' ');
end
end
%对原始数列 A 做累加得到数列 B
B = cumsum(A);
%对数列 B 做紧邻均值生成
for i = 2:n
C(i) = (B(i) + B(i - 1))/2;
end
C(1) = [];
%构造数据矩阵
B = [-C;ones(1,n-1)];
Y = A; Y(1) = []; Y = Y';
%使用最小二乘法计算参数 a(发展系数)和b(灰作用量)
c = inv(B*B')*B*Y;
c = c';
a = c(1);
b = c(2);
%预测后续数据
F = []; F(1) = A(1);
for i = 2:(n+10)
F(i) = (A(1)-b/a)/exp(a*(i-1))+ b/a;
end
%对数列 F 累减还原,得到预测出的数据
G = []; G(1) = A(1);
for i = 2:(n+10)
G(i) = F(i) - F(i-1); %得到预测出来的数据
enddisp('预测数据为：');
G
%模型检验
H = G(1:n);
%计算残差序列
epsilon = A - H;
%法一：相对残差Q检验
%计算相对误差序列
delta = abs(epsilon./A);
%计算相对误差平均值Qdisp('相对残差Q检验：')
Q = mean(delta)
%法二：方差比C检验
disp('方差比C检验：')
C = std(epsilon, 1)/std(A, 1)
%法三：小误差概率P检验
S1 = std(A, 1);
tmp = find(abs(epsilon - mean(epsilon))0.6745 * S1);
disp('小误差概率P检验：')
P = length(tmp)/n
%绘制曲线图
t1 = 1995:2004;
t2 = 1995:2014;
plot(t1, A,'ro'); hold on;
plot(t2, G, 'g-');
xlabel('年份'); ylabel('污水量/亿吨');
legend('实际污水排放量','预测污水排放量');
title('长江污水排放量增长曲线');
grid on;• end •
走在路上
goldsunC
